
此体系的应用条件是: (1)应力、应变满足虎克定律; (2)变形微小:变形前后结构尺寸、诸力作用位 置不变,位移计算可用叠加原理; (3)体系几何不变,约束为理想约束。 非线性体系: (1)物理非线性; (2)几何非线性(大变形)
非线性体系: (1) 物理非线性; (2)几何非线性(大变形)。 此体系的应用条件是: (1)应力、应变满足虎克定律; (2)变形微小:变形前后结构尺寸、诸力作用位 置不变,位移计算可用叠加原理; (3)体系几何不变,约束为理想约束

§9-2虚功和虚功原理 一、虚功 一个不变的力所做的功是以该力的大小与其作用 点沿力方向相应位移的乘积来衡量。 W=P△ (9-1) 把此式的定义扩大: 实功是力在自身引起的位移 上所作的功。 W一功,单位是Nm 虚功是力在虚位移上作的功。 P一力 如力与位移同向,虚功为正, 一与力相应的位移 反向时,虚功为负
§9-2 虚功和虚功原理 一、虚功 一个不变的力所做的功是以该力的大小与其作用 点沿力方向相应位移的乘积来衡量。 W=PΔ W —功,单位是N·m P—力 Δ —与力相应的位移 把此式的定义扩大: 实功是力在自身引起的位移 上所作的功。 虚功是力在虚位移上作的功。 如力与位移同向,虚功为正, 反向时,虚功为负。 (9-1)

1、广义力与广义位移 作功的两方面因素:力、位移。 与力有关的因素,称为广义力S。 与位移有关的因素,称为广义位移△。 广义力与广义位移的关系是:它们的乘积是虚功。 即:P△ 1)广义力是单个力,则广义位移是沿此力作用线 方向的线位移。 2)广义力是一个力偶,则广义位移是它所作用的 截面的转角B,即角位移
1、广义力与广义位移 作功的两方面因素:力、位移。 与力有关的因素,称为广义力S。 与位移有关的因素,称为广义位移Δ。 广义力与广义位移的关系是:它们的乘积是虚功。 即:W=PΔ 1)广义力是单个力,则广义位移是沿此力作用线 方向的线位移。 2)广义力是一个力偶,则广义位移是它所作用的 截面的转角β,即角位移
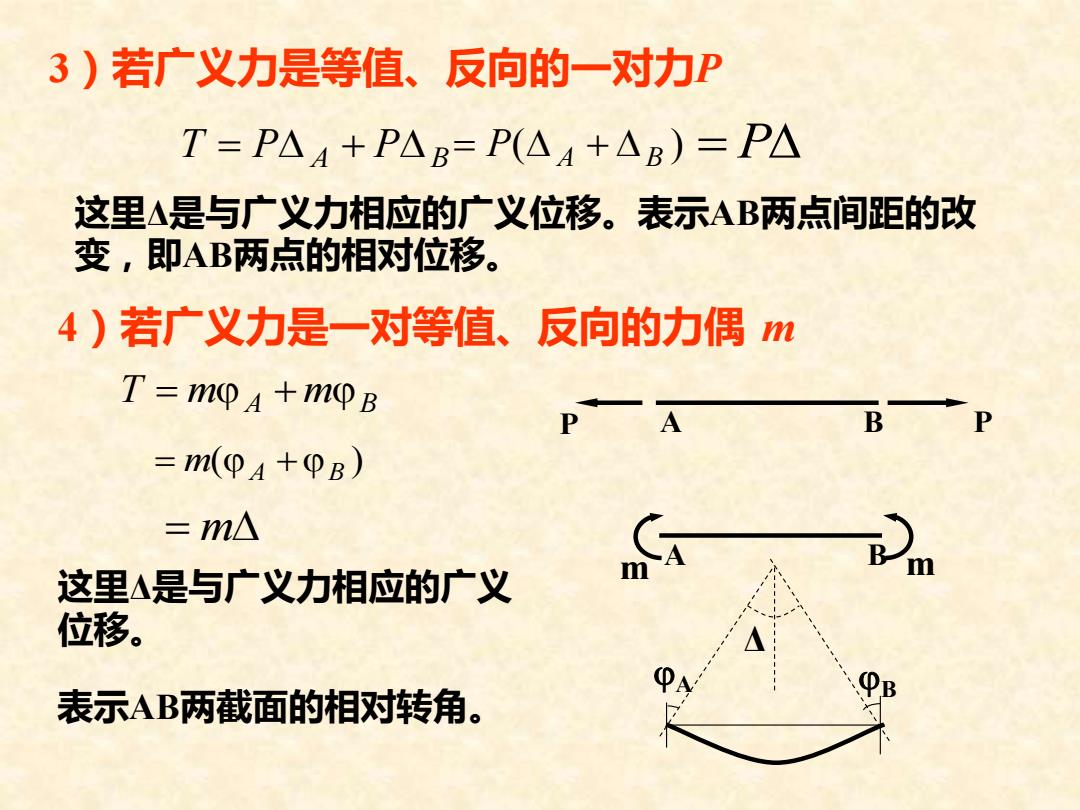
3)若广义力是等值、反向的一对力P T=PAA+P△B=P(AA+△B)=P△ 这里△是与广义力相应的广义位移。表示AB两点间距的改 变,即AB两点的相对位移。 4)若广义力是一对等值、反向的力偶m T=mopa+mB B P =m(+PB) =m△ 这里△是与广义力相应的广义 位移。 表示AB两截面的相对转角
3)若广义力是等值、反向的一对力P 这里Δ是与广义力相应的广义位移。表示AB两点间距的改 变,即AB两点的相对位移。 4)若广义力是一对等值、反向的力偶 m 这里Δ是与广义力相应的广义 位移。 表示AB两截面的相对转角。 T = PA + PB ( ) = P A + B = P T = m A + mB ( ) = m A +B = m P A B P m A B m Δ A B

2、虚功 为了与实功相区别,虚功的虚是指力作功的位移 不是由该力本身引起的,则: 作功的力与相应于力的位移彼此独立无关。 虚功=力×相应于力的位移 独立无关
2、虚功 为了与实功相区别,虚功的虚是指力作功的位移 不是由该力本身引起的,则: 作功的力与相应于力的位移彼此独立无关。 虚功 = 力 × 相应于力的位移 独立无关