
第 章 渐进法 近似法 及超静定结构的影响线
第 十 二 章 渐 进 法、近似法 及超静定结构的影响线

§12-1力矩分配法的基本概念 渐进法的提出 计算超静定刚架或连续梁,无论采用力法或 位移法,均需建立和求解线性代数方程组。当未知 量较多时,计算工作非常繁重,且在求得基本未知 量后,还要利用杆端弯矩叠加公式求得杆端弯矩。 有时几乎不可能完成。为此,提出了渐进法,以避 免解算联立方程组。 本章介绍: 1、力矩分配法 2、无剪力分配法、剪力分配法 3、超静定结构的近似法、超静定力的影响线
渐进法的提出 Ø 计算超静定刚架或连续梁,无论采用力法或 位移法, 均需建立和求解线性代数方程组。当未知 量较多时,计算工作非常繁重,且在求得基本未知 量后,还要利用杆端弯矩叠加公式求得杆端弯矩。 有时几乎不可能完成。为此,提出了渐进法,以避 免解算联立方程组。 Ø 本章介绍: Ø 1、力矩分配法。 Ø 2、无剪力分配法、剪力分配法 Ø 3、超静定结构的近似法、超静定力的影响线 §12-1 力矩分配法的基本概念

力矩分配法的基本概念 力矩分配法是渐进法的一种,是位移法 的变体,它是直接从实际结构的受力和变 形状态出发,根据位移法基本原理,从开 始建立的近似状态,逐步通过增量调整修 正,最后收敛于真实状态。适用范围是: 连续梁和无结点线位移的刚架 由于是以逐次渐进的方法来计算杆端 弯矩,其结果的精度随计算轮次的增加而 提高,最终收敛于精确解。 物理概念生动 形象,计算方法单一重复
• 力矩分配法是渐进法的一种,是位移法 的变体,它是直接从实际结构的受力和变 形状态出发,根据位移法基本原理,从开 始建立的近似状态,逐步通过增量调整修 正,最后收敛于真实状态。适用范围是: 连续梁和无结点线位移的刚架。 • 由于是以逐次渐进的方法来计算杆端 弯矩,其结果的精度随计算轮次的增加而 提高,最终收敛于精确解。物理概念生动 形象,计算方法单一重复。 力矩分配法的基本概念:
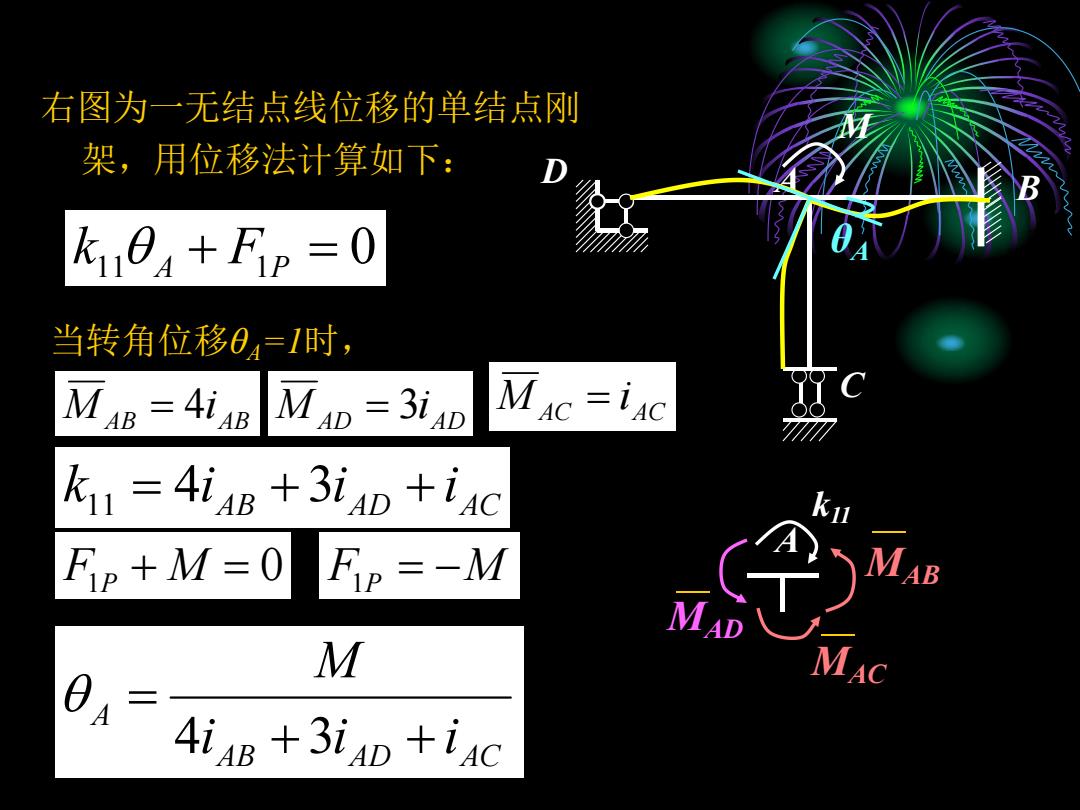
右图为一无结点线位移的单结点刚 架,用位移法计算如下: kuea+Fip =0 当转角位移04=1时, MAB=4iA8 MAD =3iAD Mic=iAc ku 4inB +3iap +iac Fip+M=0 Fip=-M VI AB AD M MAC 4iaB +3iap +iac
D A B C M θA A k11 MAB MAC MAD 右图为一无结点线位移的单结点刚 架,用位移法计算如下: 当转角位移θA=1时, 0 k11 A F1P AB AB M 4i AD AD M 3i AC AC M i AB AD AC k 4i 3i i 11 0 F1P M F1P M AB AD AC A i i i M 4 3
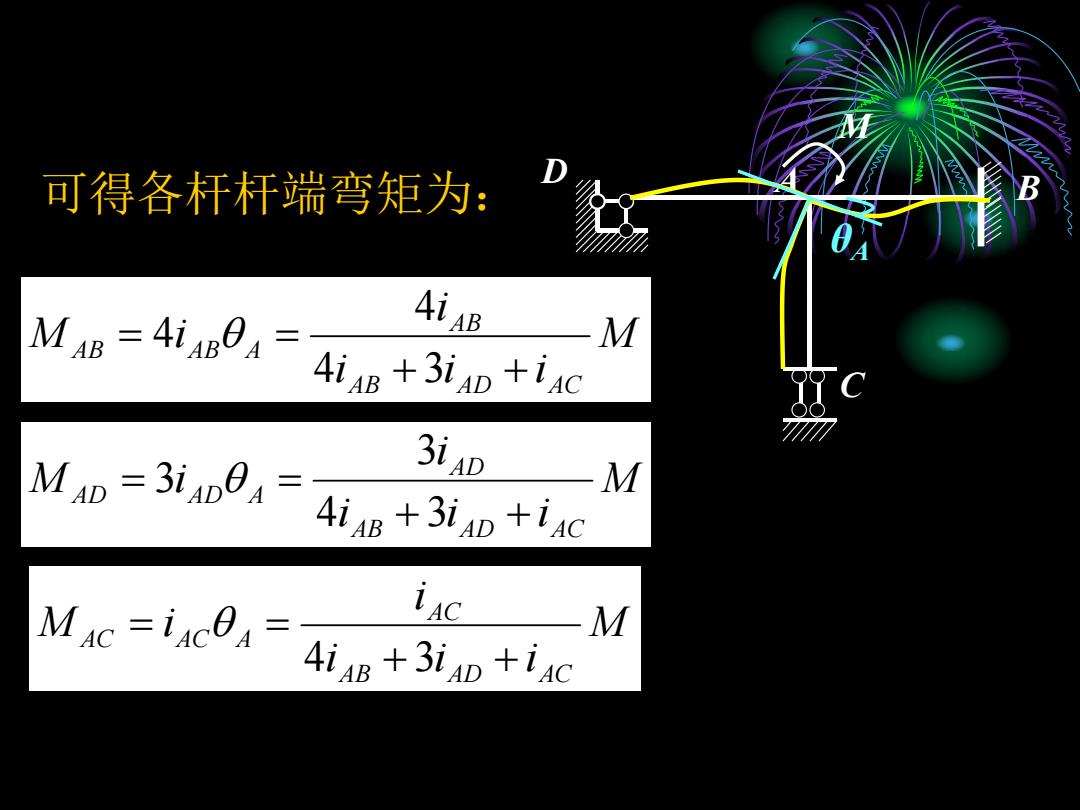
可得各杆杆端弯矩为: M in=4iAue AiAB -M 4iaB +3iap+iac MAD =3iAD0=2 3iAD -M 4iaB +3iap +iac MAc =ince= LAC M 4iaB +3iaD +iac
D A B CMθA 可得各杆杆端弯矩为: M i i i i M i AB AD AC AB AB AB A 4 34 4 M i i i i M i AB AD AC AD AD AD A 4 33 3 M i i i i M i AB AD AC AC AC AC A 4 3