
12-2 二项分布 (1)适用条件 车辆比较拥挤、自由行驶机 会不多的车流
二项分布 • 车辆比较拥挤、自由行驶机 • 会不多的车流。 (1) 适用条件

2-2 二项分布 Pk一在计数间隔内到达k辆车的 (2)基本公式 概率; -c0产y 平均到车率(辆/S); t一每个计数间隔持续的时间(s) 之 n一正整数,观测间隔t内可能到 k=0,1,2,.n 达的最大车辆数。 p=人tn一辆车到达的概率 P=Cp*(I-p)”-
二项分布 k=0,1,2,.n Pk一在计数间隔t内到达k辆车的 概率; λ一平均到车率(辆/s); t一每个计数间隔持续的时间(s) n一正整数,观测间隔t内可能到 达的最大车辆数。 k k n k k n n t n t P C ( ) (1 ) k k n k Pk Cn p p (1 ) p=λt/n 一辆车到达的概率 (2) 基本公式
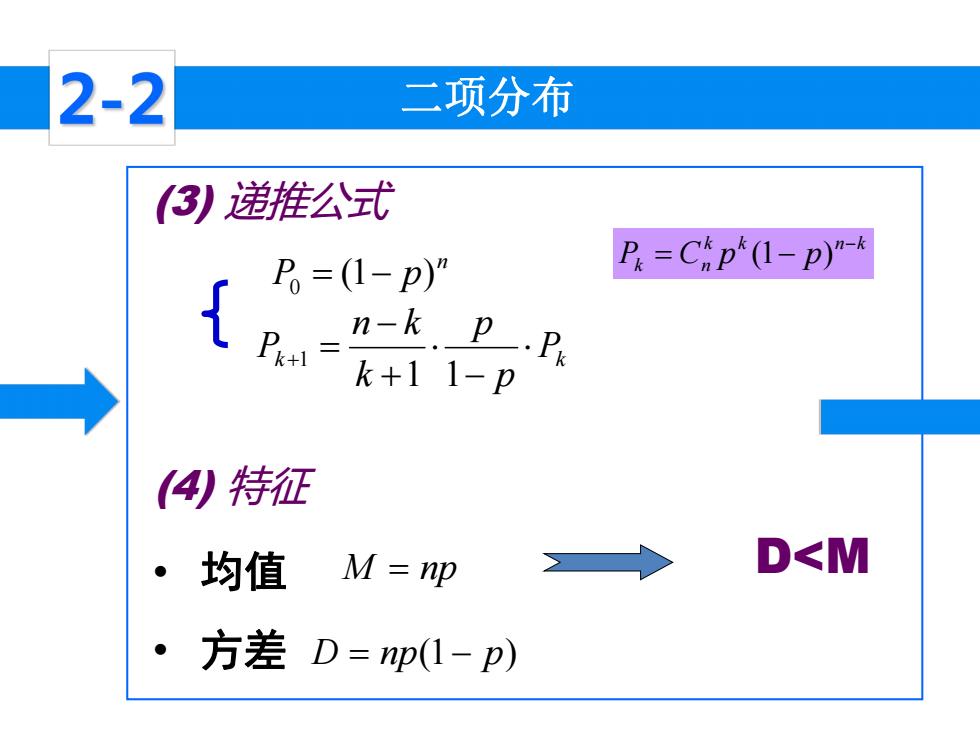
2-2 二项分布 (3递推公式 P=(1-p)” P.=Ckp*(1-p)"-k n-k p.P k+11-p 4)特征 。均值 M=np D<M 方差D=np(1-p)
二项分布 (3) 递推公式 • 均值 • 方差 (4) 特征 n P (1 p) 0 k Pk p p k n k P 1 1 1 k k n k Pk Cn p p (1 ) M np D np(1 p) D<M
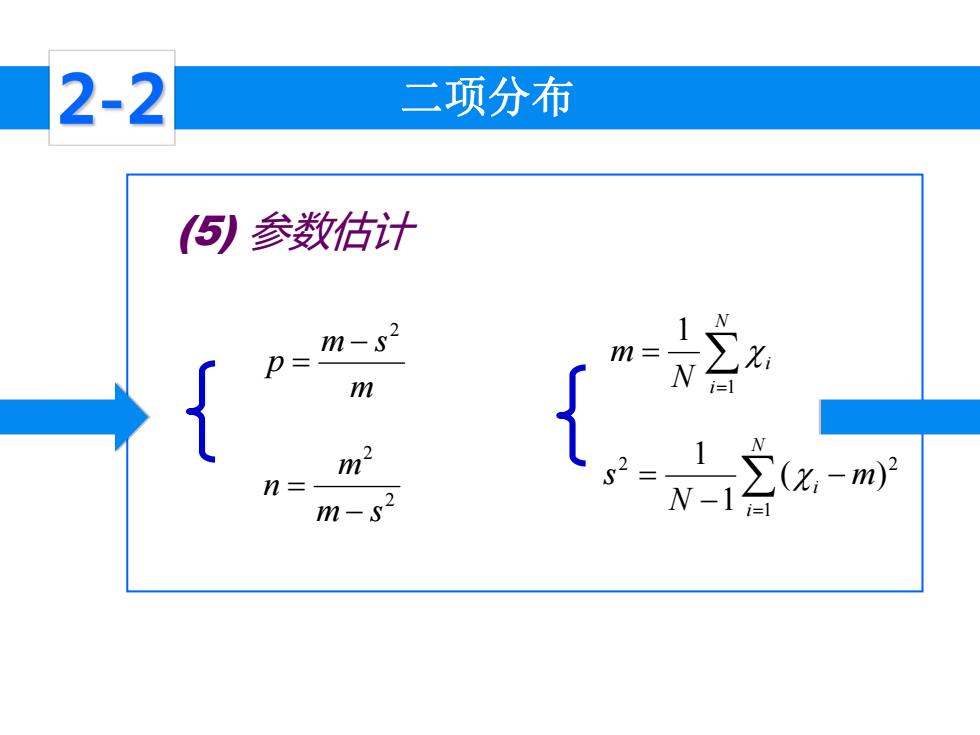
2-2 二项分布 ⑤参数估计 m-2 m n= m-s2
二项分布 (5) 参数估计 m m s p 2 2 2 m s m n N i i N m 1 1 N i i m N s 1 2 2 ( ) 1 1

【例4-3】以15s间隔观测到达车辆数,得到结果。 车辆到达数ns <3 3 4 5 6 8 9 10 1112>12 包含ns间隔 出现的次数 0 3 0 8 101110 11 9 0 解:m= 3×3+4×0+.+12×1 =7.469 3+0+.+1 -8以区xw=3 p=(7.469-3.999)/7.469=0.465 n=m/D=7.469/0.465=16.08
【例4-3】以15s间隔观测到达车辆数,得到结果。 解: 7.469 3 0 . 1 1 3 3 4 0 . 12 1 1 N i i N m ( ) 3.999 1 1 ( ) 1 1 1 2 2 1 2 2 N i i N i i Nm N m N s p (7.469 3.999)/ 7.469 0.465 n m / D 7.469 / 0.465 16.08