2-1 泊松分布 计数间隔内 3递推公式 平均到达的 车辆数 (At)e-a m=At Po=e-m I P m Px =k+l 4特征 分布的均值M和方差D都等于入t
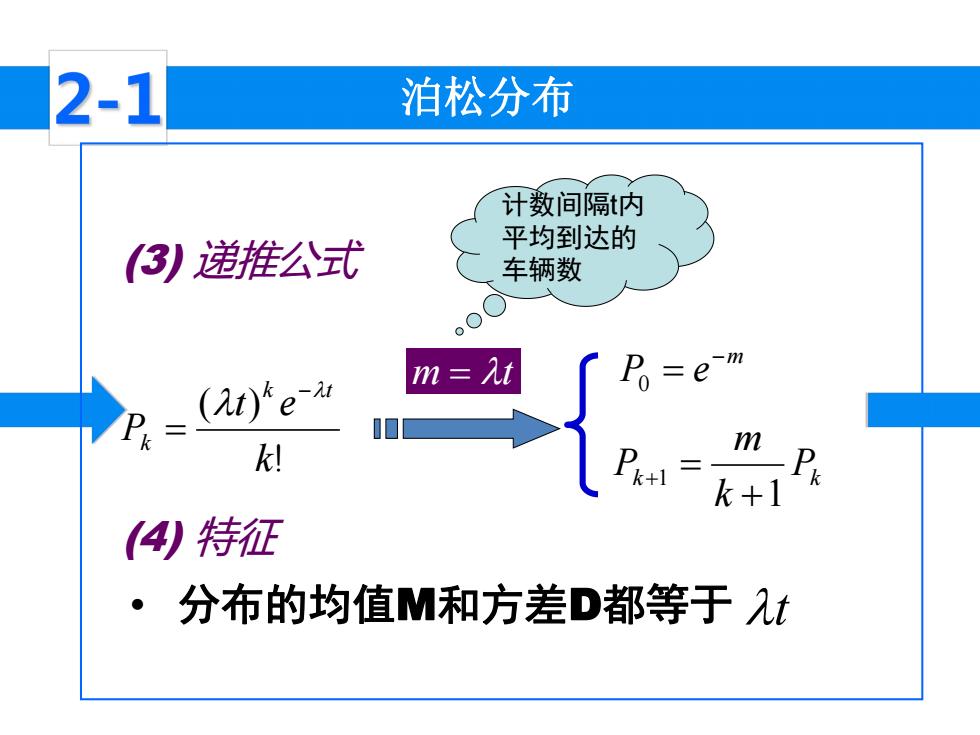
泊松分布 (3) 递推公式 ! ( ) k t e P k t k m P e 0 k Pk k m P 1 1 m t • 分布的均值M和方差D都等于 (4) 特征 t 计数间隔t内 平均到达的 车辆数

【例4-1】设60辆车随机分布在4km长的道路上,服 从泊松分布,求任意400米路段上有4辆及4辆车以上 的概率。 解:t=400m,λ=60/4000辆/m,m=λt=6 辆 60 e6=0.0025: P= 6 ,P。=0.01 0+1 6 6 P2= P=0.0446; 1+1 P3= P2=0.0892 2+1 不足4辆车的概率:P(k<4)=号P=0.1512 i=0 4辆及4辆以上的概率:P(k>=4)=1-P(k<4)=0.8488
【例4-1】设60辆车随机分布在4km长的道路上,服 从泊松分布,求任意400米路段上有4辆及4辆车以上 的概率。 解:t=400 m,λ=60/4000 辆/m,m=λt=6 辆
【例4-2】Adams数值例题 ·对某一交叉口观测数据如下 10S周期车辆到达数 观测频次 总观测车辆数 泊松拟合频率 0 94 0 63 63 2 21 42 3 2 6 〉3 0 0 合计 180 111
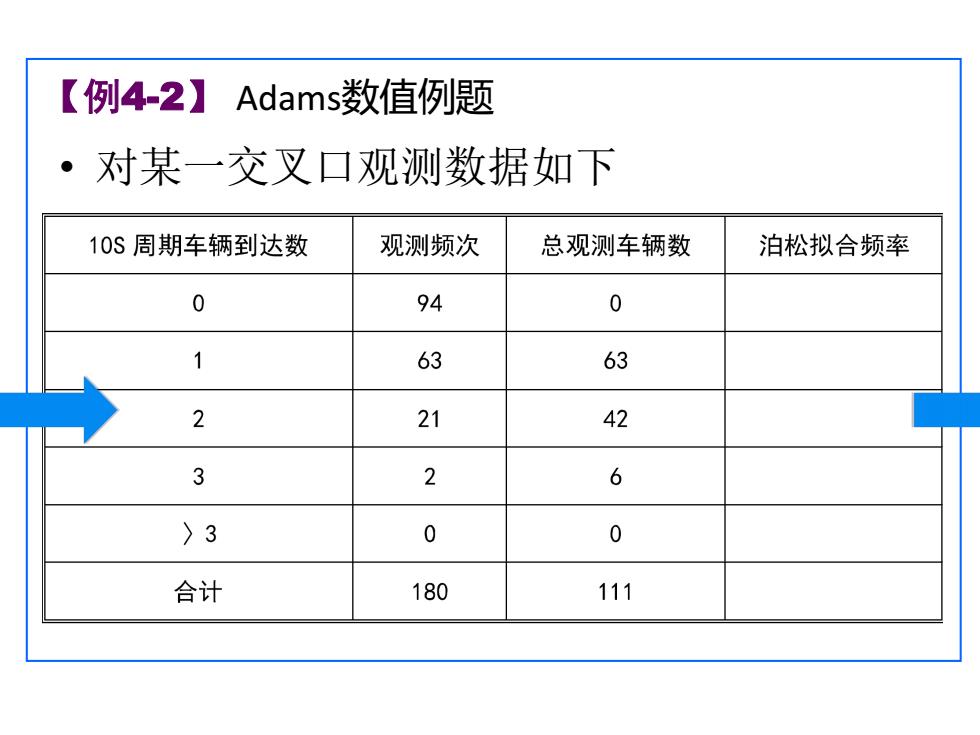
【例4-2】 Adams数值例题 • 对某一交叉口观测数据如下

解:t=10s,λ=111/(180*10) 辆m, m=λt=0.617 0=em=0.5397 ?=mP=0.3328 →=P=0.1026=m=0.0211 m m 2 3 P(3)=1-P≤3)=1-∑乃 =1-(P+P+P+P)=0.0037
解:t=10s,λ=111/(180*10) 辆/m, m=λt=0.617 0 0.5397 m P e P1 mP0 0.3328 0.1026 2 2 P1 m P 0.0211 3 3 P2 m P 1 ( ) 0.0037 ( 3) 1 ( 3) 1 0 1 2 3 3 0 P P P P P P P k i

【例43】某信号灯交叉口的周期C=97s,有效绿灯 时间g=44s,在有效绿灯时间内排队的车流以 s=900(辆)的交通量通过交叉口,在有效绿灯时 间外到达的车辆要停车排队。设信号灯交叉口上游车 辆的到达率g=369(辆h),服从泊松分布,求到达 车辆不至于两次排队的周期数占周期总数的最大百分 率
【例4-3】某信号灯交叉口的周期C =97s,有效绿灯 时间g =44s,在有效绿灯时间内排队的车流以 s=900(辆/h)的交通量通过交叉口,在有效绿灯时 间外到达的车辆要停车排队。设信号灯交叉口上游车 辆的到达率q=369(辆/h),服从泊松分布,求到达 车辆不至于两次排队的周期数占周期总数的最大百分 率