
二、单个参数的假设检验:t检验 2、关于单侧备择假设的检验 ,除了零假设外,我们需要替代假设H,并设定显著性水平 ,H,可以是单边或双边的 H:P>0和H:B<0是单边的 H:B≠0是双边替代假设 ,显著水平为5%意味着,当Ho实际上正确时拒绝它的概率,错误地拒绝实 际上为真的零假设的概率是5%。 y 当备择假设H:月>0下,tg期望值为正。寻找一个足够大的正值,可以 拒绝Ho ,检验步骤: ①取定显著性水平a后,找到自由度为n-k-I的t分布的处于(I-)百分数的数值c,即 临界值 ②若t>c(拒绝法则),则在显著水平a下,t统计量足够大,应拒绝原假 设。此时错误拒绝原假设的概率为 16 中级计量经济学
二、单个参数的假设检验:t检验 2、关于单侧备择假设的检验 除了零假设外,我们需要替代假设H1,并设定显著性水平 H1可以是单边或双边的 H1 : j > 0 和 H1 : j < 0 是单边的 H1 : j 0是双边替代假设 显著水平为5%意味着,当H0实际上正确时拒绝它的概率,错误地拒绝实 际上为真的零假设的概率是5%。 当备择假设H1:j > 0下, 𝑡𝛽𝑗期望值为正。寻找一个足够大的正值,可以 拒绝H0 检验步骤: 取定显著性水平a后,找到自由度为n – k – 1的t分布的处于(1 – a)百分数的数值c,即 临界值 若𝑡𝛽𝑗 > 𝑐(拒绝法则),则在显著水平𝛼下,t统计量足够大,应拒绝原假 设。此时错误拒绝原假设的概率为𝛼 16 中级计量经济学
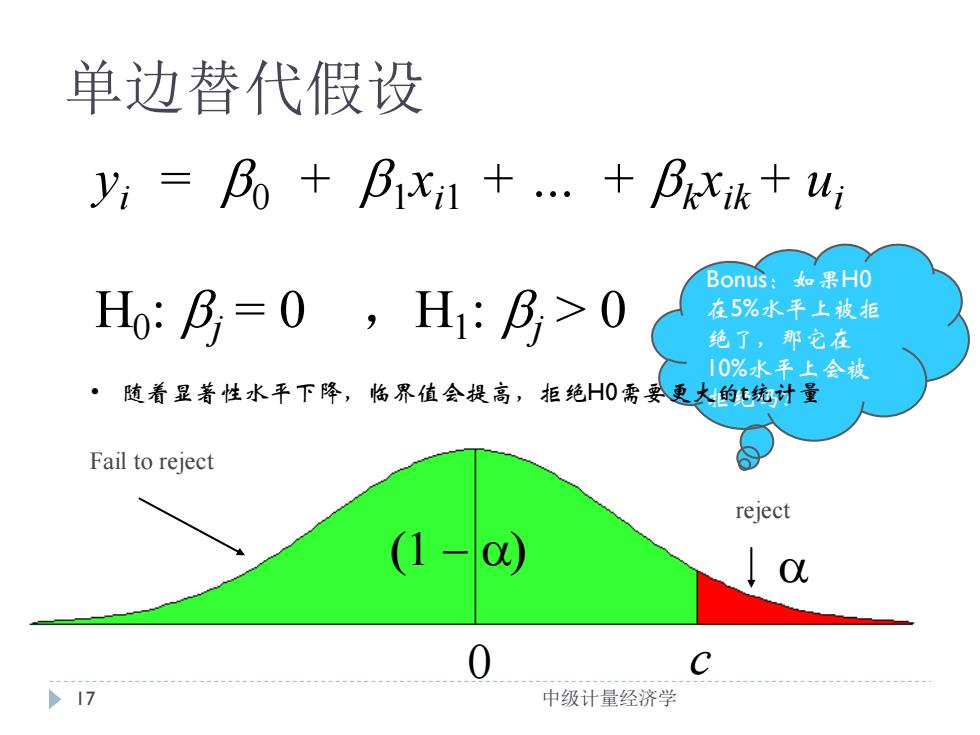
单边替代假设 y:=B+B1x1+.+Bxk+u Bonus:k如果H0 Ho:=0,H:B,>0 在5%水平上被拒 绝了,那它在 10%水平上会被 随着显著性水平下降,临界值会提高,拒绝H0需要更太的计量 Fail to reject reject C >17 中级计量经济学
17 中级计量经济学 yi = 0 + 1 xi1 + . + k xik+ ui H0 : j = 0 ,H1 : j > 0 0 c a (1 − a) 单边替代假设 Fail to reject reject Bonus:如果H0 在5%水平上被拒 绝了,那它在 10%水平上会被 • 随着显著性水平下降,临界值会提高,拒绝H0需要更大的拒绝吗? t统计量

二、单个参数的假设检验:t检验 One-Sided Alternatives >如果H月=0,H1:月,>0, 当,>C时拒绝H,当ta,≤C,则不能拒绝H 如果HoB=0,H1:乃<0,当 t元,<-C时拒绝,当t2,≥-C,则不能拒绝H。 >I8 中级计量经济学
18 中级计量经济学 One-Sided Alternatives 如果H0 : j = 0,H1 : j > 0, 当 时拒绝H0,当 ,则不能拒绝H0 如果H0 : j = 0,H1 : j < 0,当 时拒绝H0,当 ,则不能拒绝H0 ˆ j t c ˆ j t c ˆ j t c − ˆ j t c − 二、单个参数的假设检验:t检验
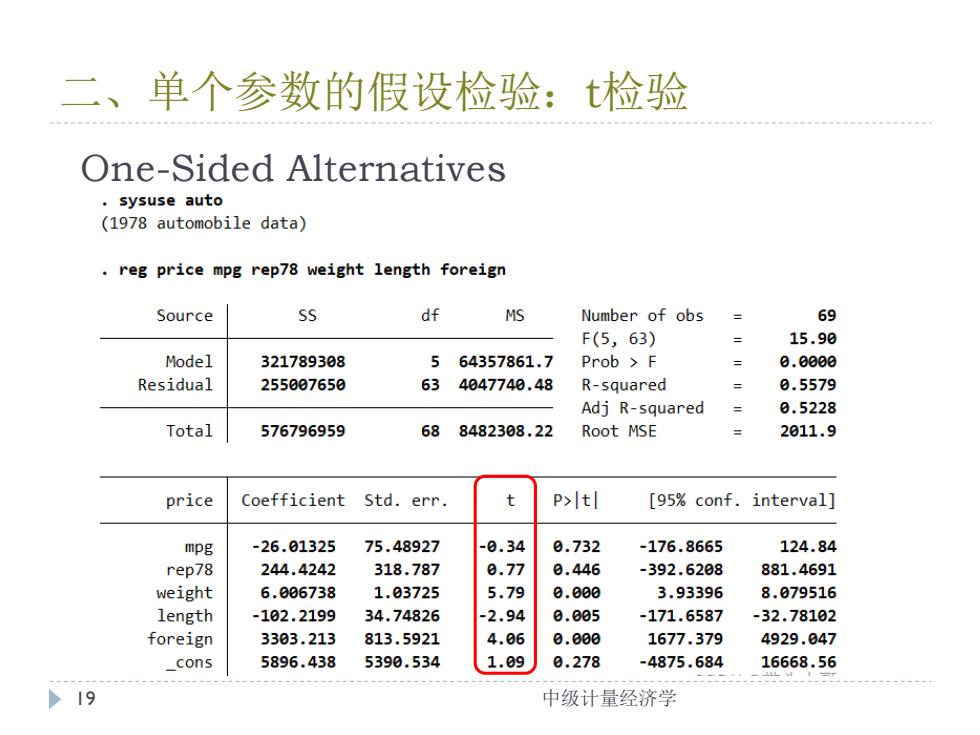
二、单个参数的假设检验:t检验 One-Sided Alternatives sysuse auto (1978 automobile data) reg price mpg rep78 weight length foreign Source SS df MS Number of obs 69 F(5,63) 15.90 Model 321789308 64357861.7 Prob F 0.0000 Residual 255097650 63 4047740.48 R-squared 0.5579 Adj R-squared = 0.5228 Total 576796959 68 8482308.22 Root MSE 2011.9 price Coefficient Std.err. t P>ltl [95%conf.interval] mpg -26.01325 75.48927 -0.34 0.732 -176.8665 124.84 rep78 244.4242 318.787 0.77 0.446 -392.6208 881.4691 weight 6.006738 1.83725 5.79 0.800 3.93396 8.879516 length -102.2199 34.74826 -2.94 0.805 -171.6587 -32.78102 foreign 3303.213 813.5921 4.06 0.000 1677.379 4929.847 _cons 5896.438 5390.534 1.09 0.278 4875.684 16668.56 19 中级计量经济学
19 中级计量经济学 One-Sided Alternatives 如果H0 : j = 0,H1 : j > 0, 当 时拒绝H0,当 ,则不能拒绝H0 如果H0 : j = 0,H1 : j < 0,当 时拒绝H0,当 ,则不能拒绝H0 ˆ j t c ˆ j t c ˆ j t c − ˆ j t c − 二、单个参数的假设检验:t检验

二、单个参数的假设检验:检验 例子 例↓.1国 小时工资方程 使用WAGE1中的数据得到如下估计方程: log(age)=0.284+0.092edue+0.004 -0.022tenure (0.104)(0.007) (0.00 (0.003) n=526,R2=0.316 其中,标准误被标在了估计参数下面的括号中,我们以后在全书中都采用这一做法。这个方程可用来检验, 在控制了educ和tenure的情况下,总体中exper的回报是否为零,以正回报为备择假设。可以写成H: 民m=0对H:Rm>0。(在应用中,用相应变量名称做参数的下标是一个很好的方法,因为我们在一般模 型中,用数字指标作为下标很随意,而且容易导致混淆。)记住,R表示未知总体参数。写“H:0.0041= 0”或“H:序加=0”都毫无意义。 因为我们有522个自由度,所以我们可以使用标准正态临界值。显著性水平为5%的临界值是1.645,显 著性水平为1%的临界值是2.326.3的t统计量是 txm=0.0041/0.0017≈2.41 所以,m或expr即使在%的显者性水平上都是统计显著的。我们还说:“在16的显著性水平上,Bm 是统计显著大于零的”。 保持现职任期和受教育程度不变,多一年工作经历的估计回报并不大。比如,增加3年工作经历使 log(ug)提高3X0.0041=0,0123,所以工资只高出1.2%。不过,我们还是颜有说服力地证明了,总体学 中工作经历的偏效应是正的
二、单个参数的假设检验:t检验 例子 20 中级计量经济学