
OLS估计量的抽样分布 我们已经知道当Gauss一Markov假设成立时,OLS是 最优线性无偏估计(BLUEs)。 ,为了进行经典的假设检验,我们要在Gauss一 Markov假设之外增加另一假定。为了使的抽样分布 易于处理,对总体中不可观测的误差项的分布进行 假定。 ,假定MLR.6(正态性):假设总体误差u独立于解 释变量x,2,×k,且u服从均值为0,方差为62的正 态分布。 6 中级计量经济学
一、 OLS估计量的抽样分布 6 中级计量经济学 我们已经知道当Gauss-Markov假设成立时,OLS是 最优线性无偏估计(BLUEs)。 为了进行经典的假设检验,我们要在Gauss- Markov假设之外增加另一假定。为了使的抽样分布 易于处理,对总体中不可观测的误差项的分布进行 假定。 假定MLR.6 (正态性):假设总体误差u独立于解 释变量x1 , x2 ,., xk,且u服从均值为0,方差为 2的正 态分布
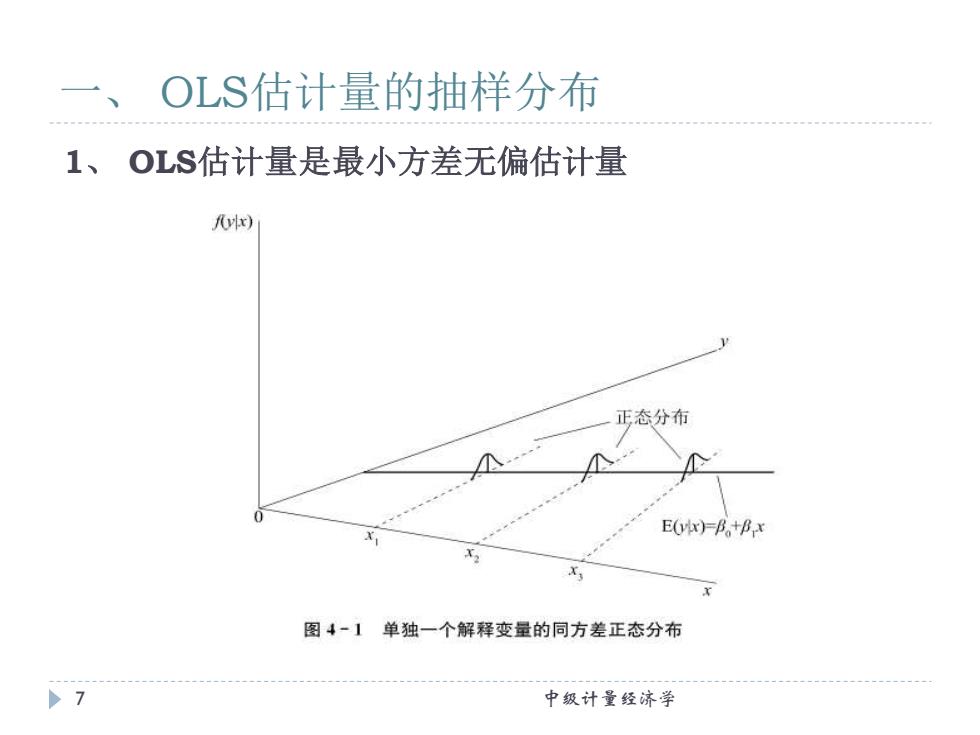
一、OLS估计量的抽样分布 1、OLS估计量是最小方差无偏估计量 fvx) 正态分布 E(vix)-B+Bx 图4-1单独一个解释变量的同方差正态分布 中级计量经济学
1、 OLS估计量是最小方差无偏估计量 一、 OLS估计量的抽样分布 7 中级计量经济学

OLS估计量的抽样分布 ,假设MLR6更强,当MLR6成立时,则必然假定了MLR4和 MLR.5 假设MLR.I-MLR.6被称为经典线性模型假定 ,将满足这六个假定的模型称为经典线性模型(CLM) ylx Normal(Bo+B x1+.+Bxk o2) 以x为条件的y服从正态分布,该分布的均值线性于x的取 值,方差为常数。 ,在经典线性模型假设下,OLS不仅是BLUE,而且是最小方差 无偏估计量,即在所有线性和非线性的估计量中,OLS估计 量具有最小的方差。 中级计量经济学
8 中级计量经济学 一、 OLS估计量的抽样分布 假设MLR.6更强,当MLR.6成立时,则必然假定了MLR.4和 MLR.5 假设MLR.1-MLR.6被称为经典线性模型假定 将满足这六个假定的模型称为经典线性模型(CLM) y|x ~ Normal(0 + 1 x1 +.+ k xk ,2 ) 以x为条件的y服从正态分布,该分布的均值线性于x的取 值,方差为常数。 在经典线性模型假设下,OLS不仅是BLUE,而且是最小方差 无偏估计量,即在所有线性和非线性的估计量中,OLS估计 量具有最小的方差

OLS估计量的抽样分布 1、OLS估计量是最小方差无偏估计量 根据对总体的经典线性模型假设有: 、有截新持征 D ylx Normal(Bo+Bix+.+Bxk,2) 如收入 为什么或者是否可以假设误差服从正态分 2、离散变量, 有很多0值肘, o2)? 虚拟变量等 ,现实中存在不符合该假设的例子?Y的分布 如果正态假设不成立怎么办? 通过变换,特别是通过取自然对数,往往可以 得到接近于正态的分布。大样本允许我们放弃 正态假设(近似方式) 9 中级计量经济学
根据对总体的经典线性模型假设有: y|x ~ Normal(0 + 1 x1 +.+ k xk , 2 ) 为什么或者是否可以假设误差服从正态分布,u~Normal(0, 2 )? 现实中存在不符合该假设的例子?Y的分布 9 中级计量经济学 1、 OLS估计量是最小方差无偏估计量 一、 OLS估计量的抽样分布 如果正态假设不成立怎么办? 通过变换,特别是通过取自然对数,往往可以 得到接近于正态的分布。大样本允许我们放弃 正态假设(近似方式) 1、有截断特征, 如收入 2、离散变量, 有很多0值时, 虚拟变量等

OLS估计量的抽样分布 误差服从正态分布→OLS估计量的正态抽样分布 定理4.1正态抽样分布 B=目 Var(Bi)=? 在CLM假设下,条件于解释变量 本值有,月Normal[B,ar(B,)】],故 (B,-,)/ (a】Nom()) 标准正态随机变量 B服从正态分布,因为它是误差的线性组合 >10 中级计量经济学
10 中级计量经济学 定理4.1 正态抽样分布 ( ) ( ) ( ) ( ) j CLM ˆ ~ Normal , , ˆ ˆ ~ Normal 0,1 ˆ ˆ j j j j j j Var sd − 在 假设下,条件于解释变量的样 本值有 故 服从正态分布,因为它是误差的线性组合 误差服从正态分布→OLS估计量的正态抽样分布 一、 OLS估计量的抽样分布 𝛽 𝑗 =? Var(𝛽 𝑗 ) =? 标准正态随机变量