第六章共形映射 历安毛子代枚大学 XIDIAN UNIVERSITY Conformal mapping y (W 相交于点z的任何两条曲线C,与C,之间的夹角,在其大小和方向上都等同 于经w=fz)映射后C,与C,对应的曲线厂与,之间的夹角,所以这种映射具有 保持两曲线间夹角与方向不变的性质.这种性质称为保角性。 场论与复变函数Field Theory and Complex Variable Functions 12
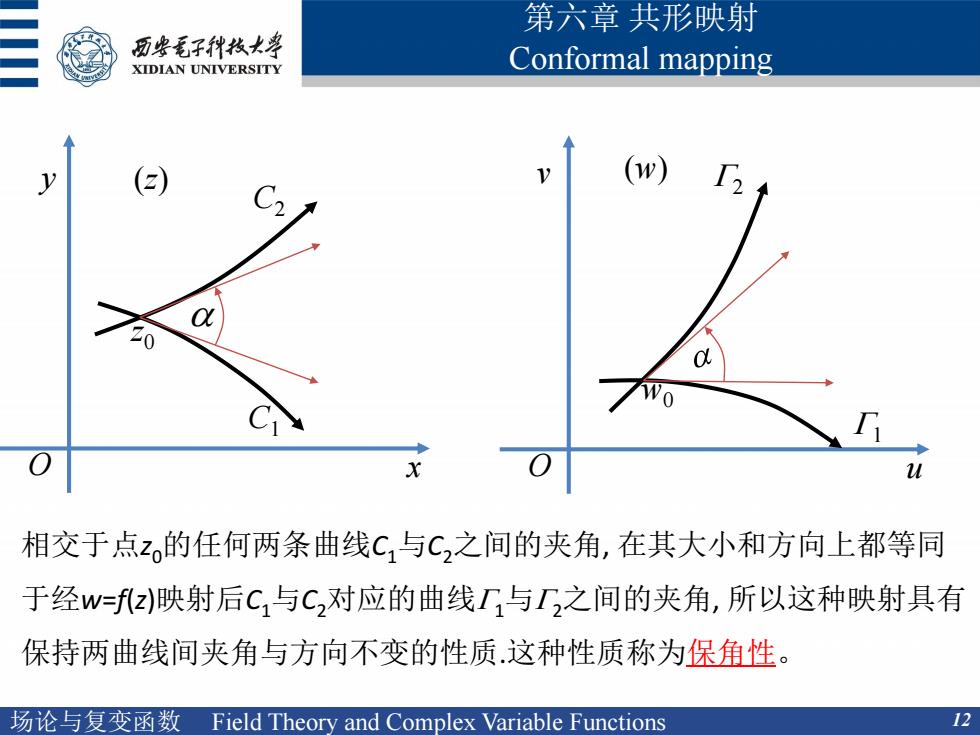
场论与复变函数 Field Theory and Complex Variable Functions 12 第六章 共形映射 Conformal mapping 相交于点z0的任何两条曲线C1与C2之间的夹角, 在其大小和方向上都等同 于经w=f(z)映射后C1与C2对应的曲线G1与G2之间的夹角, 所以这种映射具有 保持两曲线间夹角与方向不变的性质.这种性质称为保角性。 O x y O u (z) v (w) z0 w0 a C1 C2 G1 G2

第六章共形映射 历安毛子代枚大等 XIDIAN UNIVERSITY Conformal mapping (z) W u peid △σp A 另由: w-wo f(z)-f(zo) eo-9 Z-Zo Z-Zo reig △s△o △G 得: lf'(zo1=1imlf'(zo)川 lw -wol lim 7→Z0 Iz-zol z2015 (6.1.2) f(zo)川称为曲线C在z的伸缩率 场论与复变函数Field Theory and Complex Variable Functions 13
场论与复变函数 Field Theory and Complex Variable Functions 13 第六章 共形映射 Conformal mapping |f ‘(z0 )|称为曲线C在z0的伸缩率. O x y O u v z0 P0 r z P Ds C (z) (w) G w0 Q0 Q w r Dσ 另由: 得: (6.1.2)

第六章共形映射 面些毛子种枚大票 XIDIAN UNIVERSITY Conformal mapping (6.1.2)表明:f(z川是经过映射w=f孔z)后通过z点的任意曲线C 在z的伸缩率,它与曲线C的形状及方向无关。所以当f'(z≠0 时,映射w=fz)在zo点具有伸缩率不变性 场论与复变函数Field Theory and Complex Variable Functions 14
场论与复变函数 Field Theory and Complex Variable Functions 14 第六章 共形映射 Conformal mapping (6.1.2)表明: |f ‘(z)|是经过映射w=f(z)后通过z0点的任意曲线C 在z0的伸缩率, 它与曲线C的形状及方向无关。所以当f ’(z0 )0 时,映射w=f(z)在 z0点具有伸缩率不变性

第六章共形映射 历些毛子代找大学 XIDIAN UNIVERSITY Conformal mapping 定理一 设函数w=f孔z)在区域D内解析,z为D内的一点,且f《z≠0,则映 射w=f孔z)在Z具有两个性质: 1)保角性.即通过z的两条曲线间的夹角跟经过映射后所得两 曲线间的夹角在大小和方向上保持不变: 2)伸缩率不变性.即通过z的任何一条曲线的伸缩率均为 f'(z川,而与其形状和方向无关, 场论与复变函数Field Theory and Complex Variable Functions 15
场论与复变函数 Field Theory and Complex Variable Functions 15 第六章 共形映射 Conformal mapping 定理一 设函数w=f(z)在区域D内解析, z0为D内的一点, 且f ‘(z0 )0, 则映 射w=f(z)在z0具有两个性质: 1)保角性. 即通过z0的两条曲线间的夹角跟经过映射后所得两 曲线间的夹角在大小和方向上保持不变; 2)伸缩率不变性. 即通过z0的任何一条曲线的伸缩率均为 |f ’(z0 )|,而与其形状和方向无关

第六章共形映射 历些毛子种枚大票 XIDIAN UNIVERSITY Conformal mapping 3.共形映射的概念 定义设映射w=fz)在z,的邻域内是一一对应的,且Argf'(zo表 示这个映射在z的转动角,f'(zo川表示在z的伸缩率,在zo具有 保角性和伸缩率不变性,则称映射w=f孔z)在zo是共形的,或称 w=f孔z)在z是共形映射.如果映射w=fz)在D内的每一点都是共 形的,就称w=f孔z)是区域D内的共形映射 场论与复变函数Field Theory and Complex Variable Functions 16
场论与复变函数 Field Theory and Complex Variable Functions 16 第六章 共形映射 Conformal mapping 3. 共形映射的概念 定义 设映射w=f(z)在z0的邻域内是一一对应的, 且Arg f ‘(z0 )表 示这个映射在z0的转动角, |f ’(z0 )|表示在z0的伸缩率, 在z0具有 保角性和伸缩率不变性, 则称映射w=f(z)在z0是共形的, 或称 w=f(z)在z0是共形映射. 如果映射w=f(z)在D内的每一点都是共 形的, 就称w=f(z)是区域D内的共形映射