
第六章共形映射 历安毛子代枚大等 XIDIAN UNIVERSITY Conformal mapping 定理二如果函数w=f孔z)在z,解析,且f(zo0,则映射w=fz)在zo 是共形的。如果解析函数w=f孔z)在D内处处有f'(z)≠0,则映射 w=f孔z)是D内的共形映射。 场论与复变函数Field Theory and Complex Variable Functions
场论与复变函数 Field Theory and Complex Variable Functions 17 第六章 共形映射 Conformal mapping 定理二 如果函数w=f(z)在z0解析, 且f ‘(z0 )0, 则映射w=f(z)在z0 是共形的。如果解析函数w=f(z)在D内处处有f ’(z)0, 则映射 w=f(z)是D内的共形映射
第六章共形映射 历安毛子代枚大学 XIDIAN UNIVERSITY Conformal mapping y () 1 (w) C 2 0 定理二的几何意义:在D内作以z为其一个顶点的小三角形,在映射 下,得到一个以w为其一个顶点的三角形,这两个三角形对应边长 之比为f(z川,有一个角相等,则这两个三角形相似. 场论与复变函数Field Theory and Complex Variable Functions 18
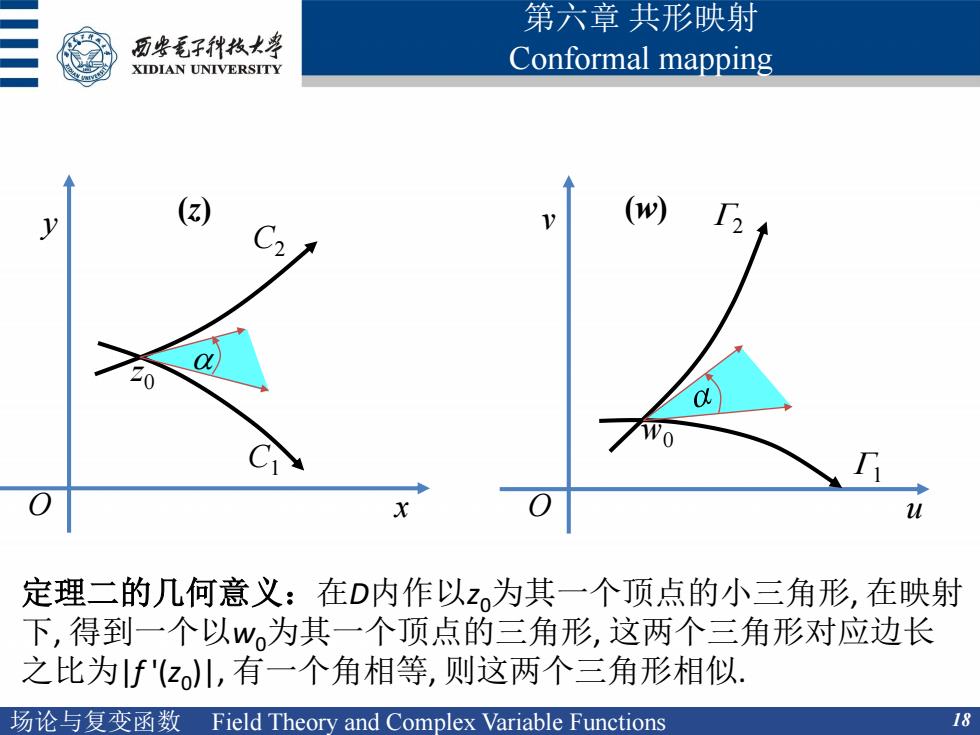
场论与复变函数 Field Theory and Complex Variable Functions 18 第六章 共形映射 Conformal mapping 定理二的几何意义:在D内作以z0为其一个顶点的小三角形, 在映射 下, 得到一个以w0为其一个顶点的三角形, 这两个三角形对应边长 之比为|f '(z0 )|, 有一个角相等, 则这两个三角形相似. O x y O u v (z) (w) z0 w0 a C1 C2 G1 G2
第六章共形映射 历安毛子代枚大学 XIDIAN UNIVERSITY Conformal mapping (w) ( 伸缩率f'(2)1≈ w-wol 由此看出映射w=f(Z)也将很小 lz-zol 的圆z-zo=δ,近似地映射成圆w-wo=|f'(zo)川6。 场论与复变函数Field Theory and Complex Variable Functions 19
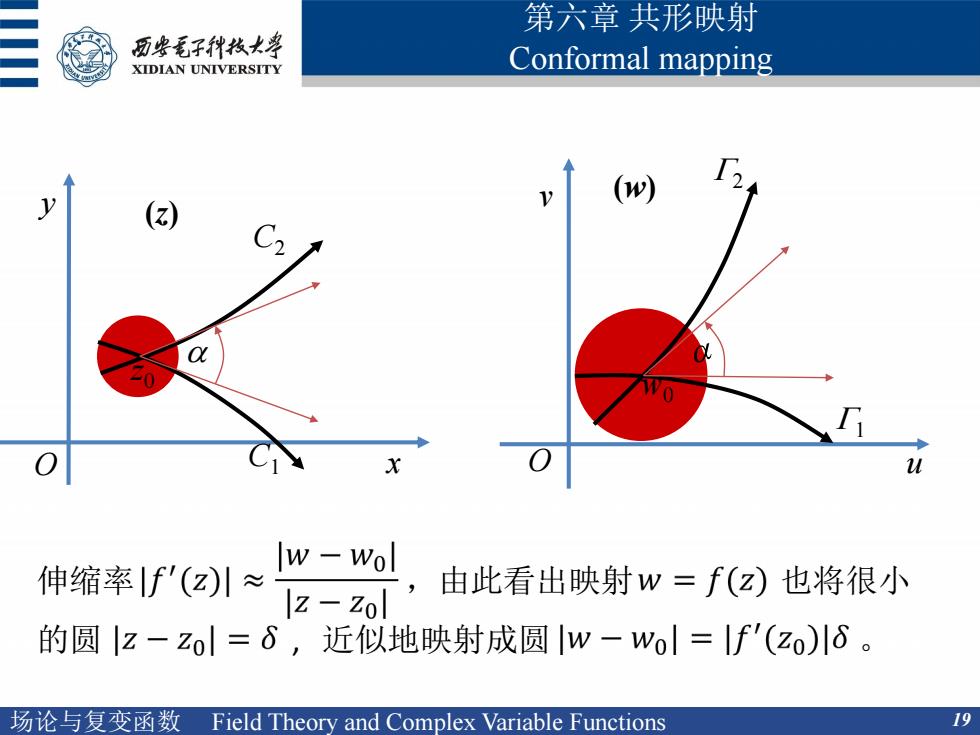
场论与复变函数 Field Theory and Complex Variable Functions 19 第六章 共形映射 Conformal mapping O x y O u v (z) (w) z0 w0 a C1 C2 G1 G2 伸缩率 ,由此看出映射 也将很小 的圆 , 近似地映射成圆

第六章共形映射 历些毛子代枝大学 XIDIAN UNIVERSITY Conformal mapping 第二节 分式线性映射 分式线性映射+名 cz+d 是一种常用的映 射,它可以看成由3种基本映射符合而成,在映射过程中具有 保角性、保圆性(直线可以看成半径为无穷大的圆)和保对 称性,是一种重要的映射关系。 场论与复变函数Field Theory and Complex Variable Functions 20
场论与复变函数 Field Theory and Complex Variable Functions 20 第六章 共形映射 Conformal mapping 第二节 分式线性映射 分式线性映射 是一种常用的映 射,它可以看成由3种基本映射符合而成,在映射过程中具有 保角性、保圆性(直线可以看成半径为无穷大的圆)和保对 称性,是一种重要的映射关系。 az b w cz d

第六章共形映射 历零毛子代找大学 XIDIAN UNIVERSITY Conformal mapping 1.定义 形式为 az +b (ad-bc≠0) (6.2.1) cz +d 的映射称为分式线性映射。 对其求导: dw ad -bc dz (cz d)2 可以看出,当ad-bc≠0时,导数不为0,是共形映射. 并且,求反函数: -dw +b 2 cw -a ,(-a)(-d)-bc≠0 可以看出:分式线性映射的逆映射也是一个分式线性映射。 场论与复变函数Field Theory and Complex Variable Functions 21
场论与复变函数 Field Theory and Complex Variable Functions 21 第六章 共形映射 Conformal mapping 可以看出:分式线性映射的逆映射也是一个分式线性映射。 1.定义 形式为 的映射称为分式线性映射。 对其求导: 可以看出,当 时,导数不为0,是共形映射. 并且,求反函数: 0 az b w ad bc cz d - (6.2.1)