
第五章留数 历些毛子种技大学 XIDIAN UNIVERSITY Residues 5.1孤立奇点 1.定义 四2.分类 0 3.性质 m4.零点与极点的关系 场论与复变函数Field Theory and Complex Variable Functions
场论与复变函数 Field Theory and Complex Variable Functions 2 2 第五章 留数 Residues 1. 定义 2. 分类 3. 性质 4. 零点与极点的关系 5.1 孤立奇点

第五章留数 历安毛子代枚大学 XIDIAN UNIVERSITY Residues 定义 定义若f(z)在z处不解析,但在z的某个去心邻域 0<z-zo<内解析,则称为f(z)的孤立奇点 例如f(z)=e-z=0为孤立奇点 1 f(z)= z-1 2=1为孤立奇点 f(z)= 1 sin --z=0及z=11nπ(n=±1,±2,…)都是它的奇点 场论与复变函数Field Theory and Complex Variable Functions
场论与复变函数 Field Theory and Complex Variable Functions 3 3 第五章 留数 Residues 1. 定义 例如 z f z e 1 ( ) ----z=0为孤立奇点 z f z 1 sin 1 ( ) ----z=0及z=1/n (n = 1 , 2 ,…)都是它的奇点 1 1 ( ) z f z ----z=1为孤立奇点 定义 0 , ( ) . ( ) , 0 0 0 0 内解析 则 称 为 的孤立奇点 若 在 处不解析但 在 的某个去心邻域 z z z f z f z z z ~~~~~~~~~
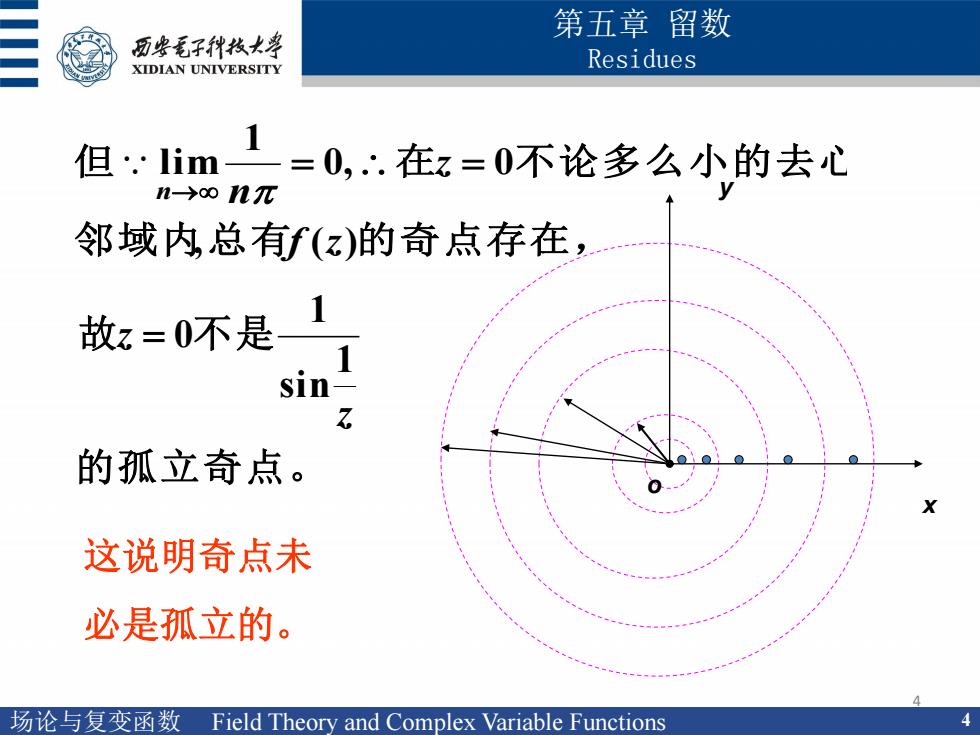
第五章留数 历安毛子代枚大等 XIDIAN UNIVERSITY Residues 但1im1=0,在z=0不论多么小的去心 n-→on元 邻域内总有f(z)的奇点存在, 故z=0不是1 sin- 的孤立奇点。 这说明奇点未 必是孤立的。 场论与复变函数Field Theory and Complex Variable Functions
场论与复变函数 Field Theory and Complex Variable Functions 4 4 第五章 留数 Residues x y o 这说明奇点未 必是孤立的。 邻域内总 有 的奇点存在, 但 在 不论多么小的去心 , ( ) 0, 0 1 lim f z z n n 的孤立奇点。 故 不 是 z z 1 sin 1 0

第五章留数 历些毛子代拔大学 XIDIAN UNIVERSITY Residues 2.分类 以下将f(z)在孤立奇点的邻域内展成洛朗级数,根 据展开式的不同情况,将孤立点进行分类。考察: =1-之+ sinz 352-+(-1) (2n+1)g 特点:没有负幂次项 2g=1-=+1+ n z 2! n! 特点:只有有限多个负幂次项 3e2=1+21+z2++ 21 特点:有无穷多个负幂次项 场论与复变函数Field Theory and Complex Variable Functions
场论与复变函数 Field Theory and Complex Variable Functions 5 5 第五章 留数 Residues 2. 分类 以下将f (z)在孤立奇点的邻域内展成洛朗级数,根 据展开式的不同情况,将孤立点进行分类。考察: (2 1)! ( 1) 3! 5! 1 sin (1) 2 4 2 n z z z z z n n 特点:没有负幂次项 2! ! 1 1 ! ! 1 (2) 1 0 1 0 n z z n z z n z z z e n n n n z n 特点:只有有限多个负幂次项 z n n e z z z ! 1 2! 1 (3) 1 1 2 1 特点:有无穷多个负幂次项

第五章留数 历些毛子代找大学 XIDIAN UNIVERSITY Residues 定义 设zo是f(2)的一个孤立奇点,在z的去心邻域内 若f(z)的洛朗级数 p ()f(z)=∑cn(z-z)” =0 没有负幂次项,称z=Z为可去奇点; (ii)f(z)=∑c(z-Z)(cm≠0,m≥1) 只有有限多个负幂次项,称z=z为m级极点; (imfz)=∑c,k-zo)” 1=-oo 有无穷多个负幂次项,称z=2为本性奇点。 场论与复变函数Field Theory and Complex Variable Functions
场论与复变函数 Field Theory and Complex Variable Functions 6 6 第五章 留数 Residues 定义 设z0是f (z)的一个孤立奇点,在z0 的去心邻域内 ,若f (z)的洛朗级数 0 0 ( ) ( ) ( ) n n n i f z c z z 没有负幂次项,称z=z0为可去奇点; ( ) ( ) ( 0 )( 0, 1) ii f z c z z c m m n m n n 只有有限多个负幂次项,称z=z0为m 级极点; n n n (iii) f (z) c (z z ) 0 有无穷多个负幂次项,称z=z0为本性奇点。 ~~~~~~~~ ~~~~~~~~ ~~~~~~~~