
第六章共形映射 历安毛子代枚大学 XIDIAN UNIVERSITY Conformal mapping 根据切向量的定义,可得: 1)Argz'(to)就是zo处C的切线正向与x轴正向间的夹角; 2) 相交于一点的两条曲线C与C2正向之间的夹角,就是它 们交点处两条切线正向间的夹角。 场论与复变函数Field Theory and Complex Variable Functions
场论与复变函数 Field Theory and Complex Variable Functions 7 第六章 共形映射 Conformal mapping 根据切向量的定义,可得: 1) Arg z '(t0 )就是z0处C的切线正向与x轴正向间的夹角; 2) 相交于一点的两条曲线C1与C2正向之间的夹角,就是它 们交点处两条切线正向间的夹角

第六章共形映射 历些毛子代枝大学 XIDIAN UNIVERSITY Conformal mapping 2.解析函数导数的几何意义 设函数w=fz)在区域D内解析,Z为D内的一点,且f(zo≠0.又设 C为z平面内通过点z的一条有向光滑曲线,其参数方程是: z=z(t),0≤t≤B, 它的正向相应于参数t增大的方向,且zo=z(to,z'(to≠0,toB, 则映射w=fz)将C映射成w平面内通过点w。fzo)的一条有向光 滑曲线)其参数方程是 w=f几z(t)],ost≤B 正向相应于参数t增大的方向. 场论与复变函数Field Theory and Complex Variable Functions 8
场论与复变函数 Field Theory and Complex Variable Functions 8 第六章 共形映射 Conformal mapping 2.解析函数导数的几何意义 设函数w=f(z)在区域D内解析, z0为D内的一点, 且f ‘(z0 )0. 又设 C为z平面内通过点z0的一条有向光滑曲线, 其参数方程是: z=z(t), atb, 它的正向相应于参数t增大的方向, 且z0=z(t0 ), z ’(t0 )0, a<t0<b. 则映射w=f(z)将C映射成w平面内通过点w0=f(z0 )的一条有向光 滑曲线G, 其参数方程是 w=f[z(t)], atb 正向相应于参数t增大的方向
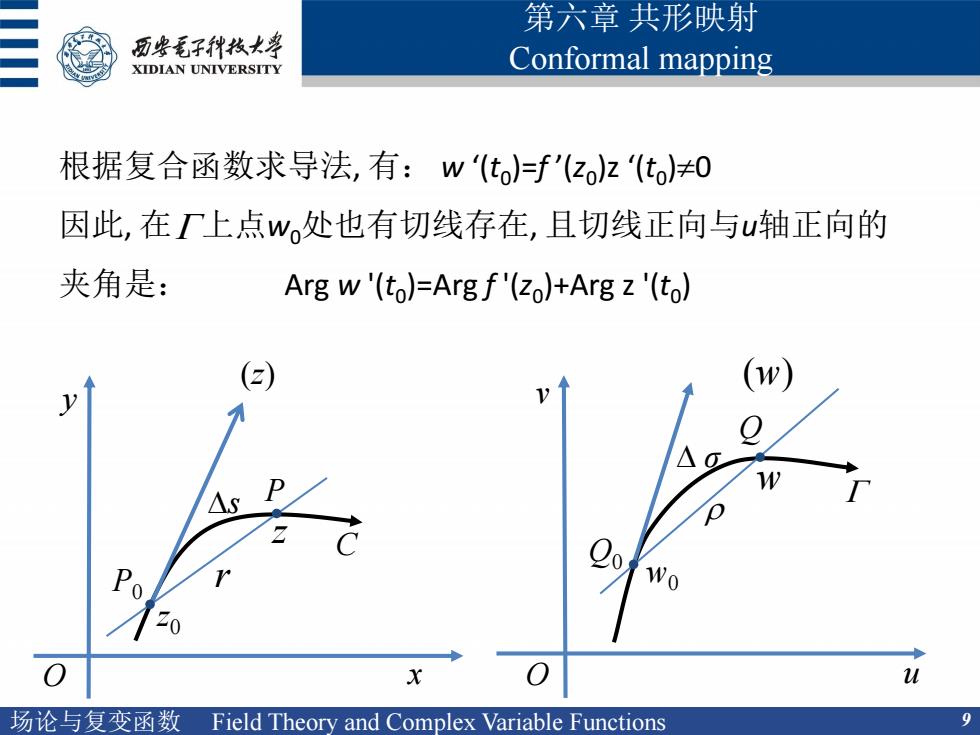
第六章共形映射 历安毛子代枚大等 XIDIAN UNIVERSITY Conformal mapping 根据复合函数求导法,有:w'(to)=f'(zoz《to≠0 因此,在T上点w处也有切线存在,且切线正向与u轴正向的 夹角是: Arg w'(to)=Arg f'(zo)+Arg z '(to) (z) y D u 场论与复变函数Field Theory and Complex Variable Functions
场论与复变函数 Field Theory and Complex Variable Functions 9 第六章 共形映射 Conformal mapping 根据复合函数求导法, 有: w ‘(t0 )=f ’(z0 )z ‘(t0 )0 因此, 在 上点w0处也有切线存在, 且切线正向与u轴正向的 夹角是: Arg w '(t0 )=Arg f '(z0 )+Arg z '(t0 ) x z0 P0 r z P Ds C (z) O G O u G w0 Q0 Q w r D σ (w) y v

第六章共形映射 历些毛子代找大学 XIDIAN UNIVERSITY Conformal mapping 或者有 Arg f'(Zo)=Arg w'(to)-Arg z'(to) (6.1.1) 如果将z点处的切线正向与w点处的切线正向之间的夹角理解 为曲线c经过w=f孔z)映射后在z处的转动角,则(6.1.1)式表明: 1)导数f'zo≠0的辐角Arg f '(z是曲线C经过w=fz映射后在z处 的转动角; 2)转动角的大小与方向跟曲线C的形状与方向无关,所以这种 映射具有转动角的不变性, 场论与复变函数Field Theory and Complex Variable Functions 10
场论与复变函数 Field Theory and Complex Variable Functions 10 第六章 共形映射 Conformal mapping 或者有 Arg f ‘(z0 ) =Arg w ’(t0 )-Arg z ‘(t0 ) (6.1.1) 如果将z0点处的切线正向与w0点处的切线正向之间的夹角理解 为曲线C经过w=f(z)映射后在z0处的转动角, 则(6.1.1)式表明: 1)导数f ’(z0 )0的辐角Arg f ‘(z0 )是曲线C经过w=f(z)映射后在z0处 的转动角; 2)转动角的大小与方向跟曲线C的形状与方向无关,所以这种 映射具有转动角的不变性
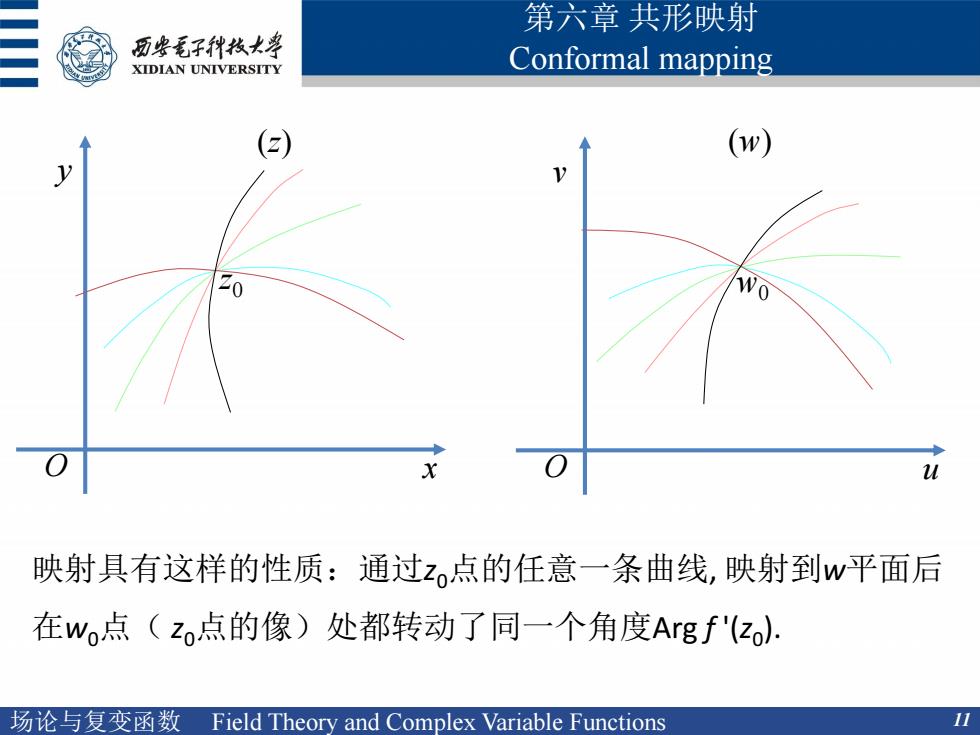
第六章共形映射 历安毛子代枚大学 XIDIAN UNIVERSITY Conformal mapping (w) y 映射具有这样的性质:通过z点的任意一条曲线,映射到w平面后 在w点(zo点的像)处都转动了同一个角度Argf'(zo). 场论与复变函数Field Theory and Complex Variable Functions 11
场论与复变函数 Field Theory and Complex Variable Functions 11 第六章 共形映射 Conformal mapping 映射具有这样的性质:通过z0点的任意一条曲线, 映射到w平面后 在w0点( z0点的像)处都转动了同一个角度Arg f '(z0 ). O x y O u v (z) (w) z0 w0