中国科学技术大学：《计算机视觉》课程教学资源（PPT课件讲稿）第七章 基于运动视觉的场景复原 Shape（Structure）From Motion

基于外极线的三维运动估计 基本矩阵的性质 detE=0 ET=([TR)T=RTT --RTXT-0 ET=0 EET=([TIR)(T]R)=([TI RR)IT]-(TT)I-TT EET =(TT)I-TTT 外极线方程的待求参数 5个未知的独立的参数，这也和运动参数的自由度 数量相一致，即三个旋转自由度，二个平移自由度 或三个关于一个比例系数的平移自由度)·

基于外极线的三维运动估计  基本矩阵的性质    外极线方程的待求参数 5个未知的独立的参数，这也和运动参数的自由度 数量相一致，即三个旋转自由度，二个平移自由度 （或三个关于一个比例系数的平移自由度）. detE = 0 E T = 0 T T T EE T T I TT T = ( ) − E T = ([T] R) T = R [T] T = −R TT = 0 T T x T T x T T T T x T x T EE T xR T xR T RR T T T I TT T = ([ ] )([ ] ) = ([ ] )[ ] = ( ) −

(1)根据基本矩阵估计运动 1.计算基本矩阵 eoo eol e02 E= eoo e10 e11 e12 e20 e21 e22 XkIXk XktIyk x+1 +xy+yy+1x发) 0 2 a/x-0 4X=0 e21 8对以上对应点求稳定解（实际经常使用 RANSAC算法)

(1) 根据基本矩阵估计运动 1. 计算基本矩阵           = 20 21 22 10 11 12 00 01 02 e e e e e e e e e E ( 1) 0 2 2 2 1 2 0 1 2 1 1 1 0 0 2 0 1 0 0 1 1 1 1 1 1 =                                           + + + + + + e e e e e e e e e x x x y x y x y y y x y k k k k k k k k k k k k a X = 0 T k 0 , X = T An k 8对以上对应点求稳定解(实际经常使用 RANSAC算法)

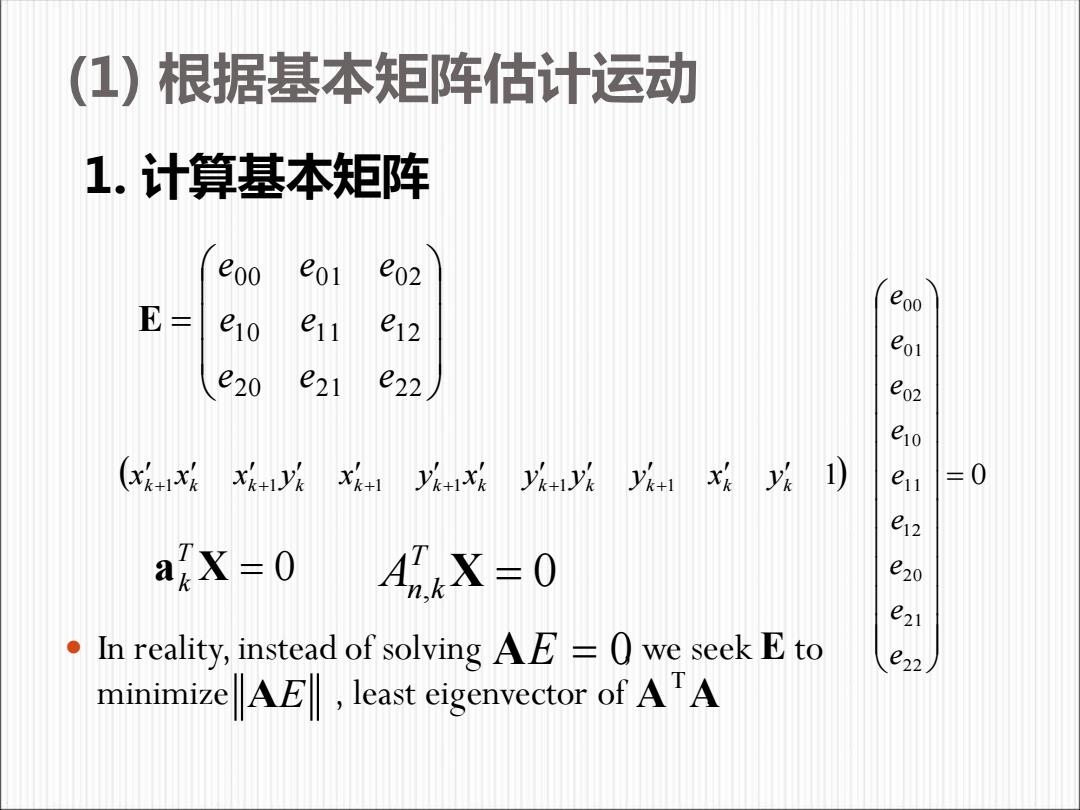
(1)根据基本矩阵估计运动 1.计算基本矩阵 eoo eol e02 E= eoo e10 e11 e12 e20 e21 e22 (XkXk Xkyk Xk+ yyy yxy 1) aX-0 A死X=0 21 In reality,instead of solving AE=0 we seek E to e22 minimizeAF,least eigenvector of AA

(1) 根据基本矩阵估计运动 1. 计算基本矩阵           = 20 21 22 10 11 12 00 01 02 e e e e e e e e e E ( 1) 0 2 2 2 1 2 0 1 2 1 1 1 0 0 2 0 1 0 0 1 1 1 1 1 1 =                                           + + + + + + e e e e e e e e e x x x y x y x y y y x y k k k k k k k k k k k k a X = 0 T k 0 , X = T An k  In reality, instead of solving , we seek E to minimize , least eigenvector of . AE = 0 AE A A 

8-point algorithm To enforce that E is of rank 2,E is replaced by E'that minimizes subject to IE-E‖ det E'-0 It is achieved by SVD.Let E=UV,where ∑ let then E'-UZ'VTis the solution

8-point algorithm  To enforce that E is of rank 2, E is replaced by E’ that minimizes subject to . E E − ' det ' 0 E = • It is achieved by SVD. Let , where , let then is the solution. E Σ  = U V           = 3 2 1 0 0 0 0 0 0 Σ              = 0 0 0 0 0 0 0 Σ' 2 1   E ' Σ'  = U V

8-point algorithm Build the constraint matrix A=[x2(1,).*x1(1,)x2(1,).*x1(2,)x2(1,)'… x2(2,.*x1(1,)x2(2,)八*x1(2,:)x2(2, x1(1,: x1(2,)' ones(npts,1)]; [U,D,V]=svd(A); Extract fundamental matrix from the column ofV corresponding to the smallest singular value. E=reshape(V(:,9),3,3)'; Enforce rank2 constraint [U,D,V]=svd(E); E=U*diag([D(1,1)D(2,2)0])*V';

8-point algorithm % Build the constraint matrix A = [x2(1,:)‘.*x1(1,:)' x2(1,:)'.*x1(2,:)' x2(1,:)' ... x2(2,:)'.*x1(1,:)' x2(2,:)'.*x1(2,:)' x2(2,:)' ... x1(1,:)' x1(2,:)' ones(npts,1) ]; [U,D,V] = svd(A); % Extract fundamental matrix from the column of V % corresponding to the smallest singular value. E = reshape(V(:,9),3,3)'; % Enforce rank2 constraint [U,D,V] = svd(E); E = U*diag([D(1,1) D(2,2) 0])*V';