中国科学技术大学：《计算机视觉》课程教学资源（PPT课件讲稿）第七章 基于运动视觉的场景复原 Shape（Structure）From Motion

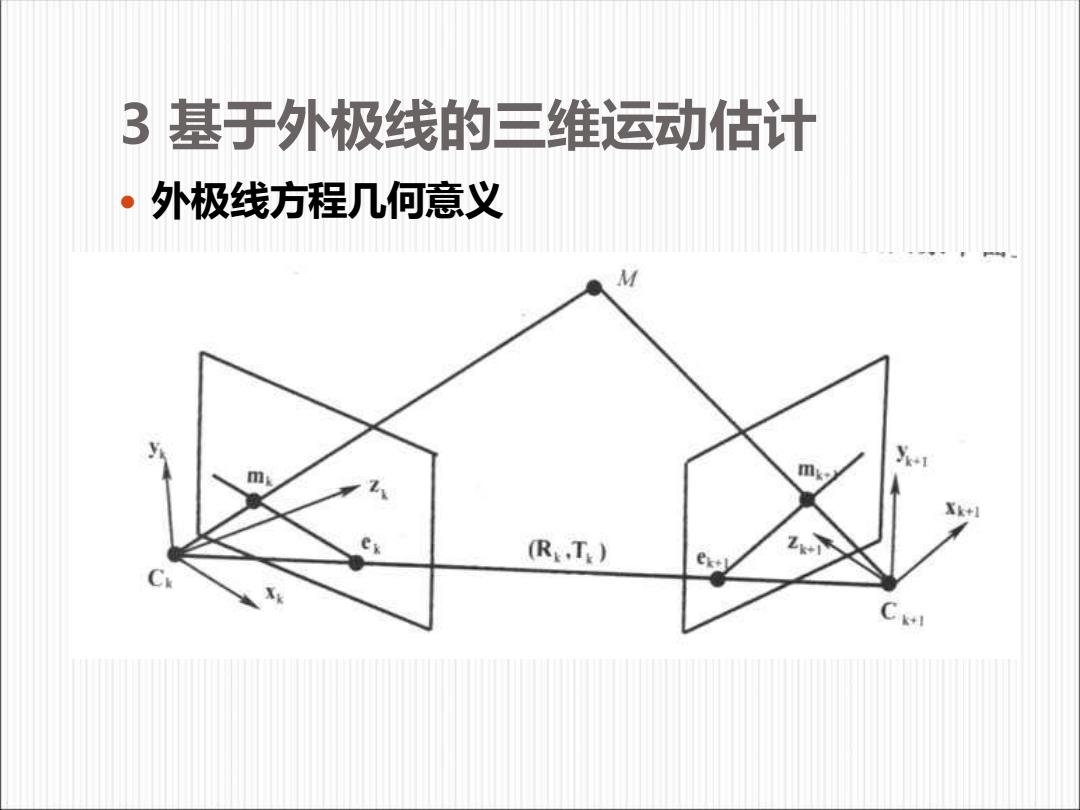
3基于外极线的三维运动估计 。 外极线方程几何意义 m (R:.T.) C

3 基于外极线的三维运动估计  外极线方程几何意义

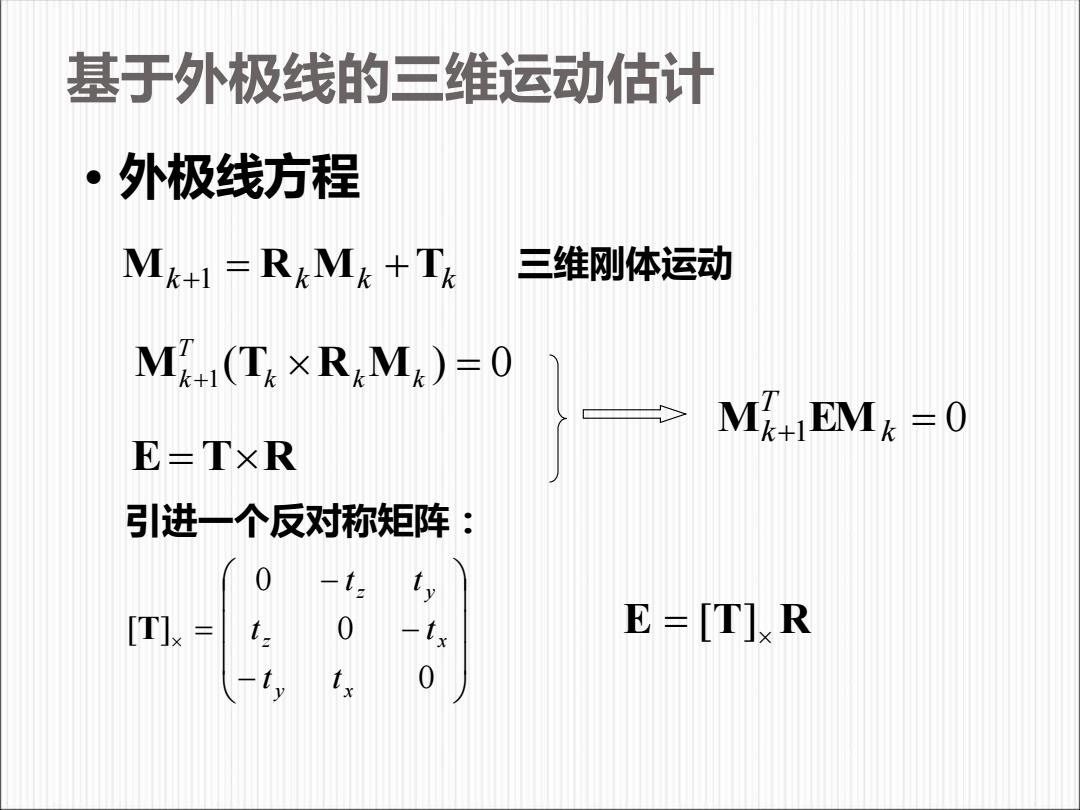
基于外极线的三维运动估计 外极线方程 Mk+1 =RkMk+Tk 三维刚体运动 M1(Tk×RkM6)=0 MEM=0 E-TxR 引进一个反对称矩阵： [T]k= E=[TIR

基于外极线的三维运动估计 • 外极线方程 Mk+1 = Rk Mk +Tk 三维刚体运动 1 ( ) 0 T M T R M k k k k +  = E=TR +1 k = 0 T Mk EM           − − −  = 0 0 0 [ ] y x z x z y t t t t t t T E = [T]  R 引进一个反对称矩阵：

基于外极线的三维运动估计 基本矩阵(essential matrix) E=T×R E=[T]×R [TI= 平移矢量乘以不为零的系数，不影响外极线方程 成立 所恢复的运动参数是关于比例系数的解

基于外极线的三维运动估计 • 基本矩阵（essential matrix） E=TR E = [T]  R             − − −  = 0 0 0 [ ] y x z x z y t t t t t t T 平移矢量乘以不为零的系数，不影响外极线方程 成立 所恢复的运动参数是关于比例系数的解

本质矩阵的应用 可被用于 -简化匹配问题 检测错误的匹配

本质矩阵的应用 • 可被用于 – 简化匹配问题 – 检测错误的匹配

基于外极线的三维运动估计 外极线方程 Zk-k+1 MEM=0 Xk+1 yk+1 1)E =0 Zk+1 2k+1 x=FX y 1 mK+1Emk=0— (Xk+1 Yk+1 1)E =0 1

基于外极线的三维运动估计 • 外极线方程 +1 k = 0 T Mk EM 0 1 ( 1) 1 1 1 1 =                   + + + + k k k k k k k k z y z x z y z x E 0 1 ( 1) 1 1 =               + + k k k k y x ~ ~ 0 x y E +1 k = T mk Em z y y  = F z x x  = F k k+1 z z