北京航空航天大学：《数字图像处理》课程教学资源（PPT课件）第十一章 图象重建

物理上X射线到人体有个衰减过程： Ng=N exp∫4(x,yds u(x,y)为x,y点的衰减 Nn:入射X射线（光子)强度 N。：射线穿透物体后被检测到的射线强度 u(x,y):反映了人体各部组织的性质，在空间上的分布就形成了人体 各部组织的图象，所以u(x,y)实质上反映了图象灰度分布f(x,y) 得：n"=h ※上述为一个切面，一系列切面构成三维物体，两种方法：直 接、间接。 教字图像处要 ■■■

物理上X射线到人体有个衰减过程： u(x,y)为x,y点的衰减 Nin ：入射X射线（光子）强度 Nd ：X射线穿透物体后被检测到的射线强度 u(x,y)：反映了人体各部组织的性质，在空间上的分布就形成了人体 各部组织的图象，所以u(x,y)实质上反映了图象灰度分布f(x,y)  ( )   = − 射 N N u x y ds d in exp , ( )   =      射 得： u x y ds N N d in ln , ※上述为一个切面，一系列切面构成三维物体，两种方法：直 接、间接

9.2基本原理： 对图像函数f(x,y)付氏变换： F(u,y)=广心fx,y)exp[-j2zlc+ykd Pt)的付氏变换 So(w)=po(t)exp[-j2nwildt 当0=0时，t=x,S=y,w=u S(d)=p(x)exp[-j2πx] 教字图像处姿 ■■■■

( ) ( )  ( )    −  − F u,v = f x, y exp − j2 ux + v y dxdy 9.2 基本原理： 对图像函数f(x,y)付氏变换: ( ) ( ) ( )   t x s y w u S w p t j wt dt P t = = = = = −  − 0 , , , exp 2 当 时 的付氏变换      S (u) p (x)exp j2uxdx 0 = 0 −  −

当v=0时， Fu,0)=j∫flx,y吵expl-j2m小dkd -exp2 故有：F(u,0)=Jp,(expl-j2mk=S,卿S,6w】 教字图像处要 ■■

当 v=0 时， ( ) ( )   f (x y)dy  j uxdx F u f x y j ux dxdy   , exp 2 ,0 , exp 2  −     = =  −     −  −  − ( ) ( )   ( ) ( )   − 故有：F u,0 = p0 x  exp − j2ux dx = S0 u 即S0 w

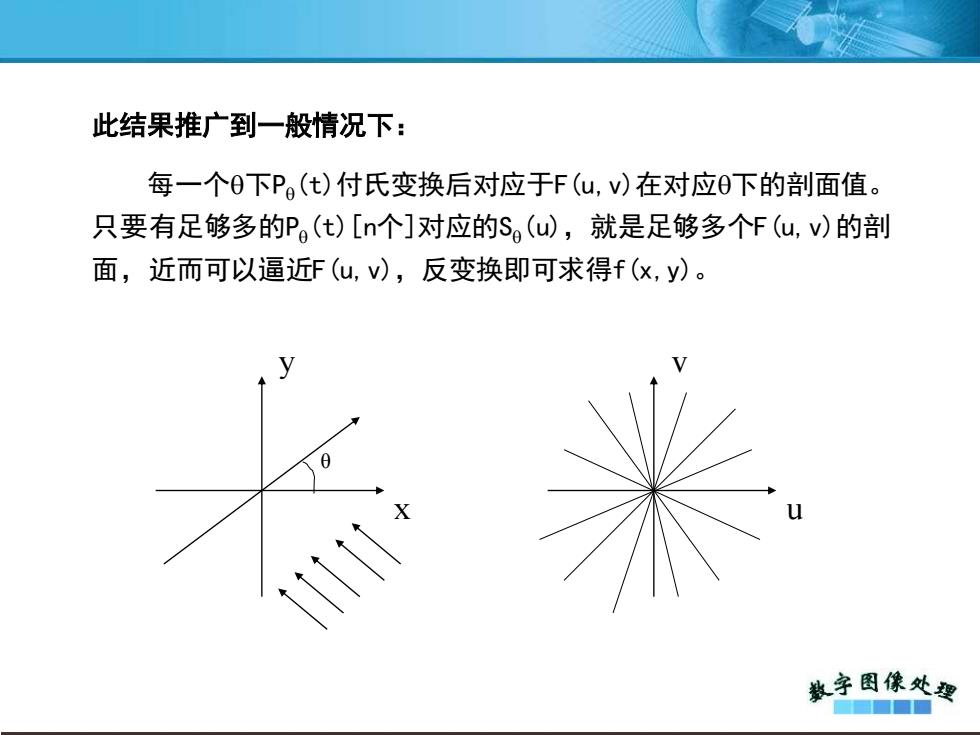
此结果推广到一般情况下： 每一个0下P(t)付氏变换后对应于F(u,v)在对应0下的剖面值。 只要有足够多的P(t)[n个]对应的S(u),就是足够多个F(u,v)的剖 面，近而可以逼近F(u,v),反变换即可求得f(x,y)。 教字图像处要 ■■■■

此结果推广到一般情况下： 每一个下P(t)付氏变换后对应于F(u,v)在对应下的剖面值。 只要有足够多的P (t)[n个]对应的S (u)，就是足够多个F(u,v)的剖 面，近而可以逼近F(u,v)，反变换即可求得f(x,y)。 x y θ u v

由付氏变换旋转不变性： 得：Sa(w)=F(w,θ)=F(u,) (一般的S(w)=F(u,v)的证明) 证：f(t,s)是f(x,y)在t,s坐标上为函数 日-lea。ao Po()=[f(t.s).ds S(w)=[po()edi=fs)dsedt 这里/=rcs0+)如6 s=-xsin+ycos0 代入由1,5→x,y习 教字图像处要

由付氏变换旋转不变性： 得： S  (w) = F(w, ) = F(u,v) （一般的S (w)=F(u,v)的证明） 证：f(t,s)是f(x,y)在t,s坐标上为函数 ( ) ( )  − =             − =      p t f t s ds y x s t , sin cos cos sin      x t y s θ u ω v θ ( ) ( ) ( )      = − + → = + =  =    −  − −  −   s x y t s x y t x y S w p t e dt f t s ds e dt j wt j wt sin cos , , cos sin , 2 2 代入由 这里        