
第二章电感电容压控振荡器 (a)理想电感电容并联电路 (b)实际电感电容并联电路 (c)RLC并联等效电路 图2.3电感电容谐振回路 180 (2.5) 实际上,随着振荡幅度的增大,每一级将进入非线性甚至出现振幅受到限制的“饱和”现象。 因此在大信号振荡情况下,环形振荡器中倒相器的直流增益往往比式子(2.5)要大2-3倍。这 样才能保证环形振荡器在大信号,非线性振荡情况下,其平均环路增益能够始终为1。 两端负反馈系统分析方法对于环形振荡器的分析是非常有效的,然而电感电容振荡器电 路很难简单地看作等效成一个负反馈系统。因此我们必须采用下述的单端能量补偿系统分析 方法。 2.1.2单端能量补偿系统分析 对于一个理想的电感电容谐振电路(图2.3(a),在频率om=1√LC处,电感的感抗lom 与电容的容抗/jC®大小相等,符号相反。这时电感电容回路开始振荡,回路的品质因数 Q为无穷大。根据后面第三章和第四章的分析,实际的片上电感和电容都存在串联电阻。如 图23(b)所示,R和Rc分别是电感和电容的串联电阻。根据电感和电容的串联一并联转换 关系,图2.3(b)可以由图2.3(c)中的RLC并联等效电路来代替,其中并联电感Lp,电阻Rp 和电容C分别为, C +o Cp=- Rr=RrL+Rrc =(1+Qi)R.+(1+Q)Rc (2.6 1+ Q3 其中,电感支路品质因数2,=,电容支路品质因数Q。=,RLC并联谐振回路的品 R OCR 质因数Qmt= =C,R,谐振频率@。=W,C,。在谐振须率处,RLC并联等效电路的 OL 输出阻抗为Rp。 如图2.4(a)所示,当有一个电流脉冲刺激RLC并联电路时,RLC电路将发生振荡,由于 电阻Rp的存在,振荡将慢慢衰减为零。如果将一个“负阻Rp”与RLC电路相并联,如图 2.4b),RLC电路的并联电阻为0,这样振荡将永远维持下去。然而实际电路中,不存在一 个理想的“负阻”,“负阻”都是由有源器件等效而来。图2.4可以看出振荡器电路能够一直 保持振荡,其能量是来源于电路中的有源器件的供给。因此对于一个振荡器电路,我们可以 将电路划分为两个部分:正阻电路(耗能部分)和负阻电路(提供能量部分)。图2.4(c)的左边是 一个谐振回路,产生振荡频率。:右边是一个提供能量的负阻电路。我们将上述分析振荡 电感电容压控振荡器 9
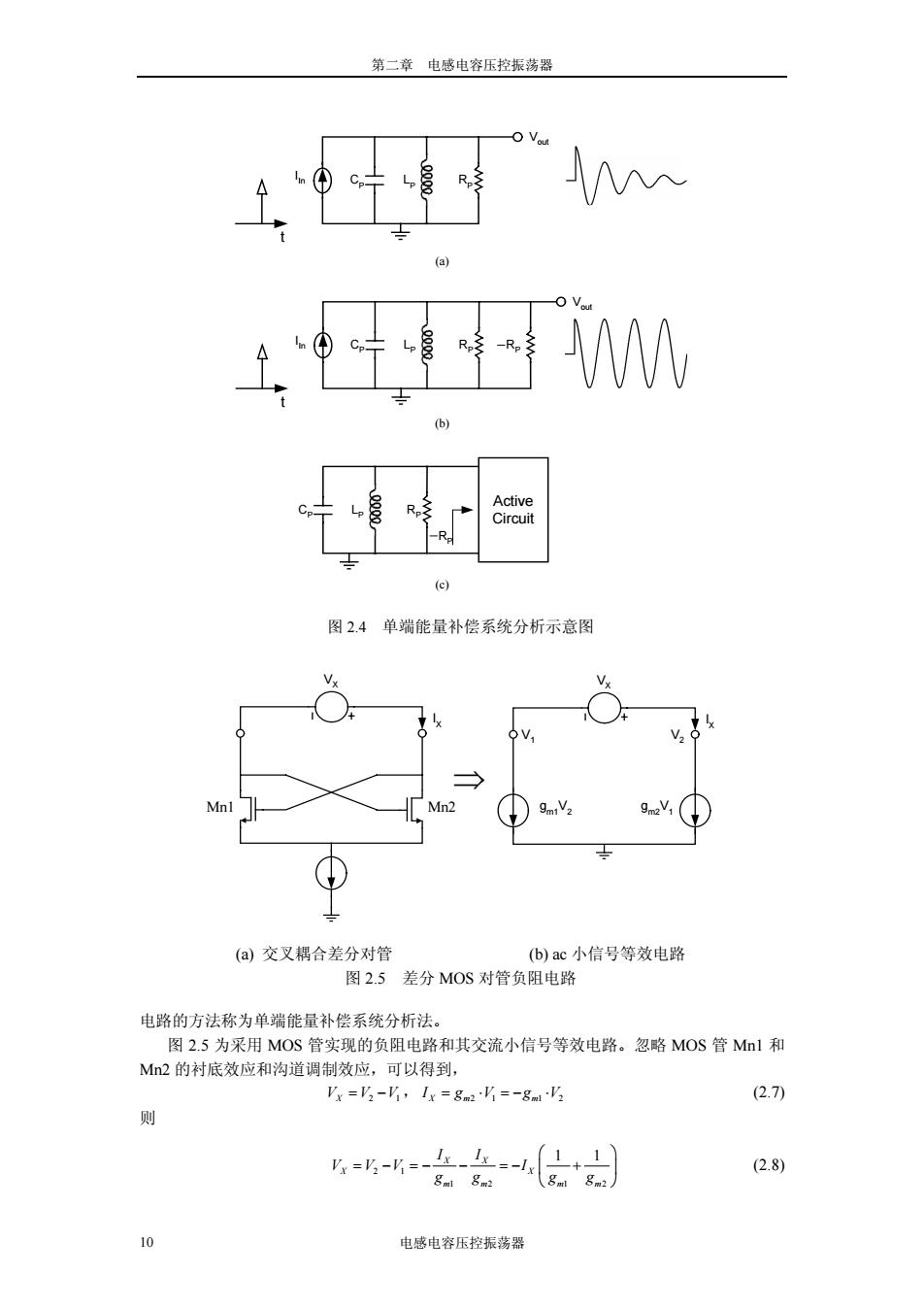
第二章 电感电容压控振荡器 电感电容压控振荡器 9 2 0 180 A 1 tan N ° ⎛ ⎞ ⎛ ⎞ = + ⎜ ⎟ ⎜ ⎟ ⎝ ⎠ ⎝ ⎠ (2.5) 实际上,随着振荡幅度的增大,每一级将进入非线性甚至出现振幅受到限制的“饱和”现象。 因此在大信号振荡情况下,环形振荡器中倒相器的直流增益往往比式子(2.5)要大 2-3 倍。这 样才能保证环形振荡器在大信号,非线性振荡情况下,其平均环路增益能够始终为 1。 两端负反馈系统分析方法对于环形振荡器的分析是非常有效的,然而电感电容振荡器电 路很难简单地看作等效成一个负反馈系统。因此我们必须采用下述的单端能量补偿系统分析 方法。 2.1.2 单端能量补偿系统分析 对于一个理想的电感电容谐振电路(图 2.3(a)),在频率 1 ωres = LC 处,电感的感抗 res jLω 与电容的容抗1 res jCω 大小相等,符号相反。这时电感电容回路开始振荡,回路的品质因数 Q 为无穷大。根据后面第三章和第四章的分析,实际的片上电感和电容都存在串联电阻。如 图 2.3(b)所示,RL和 RC分别是电感和电容的串联电阻。根据电感和电容的串联-并联转换 关系,图 2.3(b)可以由图 2.3(c)中的 RLC 并联等效电路来代替,其中并联电感 LP,电阻 RP 和电容 CP分别为, 2 1 1 P L L L Q ⎛ ⎞ = + ⎜ ⎟ ⎝ ⎠ , 2 1 1 P C C C Q = + , ( ) ( ) 2 2 , , 1 1 R R R QR QR P = + =+ ++ PL PC L L C C (2.6) 其中,电感支路品质因数 L L L Q R ω = ,电容支路品质因数 1 C C Q ωCR = ,RLC 并联谐振回路的品 质因数 P tank p p P R Q CR L ω ω = = ,谐振频率 1 ωres P P = L C 。在谐振频率处,RLC 并联等效电路的 输出阻抗为 RP。 如图 2.4(a)所示,当有一个电流脉冲刺激 RLC 并联电路时,RLC 电路将发生振荡,由于 电阻 RP 的存在,振荡将慢慢衰减为零。如果将一个“负阻-RP”与 RLC 电路相并联,如图 2.4(b),RLC 电路的并联电阻为 0,这样振荡将永远维持下去。然而实际电路中,不存在一 个理想的“负阻”,“负阻”都是由有源器件等效而来。图 2.4 可以看出振荡器电路能够一直 保持振荡,其能量是来源于电路中的有源器件的供给。因此对于一个振荡器电路,我们可以 将电路划分为两个部分:正阻电路(耗能部分)和负阻电路(提供能量部分)。图 2.4(c)的左边是 一个谐振回路,产生振荡频率ω0 ;右边是一个提供能量的负阻电路。我们将上述分析振荡 L C L C RL RC RP LP (a) 理想电感电容并联电路 (b) 实际电感电容并联电路 (c) RLC 并联等效电路 图 2.3 电感电容谐振回路
第二章电感电容压控振荡器 ●)V R (b) R Active Circuit (c) 图2.4单端能量补偿系统分析示意图 Mnl Mn2 9mV1 (a)交叉耦合差分对管 (b)ac小信号等效电路 图2.5差分MOS对管负阻电路 电路的方法称为单端能量补偿系统分析法。 图2.5为采用MOS管实现的负阻电路和其交流小信号等效电路。忽略MOS管Mn1和 M2的衬底效应和沟道调制效应,可以得到, 'x='3-,Ix=gm2=-gm1'2 (2.7) 则 女女 (2.8) O 电感电容压控振荡器
第二章 电感电容压控振荡器 10 电感电容压控振荡器 电路的方法称为单端能量补偿系统分析法。 图 2.5 为采用 MOS 管实现的负阻电路和其交流小信号等效电路。忽略 MOS 管 Mn1 和 Mn2 的衬底效应和沟道调制效应,可以得到, V VV X = −2 1, Xm m 21 12 I = gV gV ⋅ =− ⋅ (2.7) 则 2 1 12 12 X X 1 1 X X mm mm I I V VV I gg gg ⎛ ⎞ = − =− − =− + ⎜ ⎟ ⎝ ⎠ (2.8) I In CP RP LP t Vout I In CP RP LP t Vout RP CP RP LP Active Circuit RP (a) (b) (c) 图 2.4 单端能量补偿系统分析示意图 Mn1 Mn2 VX I X VX I X V1 V2 gm2V1 gm1V2 ⇒ (a) 交叉耦合差分对管 (b) ac 小信号等效电路 图 2.5 差分 MOS 对管负阻电路
第二章电感电容压控振荡器 Ce Lp 000'0 X 2 8 Mnl Mn2 图2.6负跨导交叉耦合电感电容振荡器等效电路 一8m A CCO R B GIC (a) (b) (c) 图2.7单MOS管负阻电路 如果Mnl管和Mn2管相同,即gm1=gm2=gm,得 =2 (2.9) Ix 8m 当加在负阻的两端的电压增加时,负阻将对外输出电流。如果将图2.5()中的交叉耦合 差分对管与RLC回路相并联,并且保证R。≤2/gm时,负阻就能够为RLC回路中的并联电 阻Rp消耗的能量进行源源不断的补偿。图2.6为交叉耦合负跨导电感电容振荡器等效电路, 节点X和Y将产生差分振荡信号,振荡波形与尾电流偏置大小有关,具体分析将在第六章 中做详细论述。 另外一种产生负阻的方法如图2.7所示。忽略MOS管M1的衬底效应和沟道调制效应, 可以得到M的电流为1=8m(←1x/C,),电压Vx为 h=u-1)+-+8片+ C,s Cs Cs C2s Cs 1+1 (2.10) 电感电容压控振荡器 1
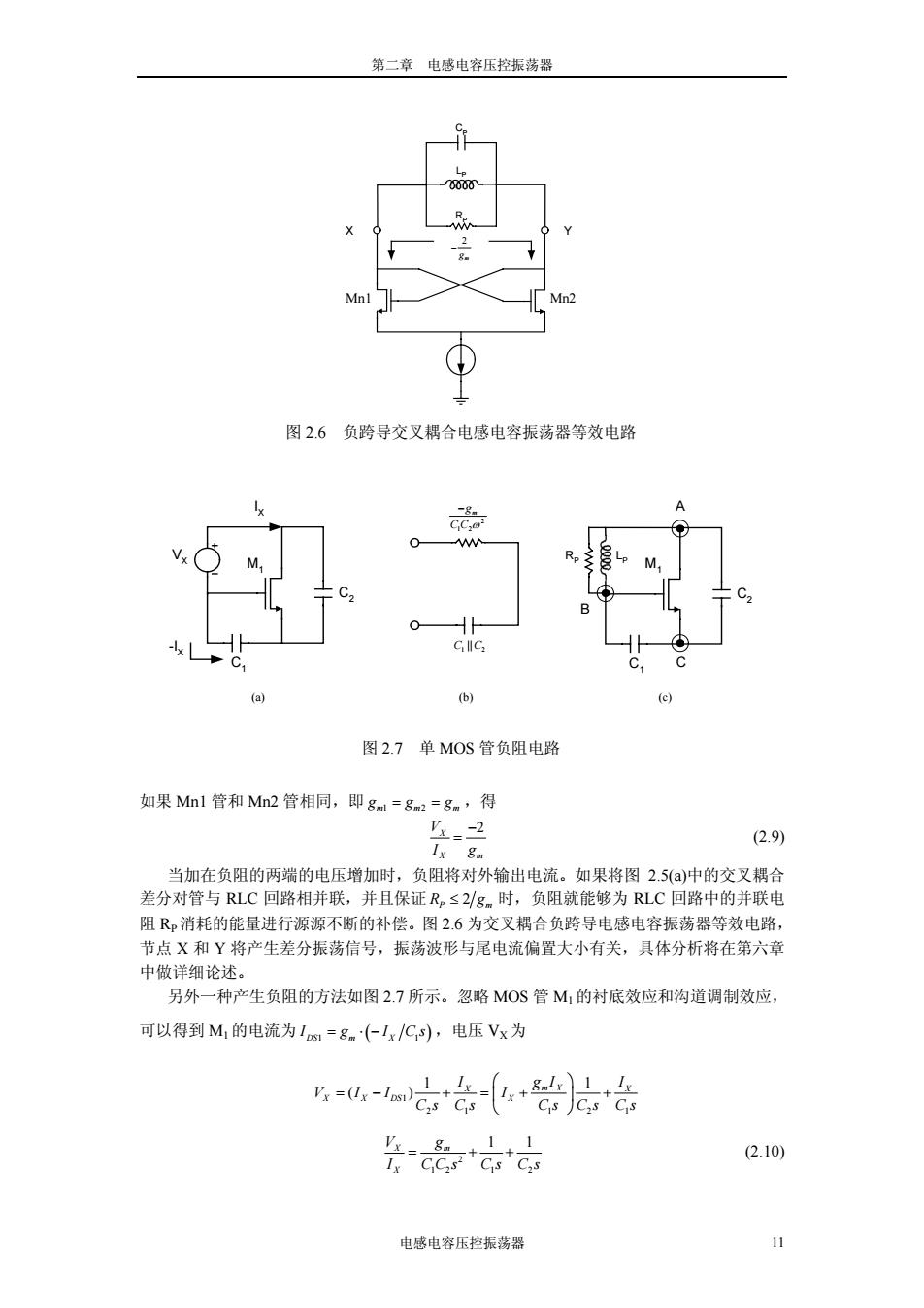
第二章 电感电容压控振荡器 电感电容压控振荡器 11 如果 Mn1 管和 Mn2 管相同,即 mm m 1 2 g = g g = ,得 X 2 X m V I g − = (2.9) 当加在负阻的两端的电压增加时,负阻将对外输出电流。如果将图 2.5(a)中的交叉耦合 差分对管与 RLC 回路相并联,并且保证 2 R g P ≤ m 时,负阻就能够为 RLC 回路中的并联电 阻 RP消耗的能量进行源源不断的补偿。图 2.6 为交叉耦合负跨导电感电容振荡器等效电路, 节点 X 和 Y 将产生差分振荡信号,振荡波形与尾电流偏置大小有关,具体分析将在第六章 中做详细论述。 另外一种产生负阻的方法如图 2.7 所示。忽略 MOS 管 M1 的衬底效应和沟道调制效应, 可以得到 M1 的电流为 IDS m X 1 1 = ⋅− g I Cs ( ) ,电压 VX为 1 21 1 21 1 1 ( ) X m X X X X DS X I g I I V II I Cs Cs Cs Cs Cs ⎛ ⎞ =− += + + ⎜ ⎟ ⎝ ⎠ 2 1 2 1 2 X m 1 1 X V g I CC s Cs Cs = ++ (2.10) Mn1 Mn2 CP RP LP 2 m g − X Y 图 2.6 负跨导交叉耦合电感电容振荡器等效电路 VX M1 C2 C1 I X -IX 2 1 2 m g C C ω − 1 2 C C|| M1 C2 C1 RP LP A B C (a) (b) (c) 图 2.7 单 MOS 管负阻电路

第二章电感电容压控振荡器 V。一0000 (b) (c) 图2.8不同结构的单管振荡器 从式子(2.10),可以知道图2.7(a)中的M1的栅漏之间的阻抗包括一个负阻-g/C,C,o2与电 容C1和C2的并联,其等效电路图如图2.7b)所示。当在M1的栅漏之间并联一个电感,如 图2.7(c),该电路将形成振荡器电路。将A,B和C三点分别接地的不同,可以构成三种不同 结构的振荡器。它们分别如图2.8(),(b)和(c)所示,图中的电流源I提供振荡器的直流偏置。 图2.8(a)是A点接地情况,它是一个源极跟随器结构:图2.8b)是B点接地情况,它是通常 使用比较广泛的考毕兹振荡器(Colpitts Oscillator)):图2.8(c)为C点接地,它是前面所述的负 跨导振荡器的单端形式。 对环形振荡器和电感电容振荡器的分析,我们知道两端负反馈系统分析方法广泛用于环 形振荡器电路的分析,而单端能量补偿系统分析方法在电感电容振荡器电路的分析中广泛被 采用。 2.2电感电容压控振荡器 上一节介绍的是振荡器振荡的基本机理,而且振荡器的谐振频率是一个固定值。为了使 得振荡器的谐振频率能够克服工艺和温度的偏差,以及满足特定应用场合中信道带宽的要 求,我们需要设计具有一定调谐范围的压控振荡器。因为环形振荡器电路不是本论文研究的 重点,在没有特定申明的情况下,后面章节中提到的振荡器都是指电感电容振荡器。 2.2.1压控振荡器的数学模型 一个理想的压控振荡器的频率压控特性(图2.9)可以表示为, 0oa=o6+Kr·'m (2.11) 其中V为压控电压,K,为压控振荡器的增益,O。为压控电压为OV时的振荡频率。 振荡器的频率与相位的关系表示为, (2.12) 则根据式子(2.11)和(2.12),假设K,为常数,可以得到振荡器的相位为, p=」omdi+4。=J(oo+Kr'ni)d+4。=oot+K,J',di+4 (2.13) 其中定义振荡器的相位增量为p=K,「V,dt。因此在锁相环电路中,压控振荡器是相位的 一个理想的积分器,其传递函数可以表示为, 色 (2.14) 电感电容压控振荡器
第二章 电感电容压控振荡器 12 电感电容压控振荡器 从式子(2.10),可以知道图 2.7(a)中的 M1 的栅漏之间的阻抗包括一个负阻 2 m 1 2 −g CC ω 与电 容 C1 和 C2 的并联,其等效电路图如图 2.7(b)所示。当在 M1 的栅漏之间并联一个电感,如 图 2.7(c),该电路将形成振荡器电路。将 A,B 和 C 三点分别接地的不同,可以构成三种不同 结构的振荡器。它们分别如图 2.8(a),(b)和(c)所示,图中的电流源 I1 提供振荡器的直流偏置。 图 2.8(a)是 A 点接地情况,它是一个源极跟随器结构;图 2.8(b)是 B 点接地情况,它是通常 使用比较广泛的考毕兹振荡器(Colpitts Oscillator);图 2.8(c)为 C 点接地,它是前面所述的负 跨导振荡器的单端形式。 对环形振荡器和电感电容振荡器的分析,我们知道两端负反馈系统分析方法广泛用于环 形振荡器电路的分析,而单端能量补偿系统分析方法在电感电容振荡器电路的分析中广泛被 采用。 2.2 电感电容压控振荡器 上一节介绍的是振荡器振荡的基本机理,而且振荡器的谐振频率是一个固定值。为了使 得振荡器的谐振频率能够克服工艺和温度的偏差,以及满足特定应用场合中信道带宽的要 求,我们需要设计具有一定调谐范围的压控振荡器。因为环形振荡器电路不是本论文研究的 重点,在没有特定申明的情况下,后面章节中提到的振荡器都是指电感电容振荡器。 2.2.1 压控振荡器的数学模型 一个理想的压控振荡器的频率压控特性(图 2.9)可以表示为, ωout V ctrl =+⋅ ω0 K V (2.11) 其中Vctrl 为压控电压, KV 为压控振荡器的增益,ω0 为压控电压为 0V 时的振荡频率。 振荡器的频率与相位的关系表示为, out d dt φ ω = (2.12) 则根据式子(2.11)和(2.12),假设 KV 为常数,可以得到振荡器的相位为, ( ) out V ctrl V ctrl 0 0 00 0 φ = ω φ ω φω φ dt K V dt t K V dt += + ⋅ += + + ∫∫ ∫ (2.13) 其中定义振荡器的相位增量为φex V ctrl = K V dt ∫ 。因此在锁相环电路中,压控振荡器是相位的 一个理想的积分器,其传递函数可以表示为, ( ) ex V ctrl K s V s φ = (2.14) M1 C1 C2 L1 I 1 Vb M1 C1 I 1 L1 C2 Vb M1 C1 C2 L1 I 1 V VDD DD VDD (a) (b) (c) 图 2.8 不同结构的单管振荡器

第二章电感电容压控振荡器 02 slope K, 00 巧 V 图2.9理想压控振荡器压控特性 压控振荡器电路设计主要有以下几个指标: 1)中心频率:振荡器的最大频率和最小频率的中间值od=(ox+omm)/2: 2)调谐范围:振荡器的最大频率与最小频率的差值(⊙x-om),通常情况下,也定义为 (ox-om)与中心频率0a比值的百分比形式(2(ox-om)/os+om)×100%; 3)调谐增益:压控振荡器的增益K,; 4)调谐线性度:理想压控振荡器的增益K,在整个调谐范围保持为常数,但是实际电路实 现的时候,往往不能够做到这一点。这就要求压控增益K,,在整个调谐范围内尽量保 持一个好的线性度。 5)相位噪声:载波频率频偏△o处,1Hz内单边带噪声谱密度与载波功率比值的分贝形式 (dBc/Hz),详细介绍参见第五章中的相位噪声定义。 6)输出信号频谱纯度:随着压控电压的改变,振荡波形不是一个理想的正弦波。为了使得 能量都集中在振荡器的基频上,我们设计的电路要尽量抑制高次谐波的存在。 7)输出电压幅值:从降低相位噪声方面来看,我们应该尽量使得输出的电压幅度大些,这 样可以降低压控增益Kv。特别是随着CMOS工艺的不断进步,电压不断降低的情况下, 提高输出电压幅值显得更加重要。 8)功耗:振荡器的功耗与相位噪声,输出电压幅度等密切相关,它们之间存在一定的权衡 和优化过程。CMOS工艺上实现振荡器的典型功耗为几个到几十个mW。 2.2.2窄带电感电容压控振荡器 在图2.6的交叉耦合负跨导电感电容振荡器等效电路中加入直流偏置Ial,可以得到图 2.10中的两种结构的振荡器电路2,3,4,5,6]。图2.10(a)中的负阻采用交叉耦合的NMOS对管 来实现,尾电流管Mn3为Mnl和Mn2管提供直流偏置。同样该结构也可以采用交叉耦合 的PMOS对管实现。在CMOS工艺上实现电感电容压控振荡器的最关键的问题是如何设计 和实现高性能的片上电感和片上可变电容。 目前情况下,片上电感的实现主要有三种:有源电感,键合线电感和片上螺旋电感。有 源电感的噪声性能比较差,在高频电路中一般不采用。键合线电感的品质因数比较高,通常 在1-2GHz可以达到50,但是其电感值偏差很大。片上螺旋电感是目前使用最为广泛的一种 电感,它最主要的优点是与CMOS工艺完全兼容,但是其品质因数比较低,一般在1-5GHz 电感电容压控振荡器 13
第二章 电感电容压控振荡器 电感电容压控振荡器 13 压控振荡器电路设计主要有以下几个指标: 1) 中心频率:振荡器的最大频率和最小频率的中间值 ( max min ) 2 ω ωω mid = + ; 2) 调谐范围:振荡器的最大频率与最小频率的差值(ω ω max min − ) ,通常情况下,也定义为 ( ) ω ω max min − 与中心频率ω mid 比值的百分比形式(2 100% (ωωωω max min max min − +× ) ) ; 3) 调谐增益:压控振荡器的增益 KV ; 4) 调谐线性度: 理想压控振荡器的增益 KV 在整个调谐范围保持为常数,但是实际电路实 现的时候,往往不能够做到这一点。这就要求压控增益 KV ,在整个调谐范围内尽量保 持一个好的线性度。 5) 相位噪声:载波频率频偏 ∆ω 处,1Hz 内单边带噪声谱密度与载波功率比值的分贝形式 (dBc/Hz),详细介绍参见第五章中的相位噪声定义。 6) 输出信号频谱纯度:随着压控电压的改变,振荡波形不是一个理想的正弦波。为了使得 能量都集中在振荡器的基频上,我们设计的电路要尽量抑制高次谐波的存在。 7) 输出电压幅值:从降低相位噪声方面来看,我们应该尽量使得输出的电压幅度大些,这 样可以降低压控增益 KV。特别是随着 CMOS 工艺的不断进步,电压不断降低的情况下, 提高输出电压幅值显得更加重要。 8) 功耗:振荡器的功耗与相位噪声,输出电压幅度等密切相关,它们之间存在一定的权衡 和优化过程。CMOS 工艺上实现振荡器的典型功耗为几个到几十个 mW。 2.2.2 窄带电感电容压控振荡器 在图 2.6 的交叉耦合负跨导电感电容振荡器等效电路中加入直流偏置 Itail,可以得到图 2.10 中的两种结构的振荡器电路[2,3,4,5,6]。图 2.10(a)中的负阻采用交叉耦合的 NMOS 对管 来实现,尾电流管 Mn3 为 Mn1 和 Mn2 管提供直流偏置。同样该结构也可以采用交叉耦合 的 PMOS 对管实现。在 CMOS 工艺上实现电感电容压控振荡器的最关键的问题是如何设计 和实现高性能的片上电感和片上可变电容。 目前情况下,片上电感的实现主要有三种:有源电感,键合线电感和片上螺旋电感。有 源电感的噪声性能比较差,在高频电路中一般不采用。键合线电感的品质因数比较高,通常 在 1-2GHz 可以达到 50,但是其电感值偏差很大。片上螺旋电感是目前使用最为广泛的一种 电感,它最主要的优点是与 CMOS 工艺完全兼容,但是其品质因数比较低,一般在 1-5GHz ωout Vctrl ω0 ω1 ω2 V1 V2 slope KV 图 2.9 理想压控振荡器压控特性