
在无限区间内的平均功率,定义为: 连续时间信号平均功率: R-号i0rh 离散时间信号平均功率: N P.lim 1x[nP
在无限区间内的平均功率,定义为: 连续时间信号平均功率: 离散时间信号平均功率: 1 2 lim | ( ) | 2 T T T P x t dt T ∞ →∞ − = 1 2 lim | [ ]| 2 1 N N n N P x n N ∞ →∞ =− = +

利用这些定义,就可以区分三种重要的信号: 1. 信号具有有限的总能量,即E<∞。这种信号的平 均功率必然为零,由平均功率的定义看出 p lim E T→∞2T 2.平均功率P有限的信号。根据上式,如果P。>0, 就必然有E∞=∞。因为,单位时间内有某一个非零 的平均能量(也就是非零功率),那么在无限区间 内积分或求和就必然得出无限大的能量值。例如常 数信号x[m=4就是无限能量,平均功率P=16。 (问:如果总能量已知是无限的,平均功率必有限?) 3.第三类信号就是E和P都不是有限的
利用这些定义,就可以区分三种重要的信号: 1. 信号具有有限的总能量,即 E ∞ <∞。这种信号的平 均功率必然为零,由平均功率的定义看出 2. 平均功率 P ∞ 有限的信号。根据上式,如果P ∞ >0, 就必然有 E ∞ =∞。因为,单位时间内有某一个非零 的平均能量(也就是非零功率),那么在无限区间 内积分或求和就必然得出无限大的能量值。例如常 数信号 x [ n]=4就是无限能量,平均功率 P ∞ =16 。 ( 问 :如果总能量已知是无限的,平均功率必有限?) 3. 第三类信号就是E ∞ 和 P ∞ 都不是有限的。 lim 0 T 2 E P T ∞ ∞ →∞ = =

12自变量的变换 信号与系统分析中一个重要的概念就是关于信号的 变换概念。例如,在飞机控制系统中对应于驾驶员 动作的信号,经由电的和机械的系统变换为在飞机 推力或飞机控制翼面(如舵或副翼)位置上的改 变,进而再经过空气动力学变换为在飞机速度和航 向上的变化。 本节将介绍几个最基本的信号变换,只涉及自变量 的简单变换,也就是时间轴的变换
1.2 自变量的变换 信号与系统分析中一个重要的概念就是关于信号的 变换概念。例如,在飞机控制系统中对应于驾驶员 动作的信号,经由电的和机械的系统变换为在飞机 推力或飞机控制翼面(如舵或副翼)位置上的改 变,进而再经过空气动力学变换为在飞机速度和航 向上的变化。 本节将介绍几个最基本的信号变换,只涉及自变量 的简单变换,也就是时间轴的变换
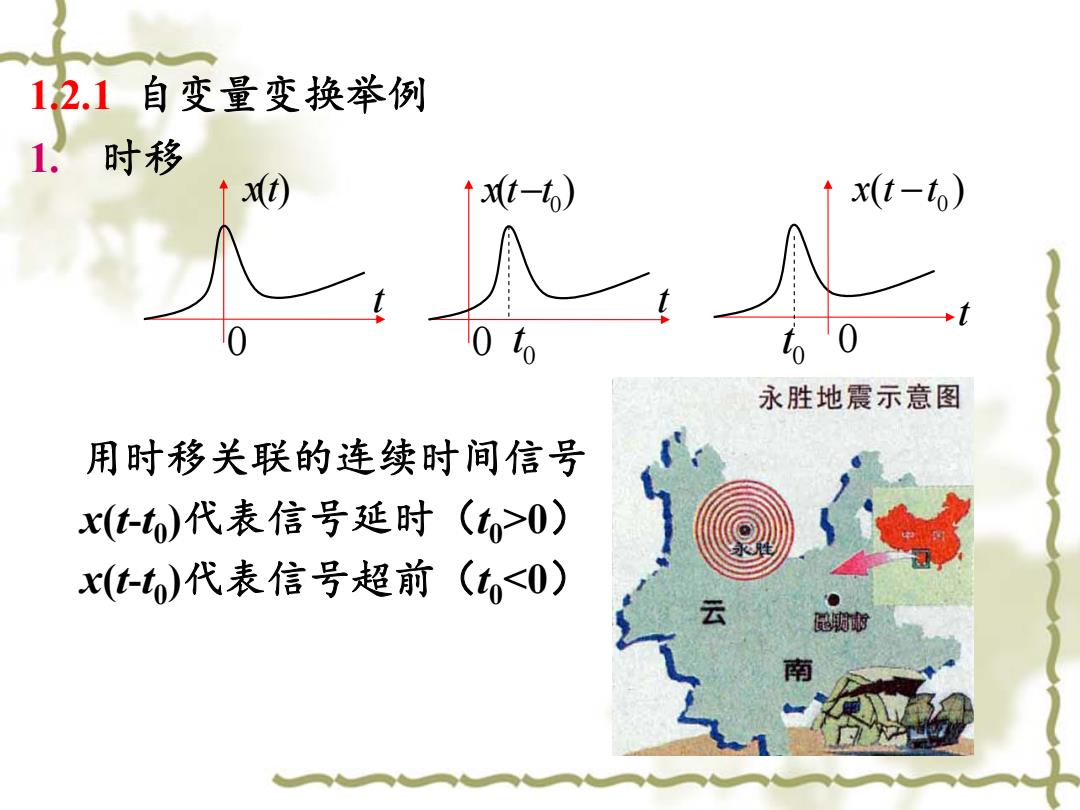
12.1自变量变换举例 1.时移 xt) ↑t-) x(t-t) to 永胜地震示意图 用时移关联的连续时间信号 x(t-)代表信号延时(>0) x(t-t)代表信号超前(t<0) 云
1.2.1 自变量变换举例 1. 时移 用时移关联的连续时间信号 x(t-t0 )代表信号延时(t0 >0) x(t-t0 )代表信号超前(t0 <0) )( 0 −ttx t 0 0t t 0 0t tx )( t 0 0 x( ) t t −
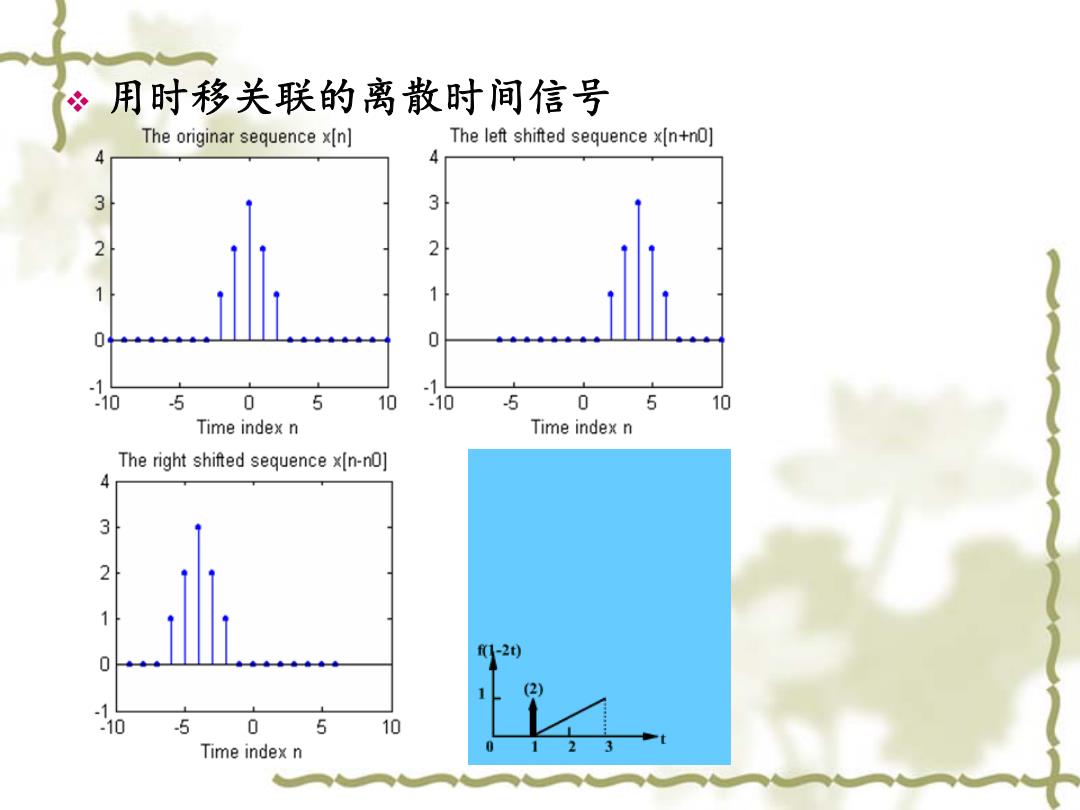
用时移关联的离散时间信号 The originar sequence x[n] The left shifted sequence x[n+nO] 3 3 2 2 1 0 0 、1 .10 5 0 5 10 -10 5 0 5 10 Time index n Time index n The right shifted sequence x[n-no] 4 3 2 f1-2t) 0 (2) -10 5 0 5 10 Time index n
用时移关联的离散时间信号