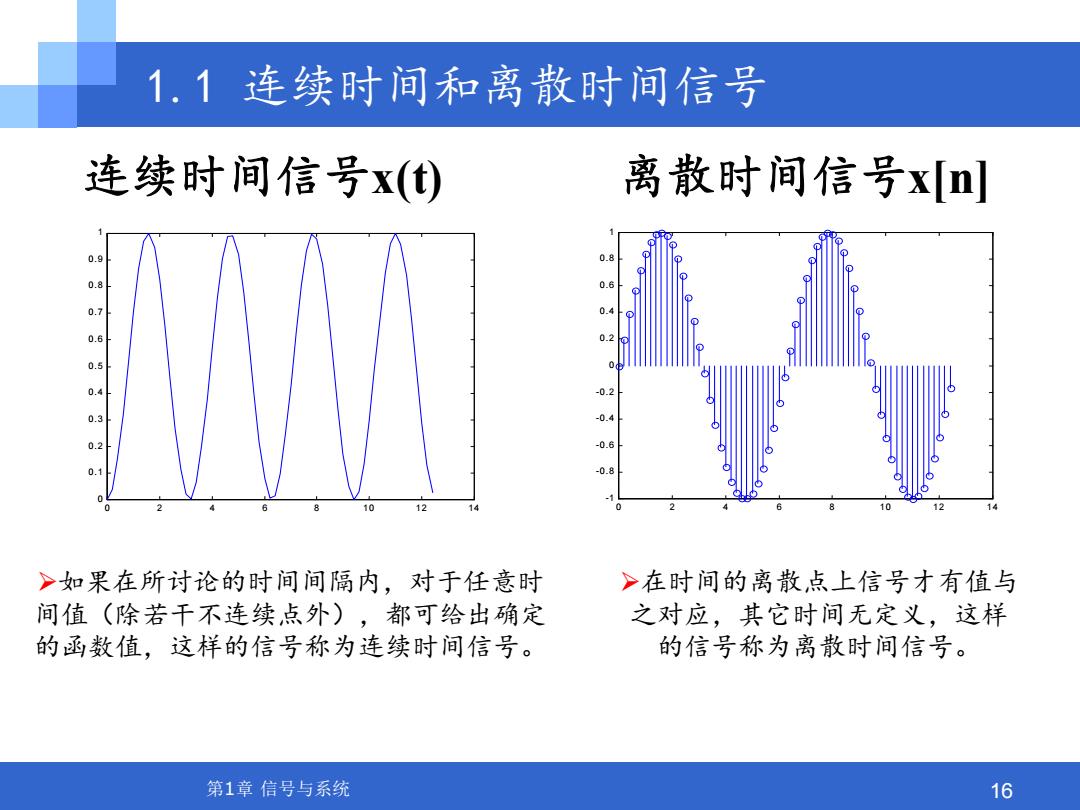
1.1连续时间和离散时间信号 连续时间信号x() 离散时间信号x[n] 0.9 0.8 0.8 0.6 0.7 0. 0.2 0.5 0 0.2 03 -0.4 0.2 0.1 0 0 12 10 >如果在所讨论的时间间隔内,对于任意时 >在时间的离散点上信号才有值与 间值(除若干不连续,点外),都可给出确定 之对应,其它时间无定义,这样 的函数值,这样的信号称为连续时间信号。 的信号称为离散时间信号。 第1章信号与系统 16
第1章 信号与系统 16 1.1 连续时间和离散时间信号 连续时间信号x(t) 0 2 4 6 8 10 12 14 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 0 2 4 6 8 10 12 14 -1 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 1 如果在所讨论的时间间隔内,对于任意时 间值(除若干不连续点外),都可给出确定 的函数值,这样的信号称为连续时间信号。 在时间的离散点上信号才有值与 之对应,其它时间无定义,这样 的信号称为离散时间信号。 离散时间信号x[n]
信号的图形表示: 我们将并行的讨论离散时间信号和连续时间信号 x(t) x(n] 连续时间信号x(t) 离散时间信号xm
信号的图形表示: 我们将并行的讨论离散时间信号和连续时间信号 t tx )( n nx ][ 连续时间信号 x(t) 离散时间信号 x[n]

11.2信号能量与功率 在很多应用中,信号是直接与在某一物理系统中具 有功率和能量的一些物理量有关的。 R 瞬时功率: =W00=R0=2r0 v() P (t) 在时间间隔t,≤≤,内消耗的总能量、平均功率就是: 44t0发oa R
1.1.2 信号能量与功率 在很多应用中,信号是直接与在某一物理系统中具 有功率和能量的一些物理量有关的。 瞬时功率: tv )( ti )( R )( 1 )()()()( 2 2 tv R tRititvtp === 在时间间隔t1≤t≤t2 内消耗的总能量、平均功率就是: = 2 1 2 1 )( 1 )( 2 t t t t dttv R dttp 2 2 1 1 2 21 21 1 11 () () t t t t p t dt v t dt tt ttR = − −

将电路的术语功率和能量引申开,我们就可以对任何 连续时间信号x()或离散时间信号x[采用类似的定 义,把信号在复数范围内定义,这样,一个连续时 间信号x()在t≤t≤2内的总能量就定义: fx(opa x记做x的模 t 其平均功率用t,-t,除就可得到。相类似,在n,≤n≤2 内的离散时间信号x[n的总能量就定义为: ∑nf 其除以n2-n1+1就得到 该区间的平均功率。 n=n 这里所谓的“功率”和“能量”是否与真正的物理量 相联系是无关的
将电路的术语功率和能量引申开,我们就可以对任何 连续时间信号 x ( t)或离散时间信号 x [ n ]采用类似的定 义,把信号在复数范围内定义,这样,一个连续时 间信号 x ( t) 在 t 1 ≤t ≤t2 内的总能量就定义: 其平均功率用 t2 - t 1 除就可得到。相类似,在 n 1 ≤n ≤n2 内的离散时间信号 x [ n ]的总能量就定义为: 2 1 2 )( t t dttx |x|记做x的模 2 1 2 | [ ]| n n n x n = 其除以 n2 - n1 +1就得到 该区间的平均功率。 这里所谓的“功率”和“能量”是否与真正的物理量 相联系是无关的

⑧在很多系统中,我们关心的是信号在一个无穷区间内 (-∞<tK+∞或-∞<<+∞)的功率和能量: 连续时间信号能量: E.=lim)d=()di 离散时间信号能量: E=lim∑1x[P-∑ln]P n=-N N=-00 对某些积分、求和可能不收敛,如x)或xl在全部时 间内都为某一非零的常数值就是这样。这样的信号具 有无限的能量,而E<∞的信号具有有限的能量
在很多系统中,我们关心的是信号在一个无穷区间内 ( - ∞ < t<+∞或 - ∞ <n<+∞)的功率和能量: 连续时间信号能量: 离散时间信号能量 : 对某些积分、求和可能不收敛,如 x ( t) 或 x [ n ]在全部时 间内都为某一非零的常数值就是这样。这样的信号具 有无限的能量,而 E ∞ <∞的信号具有有限的能量 。 2 2 lim | ( ) | | ( ) | T T T E x t dt x t dt +∞ ∞ →∞ − −∞ = = 2 2 lim | [ ]| | [ ]| N N n N n E xn xn ∞ ∞ →∞ =− =−∞ = =