卢瑟福: "It was quite the most incredible event that ever happened to me in my life.It was almost as incredible as if you fired a 15-inch shell at a piece of tissue paper and it came back and hit y0u.” 8000 太大了! 根据汤姆逊模型: 忽略电子的影响。 2Ze'r F= r<R 4π6R3 2Ze2 max 4nsoR2, r=R 0 R F=0.r>R 动量的变化等于冲量: pas=Fnax·Af= 1 2Ze2 2R 48R2
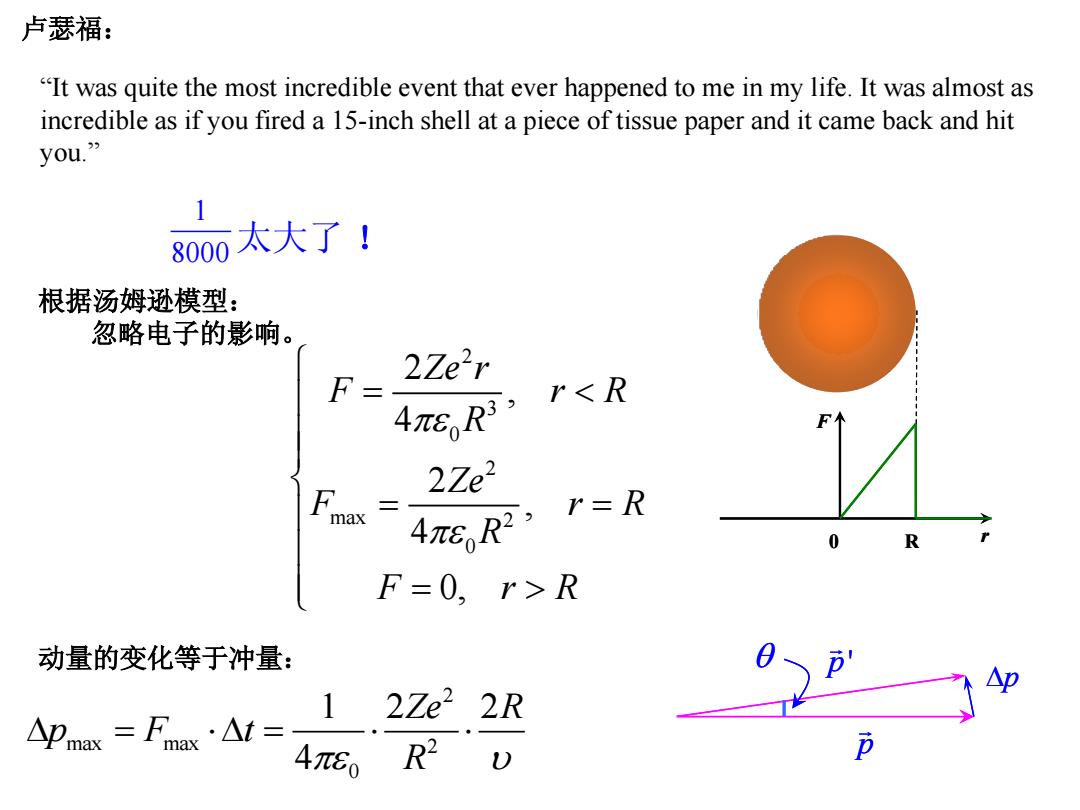
“It was quite the most incredible event that ever happened to me in my life. It was almost as incredible as if you fired a 15-inch shell at a piece of tissue paper and it came back and hit you.” 卢瑟福: 太大了 ! 1 8000 0 F R r 2 3 0 2 max 2 0 2 , 4 2 , 4 0, Ze r F r R R Ze F r R R F r R 根据汤姆逊模型: 忽略电子的影响。 p p ' p p p ' p 2 max max 2 0 1 2 2 4 Ze R p F t R 动量的变化等于冲量:
△pmax二 4Ze2 2e2 Z max 4π,RU24 4nER E 8s*29x10*2ad) 代入实验参数Z=79,E=5MeV,偏转角度只有0.026°。 多次散射? (0-0) 6=0 a-2a-j=小g 散射角度大于90°的概率小于10-3500! 无论如何都不可能出现大角散射的情况! 汤姆逊原子模型不正确!
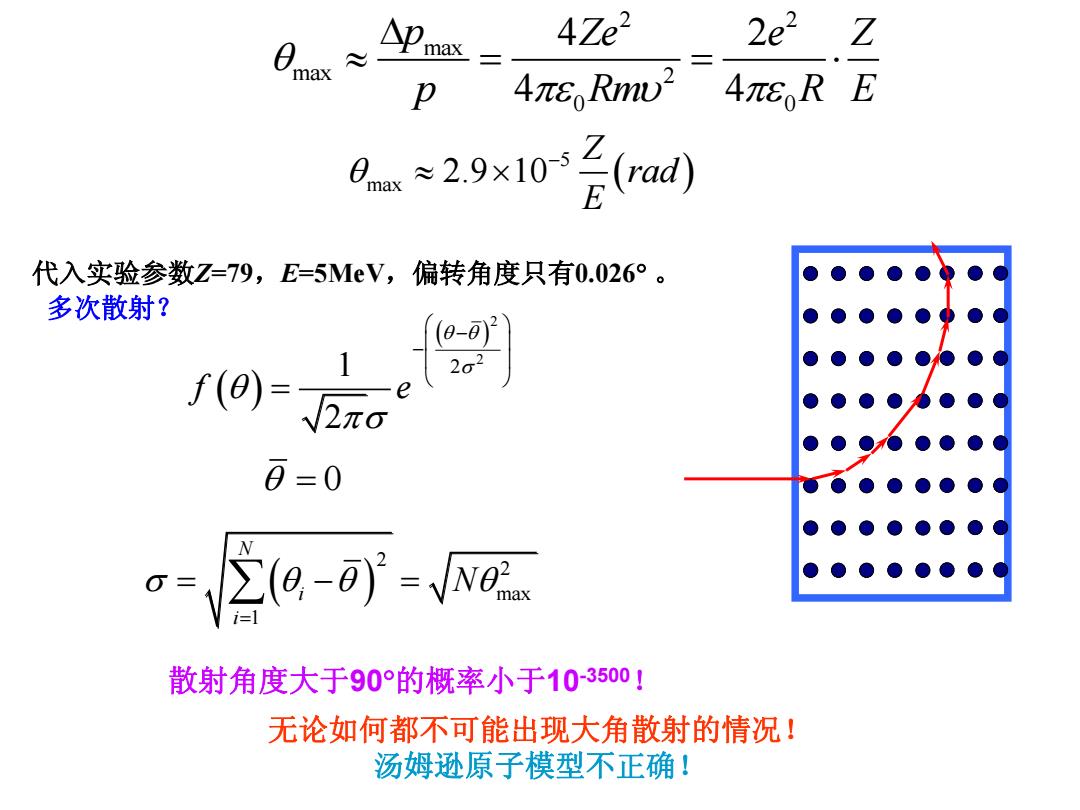
5 max 2.9 10 Z rad E 代入实验参数Z=79,E=5MeV,偏转角度只有0.026 。 多次散射? 2 2 1 2 2 f e 0 2 2 max 1 N i i N 散射角度大于90的概率小于10-3500! 无论如何都不可能出现大角散射的情况! 汤姆逊原子模型不正确! 2 2 max max 2 0 0 4 2 4 4 p Ze e Z p Rm R E
4Ze2 2e2 Z 0 max p 4πERU24πERE 原子中的所有正电荷和除了电子外的全部质 量都集中于中心非常小的区域内,这就是原子核 G粒子 原子核 电子 正电荷 原子核 电子 汤姆逊的原子模型 卢瑟福的原子模型
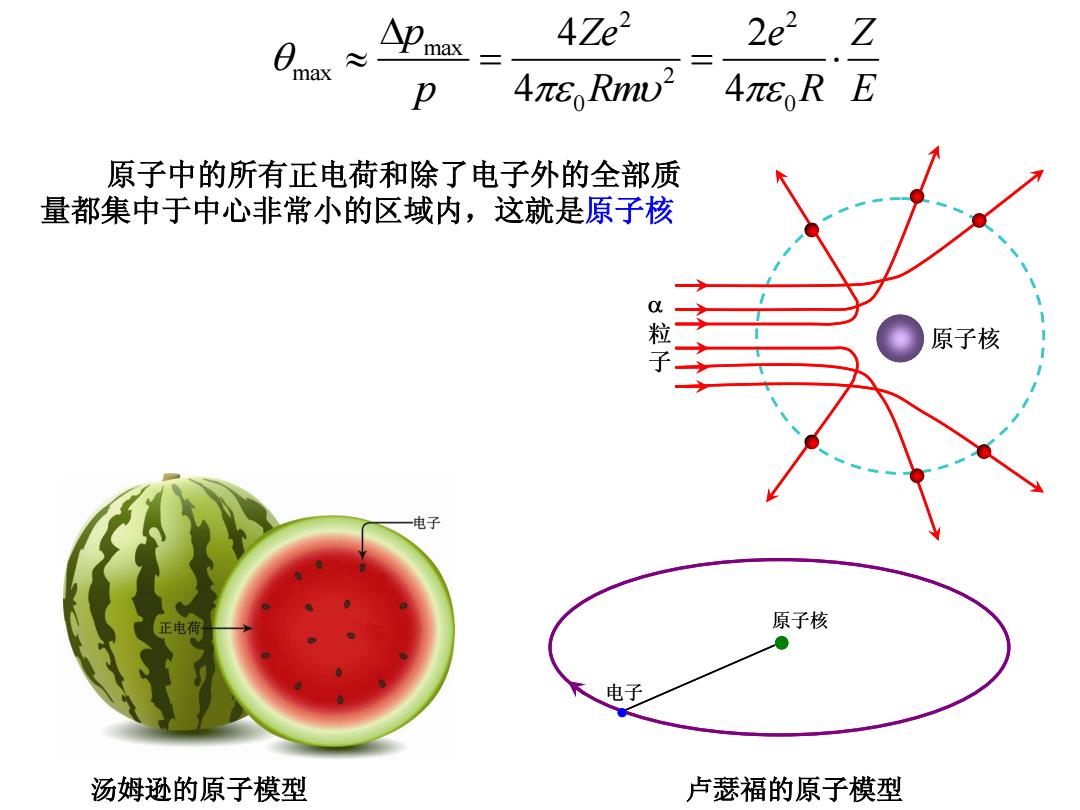
原子核 粒 子 2 2 max max 2 0 0 4 2 4 4 p Ze e Z p Rm R E 原子中的所有正电荷和除了电子外的全部质 量都集中于中心非常小的区域内,这就是原子核 汤姆逊的原子模型 原子核 电子 卢瑟福的原子模型

1.3.2卢瑟福散射公式 无穷远处垂直方向的速率: U.=Do sin0 Uo 粒子在垂直方向受力: F=Fsino= 1 zZe2 b 4,2 sino A 动量的改变等于冲 粒子与原子核散射的原理图 dv =Fdi-- zZe sinedt m r2 角动量守恒: 4π61m L=mr2 dp 二1 vob dt 11 do vb di zZe2 dv,=Arem sinpdo
F r b 0 A F F r b 0 A F 粒子与原子核散射的原理图 0 sin 2 2 0 1 sin sin 4 zZe F F r 2 2 0 F zZe sin d dt dt m m r 2 0 d L = mr = m b dt 无穷远处垂直方向的速率: 粒子在垂直方向受力: 动量的改变等于冲量: 角动量守恒: 2 0 1 1 d r b dt 2 0 0 sin 4 zZe d d m b 1.3.2 卢瑟福散射公式
n0=w.-0- zZe zZe2 4π6,mU, sin p(cos0) 散射角和瞄准距离的关系: 2b cot 2 D 到 dS 瞄准距离不可测量! 引入立体角: ds d2= 2 ds=sin OdOdo
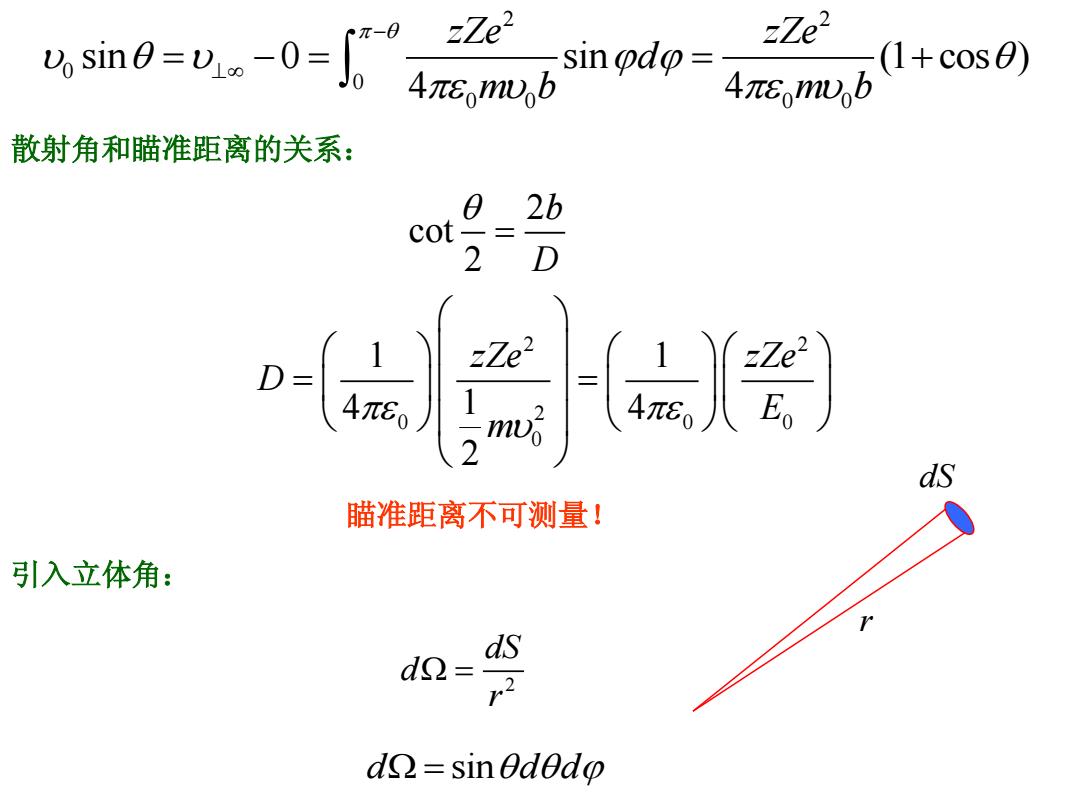
2 2 0 0 0 0 0 0 sin 0 sin (1 cos ) 4 4 zZe zZe d m b m b 2 cot 2 b D 2 2 2 0 0 0 0 1 1 4 4 1 2 zZe zZe D E m 散射角和瞄准距离的关系: 瞄准距离不可测量! 引入立体角: 2 dS d r dS r d d d sin