中国科学技术大学：《原子物理学》课程教学资源（课件讲稿）第一章 原子模型初探（主讲：朱林繁）

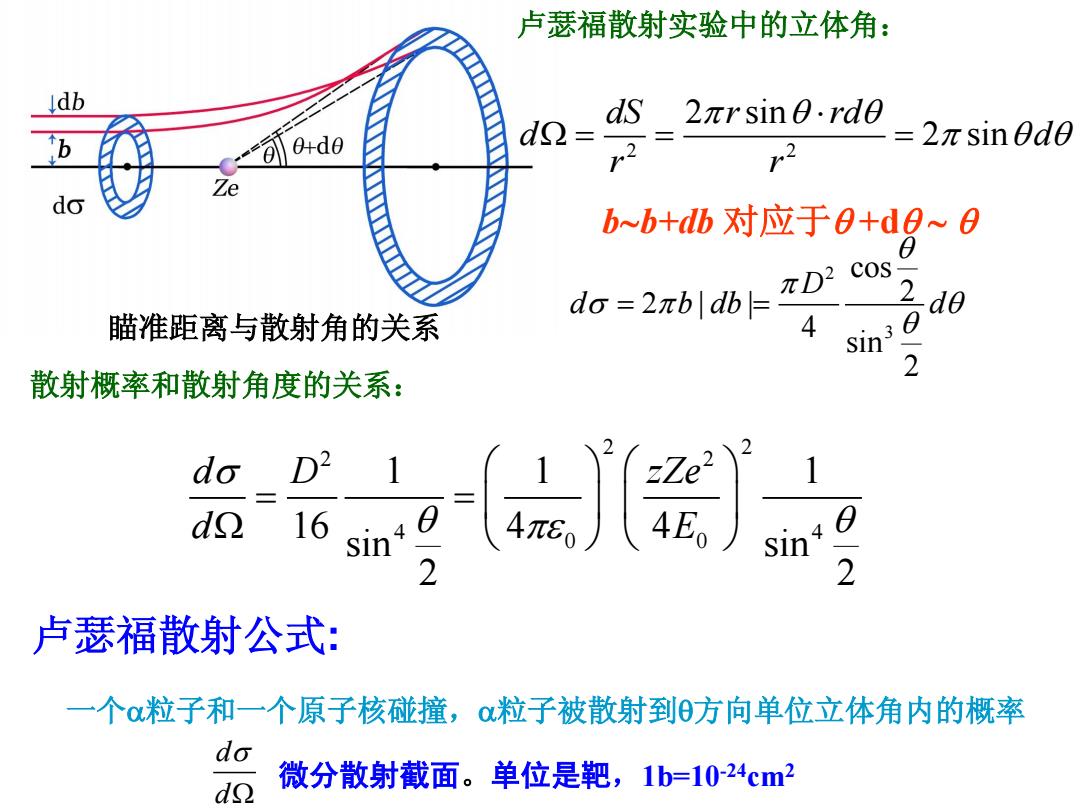
卢瑟福散射实验中的立体角： db ds 2πrsinθ.rd d= 2 r2 L=2πsin0d0 Ze do b~b+db对应于0+d0~0 8 πD2 COS do=2πb|db= 2d0 瞄准距离与散射角的关系 4 3 sin 2 散射概率和散射角度的关系： do D? dg 16 jj 1 40 sin 2 卢瑟福散射公式： 一个粒子和一个原子核碰撞，粒子被散射到方向单位立体角内的概率 do 微分散射截面。单位是靶，1b=1024cm2 dg

2 2 2 sin 2 sin dS r rd d d r r            bb+db 对应于 +d   2 3 cos 2 | | 4 sin 2 D d b db d          2 2 2 2 0 0 1 1 1 16 4 4 sin sin 2 2 d D zZe d E                      散射概率和散射角度的关系： 瞄准距离与散射角的关系 卢瑟福散射公式: 微分散射截面。单位是靶，1b=10-24cm2 d d   一个粒子和一个原子核碰撞，粒子被散射到方向单位立体角内的概率 卢瑟福散射实验中的立体角：

实际散射情况： dn do/S.m,·St=nNta2 do dg dΩ 积分截面： no dg 实际散射情况示意图 一个粒子入射与一个原子核散射的总概率

S0 n0 实际散射情况示意图 实际散射情况： 0 0 0 0 dn d d S/ n NS t n Nt d d d          积分截面： d d d       一个粒子入射与一个原子核散射的总概率

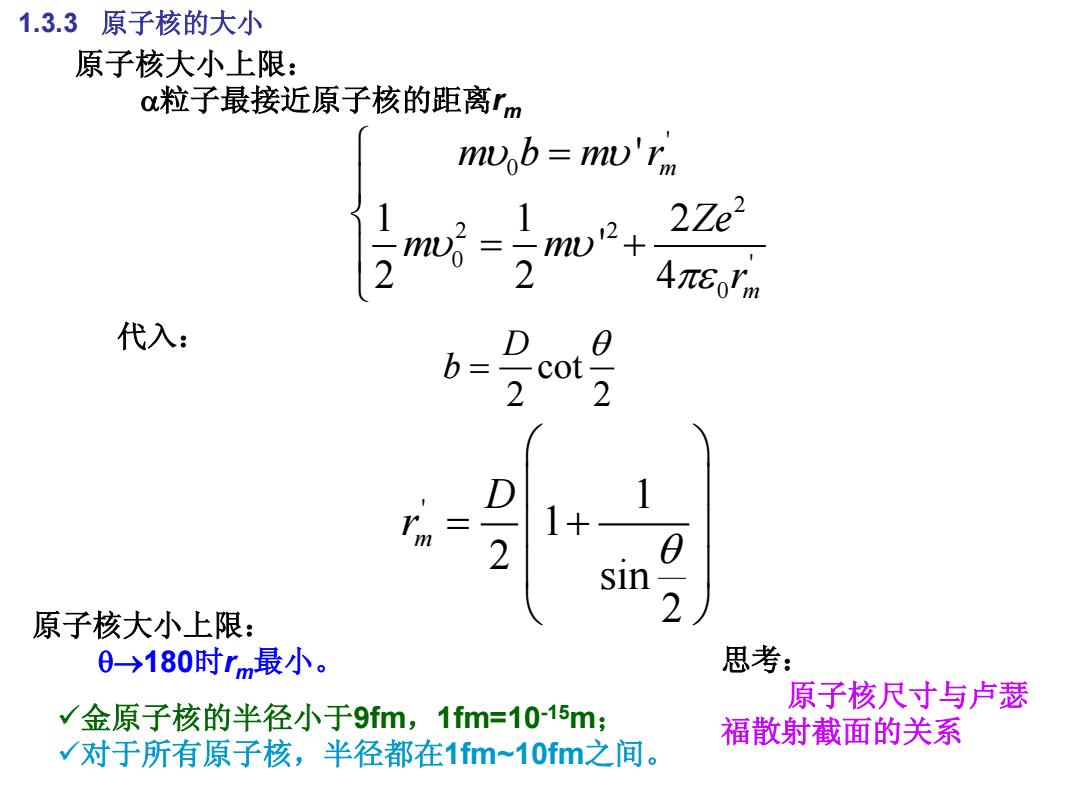
1.3.3原子核的大小 原子核大小上限： o粒子最接近原子核的距离rm 心b=mD'Tm 52Z 2Ze2 =-mu 2 4TEorm 代入： D b D 1 1+ 2 sin 原子核大小上限： 2 0→180时rm最小。 思考： 原子核尺寸与卢瑟 √金原子核的半径小于9fm,1fm=10-15m; 福散射截面的关系 √对于所有原子核，半径都在1fm~10fm之间

1.3.3 原子核的大小 ' 0 2 2 2 0 ' 0 ' 1 1 2 ' 2 2 4 m m m b m r Ze m m r              原子核大小上限： 粒子最接近原子核的距离rm cot 2 2 D b   代入： ' 1 1 2 sin 2 m D r            原子核大小上限：   180时rm最小。 金原子核的半径小于9fm，1fm=10-15m； 对于所有原子核，半径都在1fm~10fm之间。 思考： 原子核尺寸与卢瑟 福散射截面的关系

例子： 中国国土面积960万平方公里对应： 9.6×106km2≈1013m2 尺度 V103m=3.16×10m 按照原子核的尺寸和原子的尺寸比： 3.16×106×10-4m=316m 原子核与原子的尺度比 科大东区的1/6与中国国土的比

例子： 中国国土面积960万平方公里对应： 6 2 13 2 9.6 10 km 10 m   尺度 13 6 10 m 3.16 10 m   按照原子核的尺寸和原子的尺寸比： 6 4 3.16 10 10 m=316m    原子核与原子的尺度比 科大东区的1/6与中国国土的比

问题： 电子与原子散射截面的数量级？ 1.3.4卢瑟福原子模型 原子核 电子 卢瑟福的原子模型 卢瑟福原子模型所面临的原子塌缩问题及光谱问题

问题： 电子与原子散射截面的数量级？ e - 卢瑟福原子模型所面临的原子塌缩问题及光谱问题 1.3.4 卢瑟福原子模型 原子核 电子 卢瑟福的原子模型