
4月份的¥均库在额=100+86-93万元 5月份的¥均库存额86+10495万元 2 6月份的¥均库存额=104+14=109万元) 则第二手度的¥均库存额=93+95+109=9(万元 上述计算第二季度平均库存额的两个步骤,可以合并简化为: 100+8686+104,104+114 第二季度平均库存额= _93+95+109=99(万元) 3 上面计算过程概括为一般公式 g+0+a,+a+A+0 a=2 2 2 n-1 n-1 式中,ā表示序时平均数 a表示各项时点指标数值: n表示时点个数 根据上述计算公式,间隔相等间断时点数列的序时平均数等于首术项两指标数值之半 加中间各项指标数值,除以时点项数减一,所以称为“首尾折半法”。 ②间隔不等的间断时点数列。它是根据间隔不等的各期期初或期木时点资料编制的时 点数列。同样要假定向断的各时点之间的指标值是均匀变动的,山于各时点之间的向隔不等, 可用各个间隔的长度()为权数,对各相应时点的平均值进行加权平均,求待序时半均数。 计算公式为 +@+0+a5+A+a+af a-- 2 2 2 厂++A+f 例,根据表8-9资料计算2005年某商品的平均库存量 表8-9某商品2008年平均库存 时间1月初3月制 7月初 10月初 12月末 年存量(套) 1500 600 900 1600 1000 根据上表资料,计算某商品2005年的Ψ均库存量为:

1500+600×2+600+900×4+900+1600×3+1600+1000 ×3 =2 2+4+3+3 -=1062.5(套) 根据间断时点数列计算序时半均数,是假定两个相邻时点之间现象数量的变动是均今 的,而实际上各种现象不可能都是均匀变动的,故所得的结果只能是一个近似值。如果时点 数列的间隔越小,则所求得的结果越接近实际。因此,间断时点数列的间隔不宜太长。 2.根据相对数动态数列计算序时平均数 山于相对数动念数列是派生数列,不能用相对指标时向数列的各个指标数值直接相加除 以项数来求得,而要利用其相应的两个绝对数动念数列,分别计算分子数列的序时半均数无 分母数列的序时半均数,而后加以对比,即可求得。其基本计算公式为:。=日 计算时,应先分析对比的分子和分母是时期数列还是时点数列,是哪一种时点数列,然 后再按照前面所述的相应公式计算。具体有三种情形: 1)分子和分母均为时期数列。则有: c=a∑0,∑b∑a ∑b 上式中,需根据所掌握的资料个同采取不同的计算,当所掌握的资料不全时,即 b,c有缺项时,同样可以计算 0c= .a=bc代入上式,得:c= ∑bc 这个公式实际就是加权算述平均数公式。 这个公式实际就是加权调和平均数公式 根据所掌握的实际资料来确定选用哪个公式,三个公式的计算结果应完全相同 例,某企业第一季疫产量计划完成情况如表8-10所示。 表8-10某企业产品第一季度产量完成情况表 时间 一月 _日 实际产(吨 420 714 b计划产量(吨 400 500 700 c计划完成(%) 105 112 102 c= ∑a420+560+714 ∑b 400+500+700 =1.059=105.9% ∑6c_400×105%+500×112%+700x102% =1.059=105.9% ∑b 400+500+700

2004 20052006 200720 a第=产业从业人员数(百人 15456 16851 1790 1837 18679 b全部从业人员数(百人) 67199679476885069600 69957 C第产业从业人员所占比重(%)23.024.826.026.426.7 420+560+714 是0的.+i2%+o2 420.560.714 =1.059=105.9% 2)分子和分母均为时点数列。山于时点数列计算序时半均数,有连续与间断之分,而每 种又有间隔相等和间隔不等之分,这就形成四种不同的情况,但其基本的计算方法不变。现 以最常见的间隔相等间断时点数列对比所形成的相对指标和间隔不 等的间断时点数列对 比所形成的相对指标时间数列序时平均数的计算为例,说明其一般的计算方法。 (1)时间间隔相等间断时点数列。对于该数列,根据前边的基本思路,可采用下公 式: 2 a-a n-1 2+4+n+号 n-1 当所掌程的资料不全时,可将a=bc及b=“代入上式,即可得出两个变形公式为 -g空66+M+g 表8-11菜地区2004一2008年末第三产业从业人员情况表 根据表8-11的资料,某地区2002一2006年间第三产业从业人员数占全部从业人员数的 年平均比重为: 15456+16851+17901+18375+18679 =6799+67947+68850+6960016995725.53% 2 2 若用两个变形公式计算,则: 6719×0.23+67947×0.248+6850x0.26+69600x0.264+69957x0.267 c-2 =25.53% 6719+67947+6850+69600+6957 2 15456+16851+17901+18375+18679 度c=1545616851,17901,1837518679=25.53% 2×0.23+0.248+0.26+0.2642×0.267

(2)时间间隔不等间断时点数列。如果间隔不等,则要用各个间隔长度作权数,用加 权半均法计算分子和分母的序时平均数,然后再对比。其计算公式为: +aj+a+af+A+a+af)÷∑f 2 色+6万+6+6万+A+b+b)+∑f 3)分子和分母为不同性质的时期数列和时点数列。其基本公式不变,仪分子数列和分 母数列的序时平均数的计算方法,应依据数列的具体性质、类别而定。举例如下: 表8-12莱地区208年第三季度各月商品流转次 月 6月 7月 8月 9月 a盛品清传额(万元) 144.0 148.2 154.7 b月末商品存领(万心) 64.2 51.0 47.8 52.0 c商品流转次数 3.1 要求计算该商场第二季度平均商品流转次数和第二季度商品流转次致。 山于商品销售额是时期指标,月木商品年存额是时点指标,故两者个能直接比较,需求 出各月华均商品库存额,能对比求出各月的商品流转次数。计算第一季度月半均商品流封 次数,不能直接将各月的商品流转次数相加平均,而应按照基本公式分别求出分子数列和分 母数列的序时平均数, 再对比求得 d 1440+148.2+154.7 =2.848 言+6+6+ 64.2 52.0 +51.0+47.8+ 13 /(4-1) 计算第三季度商品流转次数,同样也不能将各月的商品流转次数直接加总,它等于第 季度的商品销售总额除以第一季度月平均商品库存额:或等于第一季度的月平均商品流转次 数乘以月数。即: 第三季度商品流转次数 ∑a 144.0+148.2+154.7 =8.544 b 42+51.0+47.8+520 3 或者2.844×3=8.544(次) 3.根据平均数动态数列计算序时平均数 平均指标时间数列可分为一般平均数时向数列和序时半均数时间数列两种 1)山 平均数组成的平均指标时间数列 实际上山是两个总量指标 数列对比形 成的,其方法和山相对数动念数列计算子时平均数的方法基本相同,即分别计算分子数列无 分母数列的序时平均数,然后将这两个序进平均数进行对比,就可求得这两个平均数动态数 列的序时平均数。其中分子是标志总量数列,通常为时期数列,分母是总体单位总数数列, 一般为时点数列,比且体计算方法可参照前例中半均商品流转次数的计算 2)山序时平均数组成的平均指标时间数列计算子时平均数,在时期相等时,可直接采 用简单算术平均法来计算:如时期不相等,则可以时期为权数,采用加权算术平均法计到 例,某商场2005年第二季度各月半均商品库存额表8-12所示。 表8-13某商场2008年第二季度平均各月商品库存额 月份 4月 5月 6月 平均商品存额(万元 57.6 44 49.9
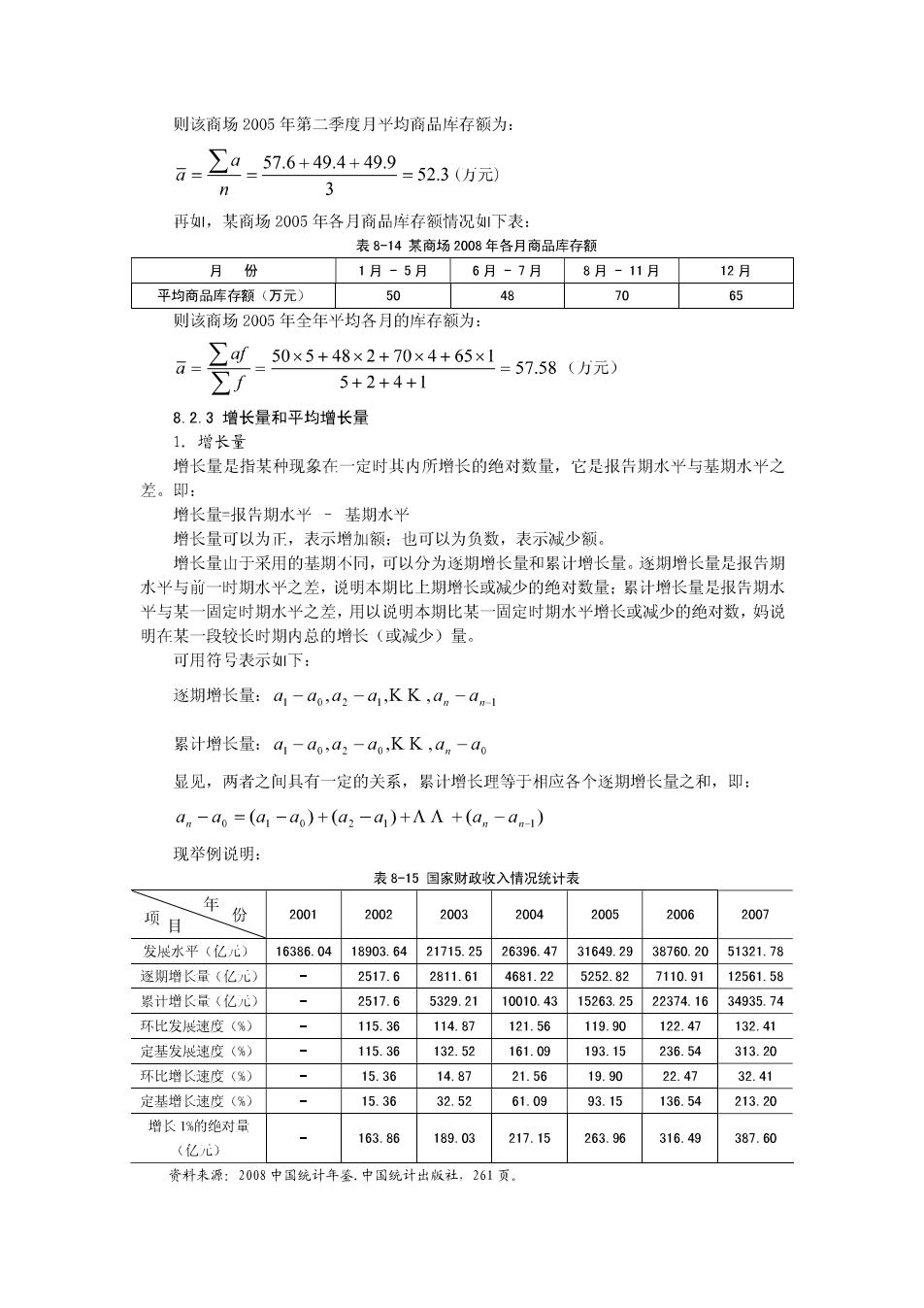
则该商场2005年第二季度月华均商品存额为: 石=2_576+494+499=52305元 3 再如,某商场2005年各月商品库存额情况如下表: 表8-14某商场2008年各月商品库有面 月 1月-5月6月-7月8月-11月 12月 平均商品库存额(万元 50 48 70 65 则该商场2005年全年业均各月的库存额为: ag0x5+4将x2+0x4+651.5758(内元 ∑f 5+2+4+1 82.3增长景和平均增长 1.增长里 增长量是指某种现象在一定时比内所增长的绝对数量,它是报告期水华与基期水华之 差。即: 长量报告期水业一基期水华 增长量可以为正 表示增加额 也可以为负数,表示减少额。 增长量山于采用的基期不同,可以分为逐期增长量和累计增长量。逐期增长量是报告期 水平与前一时期水平之差,说明本期比上期增长或减少的绝对数量:累计增长量是报告期水 平与某一固定时期水平之差,用以说明本期比某一固定时期水平增长或减少的绝对数,妈说 明在某一段较长时期内总的增长(或城少)量 可用符号表示如下: 逐期增长量:a,-ao,a2-a,KK,an-a 累计增长量:a-ao,a2-aKK,a。-a 显见,两者之间具有一定的关系,累计增长理等于相应各个遂期增长量之和,即: a,-ao =(a-ao)+(a;-a )+AA +(a,-a) 现举例说明 表8-15国家财政收入情况统计表 项目 年粉 2001 202 2003 2004 2005 2006 207 发展水平(亿心】 16386.04 18903.64 21715.2 26396.4731649.29 38760.20 51321.78 逐期增长量(亿元)》 2517.6 2811.61 4681.225252.82 7110.91 12561.58 累计增长量(亿元) 25176 532921 10010.4315263.2522374.16 3493574 环比发烘速府 115.36 14.87 121.56 19.90 2247 13241 定基发投速度(% 115.36 132.5 161.09 193.15 236.54 313.20 环比增长速度(%) 15.36 14.87 21.56 19.90 22.47 32.41 定基增长速度(%》 15.36 32.52 61.09 93.15 136.54 213.20 增长1%的绝对司 163.86 189.03 217.15 263.96 316.49 387.60 货来源:2008中国就计年,中国统计出版社,261页