案例 在一项临床实验中,试验药组在用药前的血 红蛋白的值(g机)如下所示,请问其平均水 平如何 7159 118 136 155 126 110 122 14 125 144 135 147 156 139 116 131 137 163 139 122 94 156 的 159 156 121 165 138 86 145 132 133 146 118 120 127 153 115 141 140 135 129 136 140 138 139 146 128 144 140 132 123 98 144 125 152 123 144 193 131 124 122 139 129 168 160 135 149 166 147 138 131 1
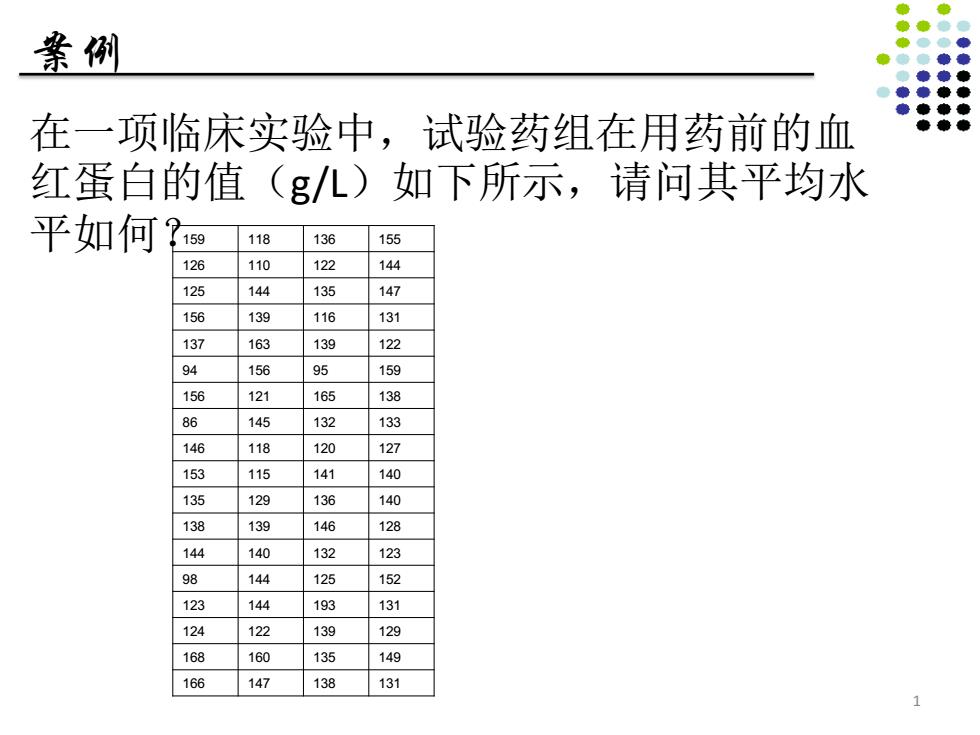
案例 在一项临床实验中,试验药组在用药前的血 红蛋白的值(g/L)如下所示,请问其平均水 平如何? 1 159 118 136 155 126 110 122 144 125 144 135 147 156 139 116 131 137 163 139 122 94 156 95 159 156 121 165 138 86 145 132 133 146 118 120 127 153 115 141 140 135 129 136 140 138 139 146 128 144 140 132 123 98 144 125 152 123 144 193 131 124 122 139 129 168 160 135 149 166 147 138 131

均数Mean 适用条件:资料呈正态或近似正态。 可用于反映一组成对称分布的变量值在数量上的 平均水平 Σ为求和符号,读成sigma 灭=X+X,++X2= ∑X n n
均数Mean n X n X X X X n S = + + + = 1 2 ! 适用条件:资料呈正态或近似正态。 可用于反映一组成对称分布的变量值在数量上的 平均水平 Σ为求和符号,读成sigma 2
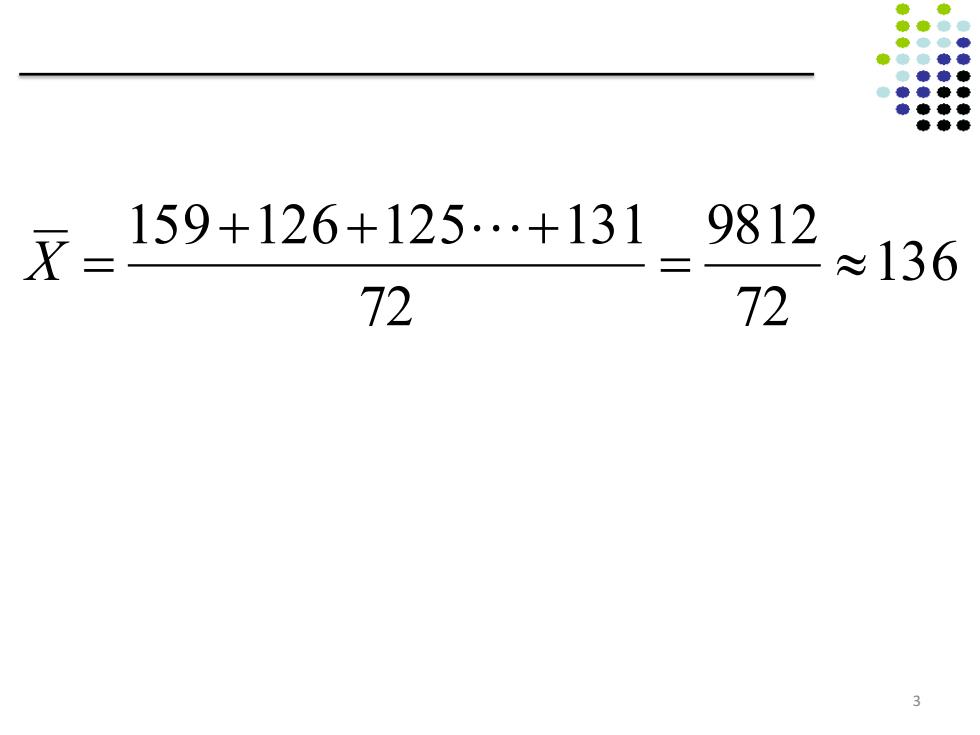
◆ 159+126+125+1319812 ≈136 72 72 3
3 136 72 9812 72 159 126 125 131 = » + + + = ! X
均数Mean 适用条件:资料呈正态或近似正态。Σ 为求和符号,读成sigma X=+方XfX,+.+fX_X f+方+∫++f f 频数 组中值=[(本组下限+本组上限)/2] “权数”:权衡各组段组中值由于频数 不同对均数影响的作用
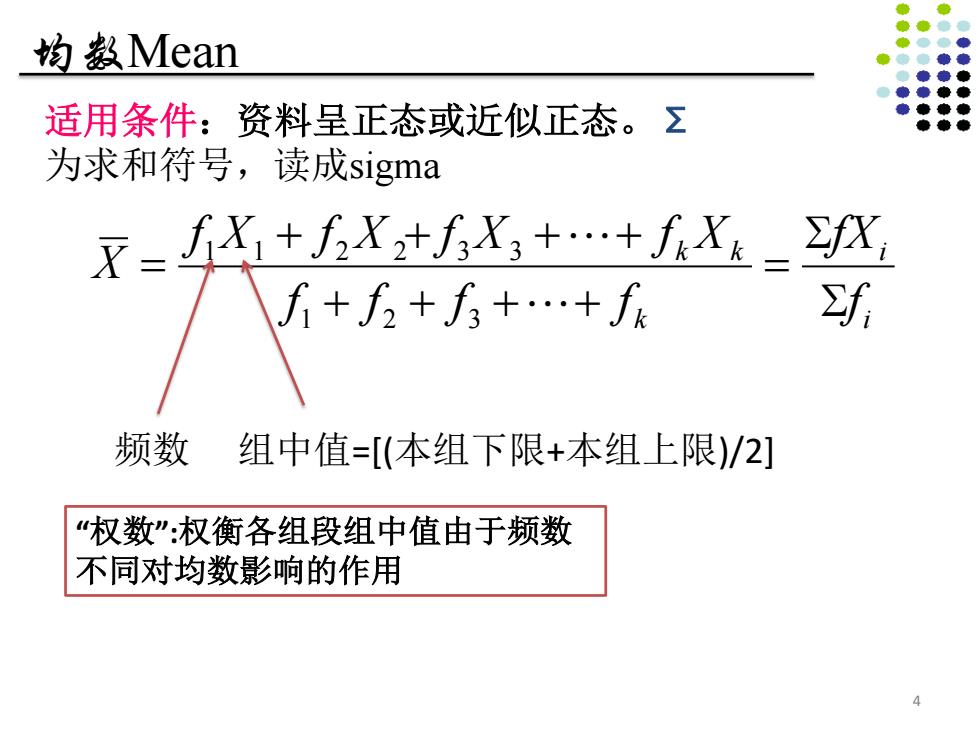
均数Mean i i k k k f fX f f f f f X f X f X f X X S S = + + + + + + + + = ! ! 1 2 3 1 1 2 2 3 3 适用条件:资料呈正态或近似正态。Σ 为求和符号,读成sigma 频数 组中值=[(本组下限+本组上限)/2] 4 “权数”:权衡各组段组中值由于频数 不同对均数影响的作用
均数Mean 组段 频数, 组中值,X X ● (1) (2) (3) (4)=(2)×(3) 85-95 2 90 180 95-105 y 100 200 105-115 1 110 110 115-125 13 120 1560 125-135 13 130 1690 135-145 22 140 3080 145-155 8 150 1200 155-165 8 160 1280 165-175 2 170 340 均数= 175-185 0 180 0 (9830/72) 185-195 1 190 190 ≈136 合计 9830 5
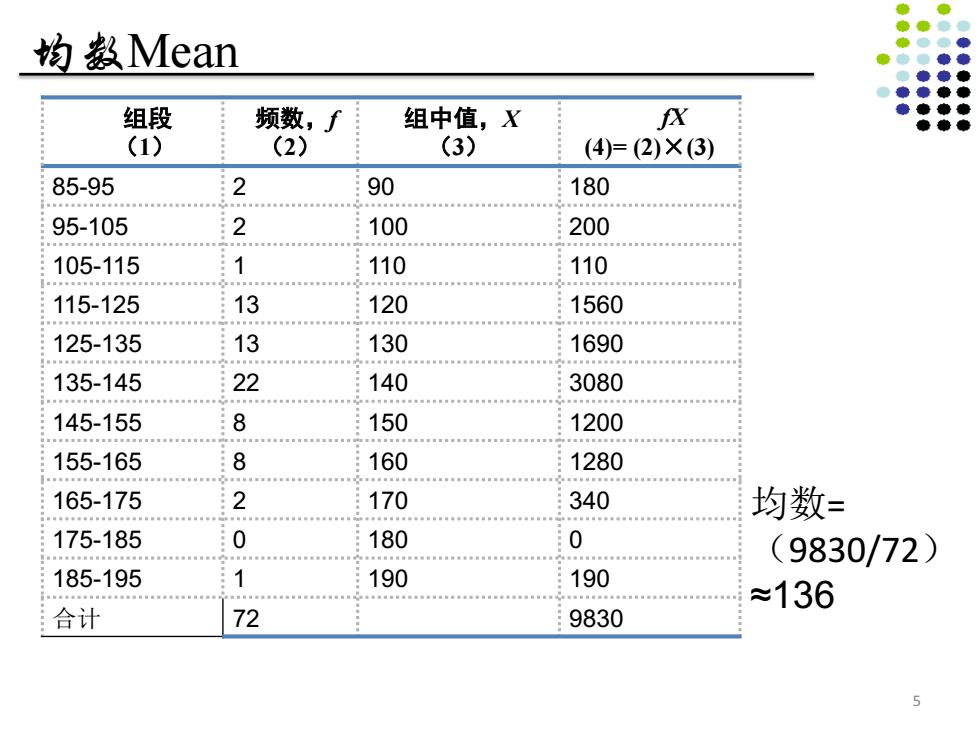
均数Mean 组段 (1) 频数,f (2) 组中值,X (3) fX (4)= (2)×(3) 85-95 2 90 180 95-105 2 100 200 105-115 1 110 110 115-125 13 120 1560 125-135 13 130 1690 135-145 22 140 3080 145-155 8 150 1200 155-165 8 160 1280 165-175 2 170 340 175-185 0 180 0 185-195 1 190 190 合计 72 9830 均数= (9830/72) ≈136 5