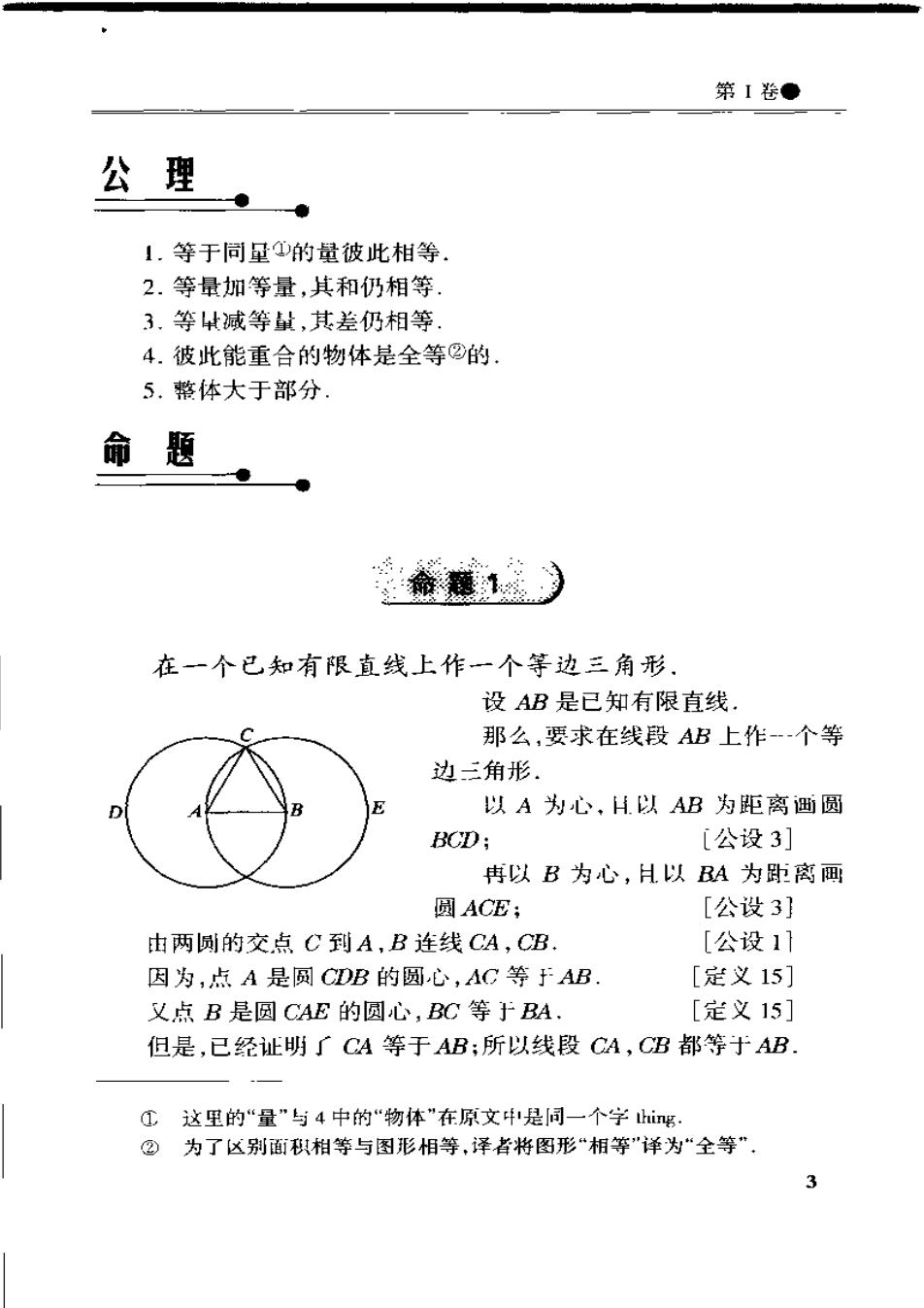
第1卷● 公理 1.等于同量的量彼此相等 2.等量加等量,其和仍相等 3.等减等封,其差仍相等 4.彼此能重合的物体是全等②的 5.整体大于部分 命题 裔薄远) 在一个已知有限直线上作一个等边三角形 设AB是已知有限直线 那么,要求在线段AB上作.个等 边三角形 以A为心,H以AB为距离画圆 BCD; [公设3] 冉以B为心,H以A为即离画 圆ACE; [公设3] 由两圆的交点C到A,B连线CA,CB. [公设11 因为,点A是圆CDB的圆心,AG等于AB [定义15] 义点B是圆CAE的圆心,BC等于BA. [定义15] 但是,已经证明了CA等于AB;所以线段CA,CB都等于AB ①这里的“量”与4中的“物体"在原文中是同一个学hig. ②为了区别面积相等与图形相等,译者将图形“相等“详为“全等” 3

●欧几甲得·儿何原木 而H等于同量的量彼此相等 [公理1] 二条线段CA,AB,BC彼此相等. 所以.角形A是等边的,即在已知有限直线AB上作出了这个 一角形 这就是所要求作的. 命瓶2) 由一个已知,点(作为端点)作一线段等于已知线段 设A是已知点,℃是已知线段, 那么,要求由点A(作为端点)作一线段 等于已知线段BC. H 由点A到点B连线段AB,[公设1] 而且在AB上.作等边二角形DAB,I.1]O 延长DA,DB成直线AE,BF,[公设2] 以B为心,以BC为距离画圆CGH. [公设3】 再以D为心,以DG为距离画圆G辽. 【公设31 因为点B是圆CGH的心,故BC等于BG [定义15] H点D是圆GL的心,故DL等于DG. [定义15] 又DA等于DB,所以余量AL等余世BG [公理31 但已证明了BC等于BG,所以线段AL、BC的每·个都等于BG 又因等丁同量的量彼此相等 [公理] 所以,AL也等JBC. 从附,由已知点A作出了线段AL等」已知线段BC. 这就是所要求作的. ①[.1]表示第I卷,第1个命题,此后均如此

第1卷● 已知两条不相等的线段,试由大的上边截取一条线段使 它等于另外一条. 设AB,C是两条不相等的线段,且AB大 下C. 这样要求由较大的AB上截取一段等于 较小的C. 由点A取AD等于线段C,[I.2] 且以A为心,以AD为距离画圆DEF, [公设3] 因为点A是圆DEF的圆心,故AE等于 AD. [定义15] 但C也等于AD,所以线段AE、C的每一条都等于AD;这样,AE 也等于C. [公理1] 所以,已知两条线段AB、C,由较大的AB上截取了AE等于C, 这就是所要求作的. 4 如果两个三角形中,一个的两边分别等于另一个的两边, 而且这些相等的线段所夹的角相等.那么,它们的底边等于底 边,三角形全等于三角形,这样其余的角也等于相应的角,即 那些等边所对的角」 设ABC,DEF是两个三角形,两边AB,AC分别等于边DE、DF, 即AB等于DE,且AC等于DH',以及角BAC等于角EDF. 5

●欧几甲得·儿何原本 则可证底BC也等于底,角形 ABC全等于:角形DEF,其余的角分别 等于其余的角,即这此等边所对的角,也 就是角ABC等于角DEF,H.角ACB等 于角DE. 如果移动三角形AB℃到二角形 DEF上.,若点A洛在点D上且线段AB落在DE上,因为AB等于DE. 那么,点B也就与点E重合. 又,AB与DB重合,因为角BAC等于角EDF,线段AC也与DF 重个. 囚为AC等于DF,故点C也与点F重合 但是,B也与E重合,故底BC也与底F重合 「事实上,当B与E重合月C与P重合时,底BC不与底EF重合 则二条直线就围成一块空间:这是不可能的,所以底O就与EF重 合]二者就相等 公理4] 这样,整个一三角形ABC与整个三角形DP重合,于是它们全等 且其余的角也与共余的角重合,是它」都相等,即角ABC等于 角DEF,且角ACB等于角DFE 这就是所要证明的 金题5之) 在等腰三角形中,两底角彼此相等,并且若向下延长两 腰,则在底以下的两个角也彼此相等 设ABC是一个等腰二角形,边AB等于边AC,H延长AB,AC成 直线BD,CE 公设2] 则可证角ABC等于角ACB,凡角CBD等于角BE, 在BD上任取·点F,且在较大的AE上截取一段AG等于较小的 AF, [1.3] 连接FC和GB。 [公设1] 6

第1卷意 因为AF等于AG,AB等于AC,两边FA、AC分 别等于边GA、AB,且它们包含着公共角FAG 所以底FC等于底GB,且一角形AFC仑等于三 角形AGB,其余的角也分别相等,即相等的边所对的 角,也就是角ACF等于角ABG,角AFC等于角 AGB. [1.4] 又因为,整体AF等于整体AG,且在它们中的 AB等于AC,余啦BF等于余量CG」 「公理3] 但是已经证明了FC等于GB; 所以,两边BF、C分别等于两边CG、GB,且角BFC等于角CGB. 这里底BC是公用的;所以,三角形BFC也全等于三角形CGB; 又,其余的角也分别相等,即等边所对的角 所以角FBC等于角GCB,且角BCF等于角CBG 出以上已经证明了整个角ABG等于角ACF,且角CBG等于角 BCF,其余的角ABC等于其余的角ACB [公理3] 又它们都在三角形ABC的底边以上。 从而,也就证明了角BC等于角GCB,且它]都在三角形的底边 以下. 证完 命瓶发 如果在一个三角形中,有两角彼此相等,则等角所对的边 也彼此相等 设在二角形ABC中,角ABC等于角ACB 则可证边AB也等于边AC. 若AB不等于AC,其中必有~个较大,设AB 是较大的:由AB上截取DB等于较小的AC. [1.3]