
1组内观察值数目相等的单向分组资料的方差分析 d.计算F值(列出方差分析表) 方差分析表 变异来源 自由度DF 平方和SS 均方MS F值 处理间 K-1 SS S2=SS:/df F=S2/S2 误差 K(n-1) SSe Se2=Sse/df2 总变异 nk-1 SS 平方和 自由度 均方 F(3,12) F0.05 SSt=504 3 St2=504/3=168S21Se2=20.56* 3.49 SSe=SST-SSt=98 12 S。2=98/12=8.17 F0.01 SST=602 15S,2=602/15=40.13 5.74
方差分析表 平方和 自由度 均方 F(3,12) F0.05 SSt=504 3 St 2=504/3=168 St 2 / Se 2=20.56** 3.49 SSe=SST-SSt=98 12 Se 2=98/12=8.17 F0.01 SST=602 15 ST 2=602/15=40.13 5.74 变异来源 自由度DF 平方和SS 均方MS F值 处理间 K-1 SSt St 2= SSt /df1 F=St 2 / Se 2 误差 K(n-1) SSe Se 2= Sse /df2 总变异 nk-1 SST d.计算F值(列出方差分析表) 1.组内观察值数目相等的单向分组资料的方差分析
1组内观察值数目相等的单向分组资料的方差分析 e.多重比较 。计算平均数的标准误$E= Se2 8.17-143 4 ·采用新复极差法, 查SSR表, 自由度为12时 平均数大小排序、比较 p 2 3 4 处理苗高 显著性 SSRo.o5 3.083.233.33 0.05 0.01 SSR0.01 4.32 4.55 4.68 D 29 a A 4.40 4.624.76 B 23 b AB LSRo.05 A18 C BC LSR0.01 6.18 6.516.69 C.14 C f结论 本试验中不同处理间有极显著差异(F值20.56>Fo1值 (5.47)),其中在.05水平上D处理与其他处理有显著 差异,B处理与A、C处理有显著差异。在.01水平D 处理与A、C处理间有显著差异,B处理与C处理有显 著差异。其他处理间差异均不显著
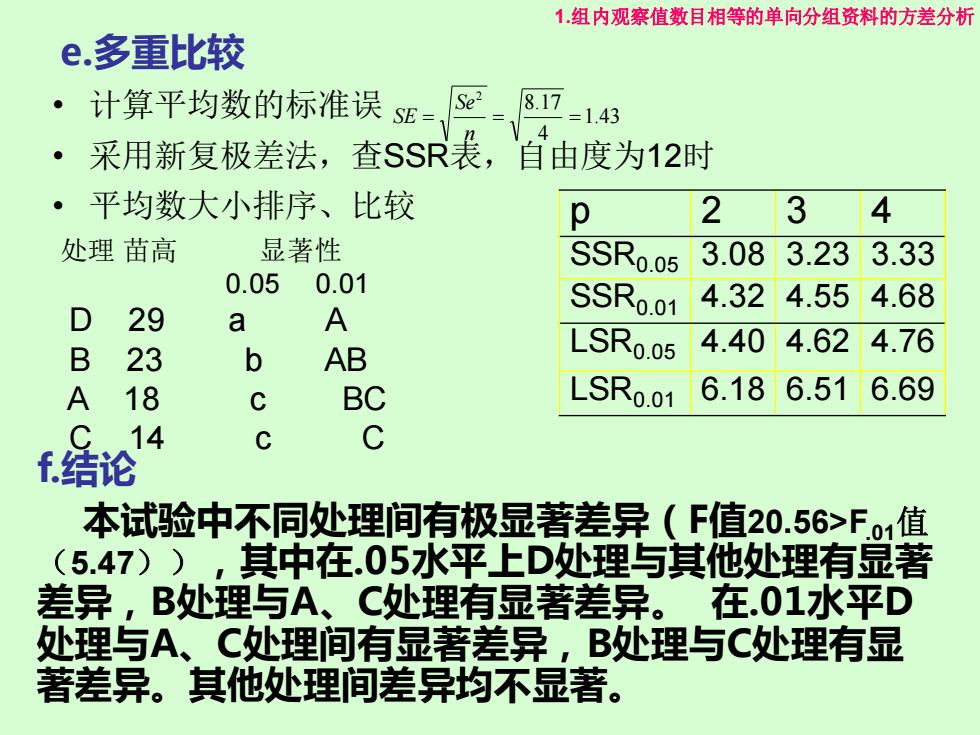
• 计算平均数的标准误 • 采用新复极差法,查SSR表,自由度为12时 • 平均数大小排序、比较 1.43 4 8.17 2 = = = n Se SE e.多重比较 p 2 3 4 SSR0.05 3.08 3.23 3.33 SSR0.01 4.32 4.55 4.68 LSR0.05 4.40 4.62 4.76 LSR0.01 6.18 6.51 6.69 处理 苗高 显著性 0.05 0.01 D 29 a A B 23 b AB A 18 c BC C 14 c C f.结论 本试验中不同处理间有极显著差异(F值20.56>F.01值 (5.47)),其中在.05水平上D处理与其他处理有显著 差异,B处理与A、C处理有显著差异。 在.01水平D 处理与A、C处理间有显著差异,B处理与C处理有显 著差异。其他处理间差异均不显著。 1.组内观察值数目相等的单向分组资料的方差分析

第二节单向分组资料的方差分析 2、组内观察值数目不等的单向分组资料的方差分析 设有K个处理,每处理中的观察值数目分别为1, 029 ,k的资料,其数据类型如表: 1 2 3 21 20 24 其方差分析表为: 29 25 22 24 25 28 方差分析表 22 23 25 25 29 21 变异来源 自由度DF 平方和SS 均方MS F值 30 31 26 处理间 K-1 S2 S21 S2 24 ∑n(低-x) 26 26 误差 ∑n-k ∑∑x-x) Se2 20 21 总变异 ∑n-1 ∑x2-C
2、组内观察值数目不等的单向分组资料的方差分析 其方差分析表为: 方差分析表 变异来源 自由度DF 平方和SS 均方MS F值 处理间 K-1 St 2 St 2 / Se 2 误差 ∑ni -k Se 2 总变异 ∑ni -1 ∑x 2 -C − 2 ( ) i x x 2 n (x − x) i i 第二节 单向分组资料的方差分析 设有K个处理,每处理中的观察值数目分别为n1, n2 , ., nk的资料,其数据类型如表: 1 2 3 21 20 24 29 25 22 24 25 28 22 23 25 25 29 21 30 31 26 27 24 26 26 20 21

2、组内观察值数目不等的单向分组资料的方差分析 例:调查4种不同类型的水稻田28块,每田稻纵卷叶螟的百 丛虫口密度如表,问不同类型田的虫口密度有无差异? a.分解自由度 表4块稻田的虫口密度 2 3 4 总自由度=28-1=27 12 14 12 处理间自由度=k-1=3 13 10 2 11 处理内自由度=27一3=24 14 11 10 10 15 13 11 % b.计算平方和 15 14 12 8 C=3272÷28=3818.89 16 11 13 10 SST=∑x2-C 17 12 12 =4045-3818.89=226.11 11 SS=SS,=n∑(民-x2-∑/n-C T 102 73 80 72 T=327 102217+73216+802/8+7227-C 14.57 12.17 10.0 10.29x=11.68 =96.13 7 6 e 7 N=28 SSe=SST-SSt=129.98
例:调查4种不同类型的水稻田28块,每田稻纵卷叶螟的百 丛虫口密度如表,问不同类型田的虫口密度有无差异? 表 4块稻田的虫口密度 1 2 3 4 12 14 9 12 13 10 2 11 14 11 10 10 15 13 11 9 15 14 12 8 16 11 13 10 17 12 12 11 Ti 102 73 80 72 T=327 14.57 12.17 10.0 10.29 ni 7 6 8 7 N=28 i x x =11.68 a.分解自由度 总自由度=28-1=27 处理间自由度=k-1=3 处理内自由度=27-3=24 b.计算平方和 C=3272÷28=3 818.89 SST=∑x 2 -C =4 045-3 818.89=226.11 SSt= 1022 /7+732 /6+802 /8+722 /7-C =96.13 SSe=SST-SSt=129.98 SSt = n(xi − x) =Ti / n −C 2 2 2、组内观察值数目不等的单向分组资料的方差分析

2、组内观察值数目不等的单向分组资料的方差分析 C.计算均方 总均方 S2= SST =226.11÷15=40.13 nk -1 组间均方S? SS, =96.13÷3=32.04 k-1 组内均方S2= SS。 =129.98÷24=5.42 k(n-1)
C.计算均方 1 2 − = nk SS S T T 1 2 − = k SS S t t ( 1) 2 − = k n SS S e e =226.11÷15=40.13 组间均方 组内均方 总均方 =96.13÷3=32.04 =129.98÷24=5.42 2、组内观察值数目不等的单向分组资料的方差分析