C 首先建立>0电路的微分方程如下: de+e=cs+y,) t≥0 (10-7) d R 对应齐次微分方程的通解4c0为 uch(t)=Kes Ke RC 微分方程特解4c)的形式与电流源相同,为同一频率 的正弦时间函数,即 ucp(t)=Ucm cos(at+v)
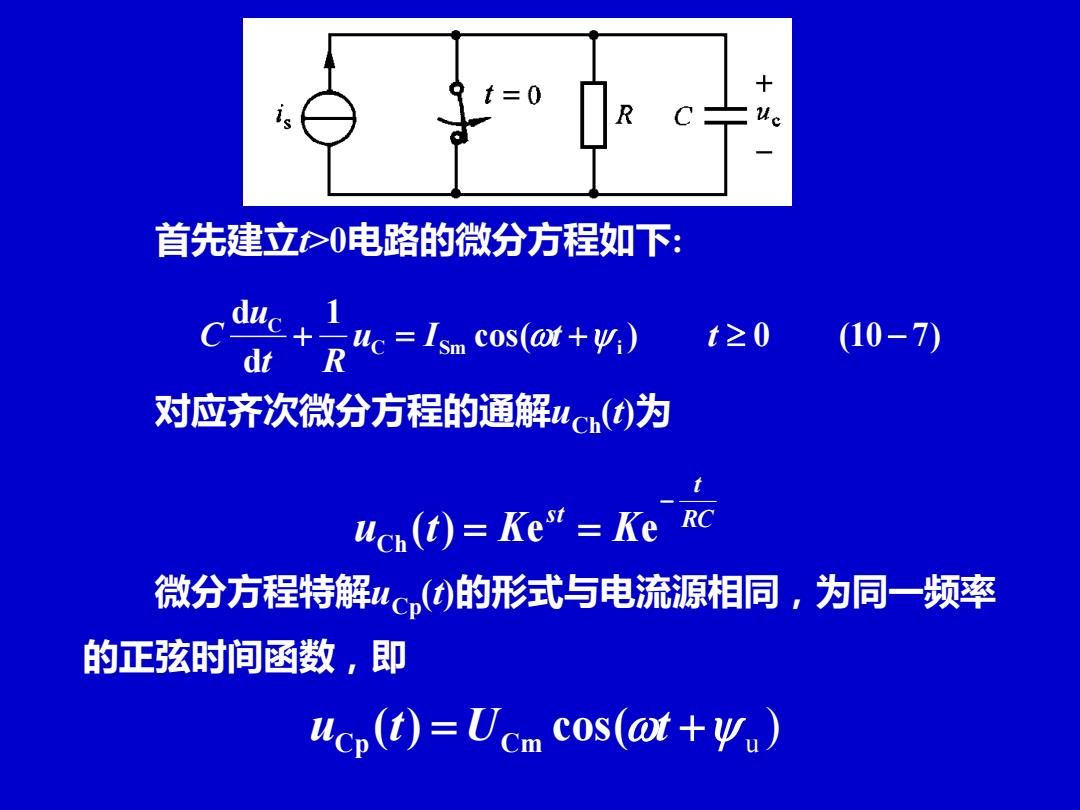
首先建立t>0电路的微分方程如下: cos( ) 0 (10 7) 1 d d C Sm i C + u = I t + t − t R u C 对应齐次微分方程的通解uCh(t)为 RC t st uCh (t) Ke Ke − = = 微分方程特解uCp(t)的形式与电流源相同,为同一频率 的正弦时间函数,即 ) = + u u (t) U cos( t Cp Cm

ucp(t)=Ucm cos(@t+) 为了确定U。和y,可以将上式代入微分方程中 c监+4e=人uma+y) t20 (10-7) -aCU.sin(w+g.)+Vocos(c+-y.)=人cod+y) 求解得到 Ucm=C+(/R) (10-8) V=Vi -arctan (@CR) (10-9)
为了确定UCm和ψu,可以将上式代入微分方程中 求解得到 arctan( ) (10 9) (10 8) (1/ ) u i 2 2 2 Sm Cm = − − − + = CR C R I U cos( ) 0 (10 7) 1 d d C Sm i C + u = I t + t − t R u C cos( ) ( ) 1 sin( ) − Cm + u + Cm + u = Sm + i U t I t R CU t cos ) = + u u (t) U cos( t Cp Cm

本电路的初始条件为零,属于零状态响应,所画出的 波形如图所示。曲线1表示通解,它是电路的自由响应,当 RC>0的条件下,它将随着时间的增加而按指数规律衰减到 零,称为暂态响应。曲线2表示特解,它按照正弦规律变化 其角频率与激励电源的角频率相同,当暂态响应衰减完后 它就是电路的全部响应,称为正弦稳态响应。 uc(t) Uemcos(@t+) 3 Ucmcosyu Uemcosve RC 图10-10
本电路的初始条件为零,属于零状态响应,所画出的 波形如图所示。曲线1表示通解,它是电路的自由响应,当 RC>0的条件下,它将随着时间的增加而按指数规律衰减到 零,称为暂态响应。曲线2表示特解,它按照正弦规律变化, 其角频率与激励电源的角频率相同,当暂态响应衰减完后, 它就是电路的全部响应,称为正弦稳态响应。 图 10-10

微分方程的完全解为 uc(t)=Ke RC+Ucm cos(@t+y) (t≥0) (10-10) 可以求得 K=uc(0)-Ucm cosVu 最后得到电容电压4c()的全响应为 uc(t)=[uc(0)-Ucm coswu]-e Rc +Ucm cos(ot+.)(t≥0) 暂态响应 正弦稳态响应 (10-11)
微分方程的完全解为 (10 10) ( ) e cos( ( 0) C C m − = + + − u t K U t t RC t ) u 可以求得 C Cm u K = u (0)−U cos 最后得到电容电压uC (t)的全响应为 (10 11) ( ) [ (0) cos ] e cos( ( 0) C C C m C m − = − + + − u t u U U t t RC t 暂态响应 正弦稳态响应 ) u u

二、 用相量法求微分方程的特解 求解正弦电流激励电路全响应的关键是求微分方程的特 解。假如能用相量来表示正弦电压电流,就可以将常系数 微分方程转变为复系数的代数方程,便于使用各种计算工 具。现将这种相量法介绍如下: is(t)=Ism cos(@t+i)=Re(ismei@) ucp(t)=Ucm cos(@t+)=ReUcmeia) 代入微分方程 CRe)-Rec)
二、 用相量法求微分方程的特解 ( ) cos( ) Re( e ) ( ) cos( ) Re( e ) j C p C m C m j S Sm Sm t t u t U t U i t I t I = + = = + = u i 求解正弦电流激励电路全响应的关键是求微分方程的特 解。假如能用相量来表示正弦电压电流,就可以将常系数 微分方程转变为复系数的代数方程,便于使用各种计算工 具。现将这种相量法介绍如下: 代入微分方程 Re( e ) Re( e ) R 1 [Re( e )] d d j Sm j Cm j Cm t t t U U I t C + =