
2.2热力学第一定律 2.2.1热 由于温度差引起的能量从环境向系统的流动 称为热(heat),以符号Q表示,它的SI单位为:J。 Q值符号的规定: •系统吸热,Q〉0 系统放热,Q〈0 Q不是状态函数,Q的数值与具体途径有关
2.2 热力学第一定律 2.2.1 热 由于温度差引起的能量从环境向系统的流动 称为热(heat),以符号Q表示,它的SI单位为:J。 Q值符号的规定: •系统吸热,Q 〉0 •系统放热,Q〈0 Q不是状态函数, Q的数值与具体途径有关
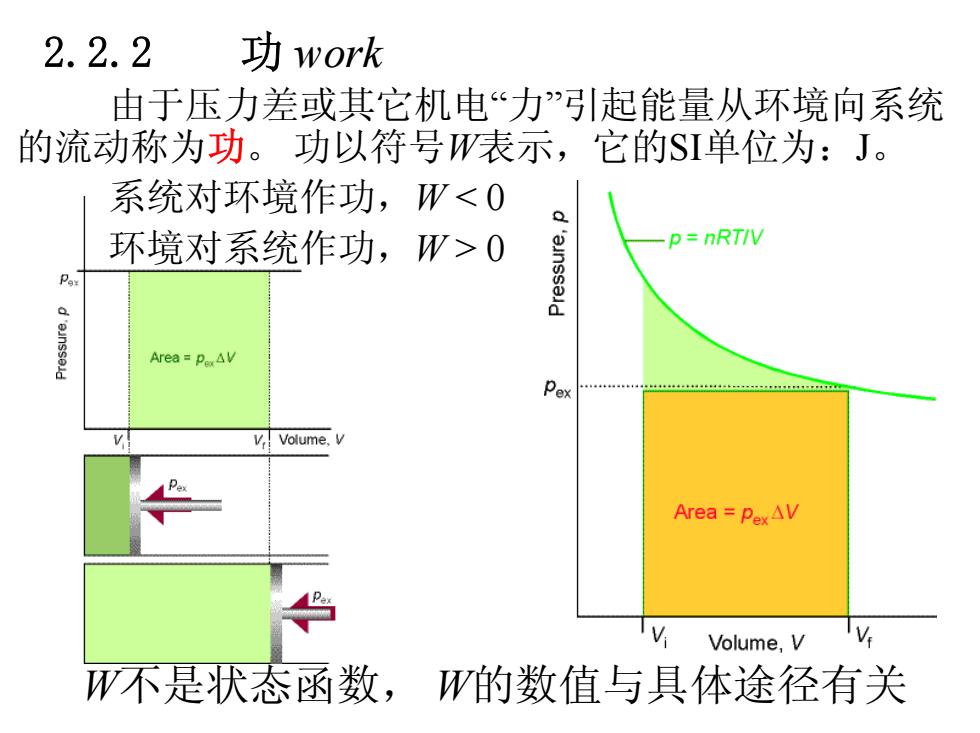
2.2.2 功work 由于压力差或其它机电“力”引起能量从环境向系统 的流动称为功。功以符号W表示,它的S单位为:J。 系统对环境作功,W<0 环境对系统作功,W>0 p=nRTIV Pax Area=peAV Pex V Volume,V Area=PexAV Volume,V W不是状态函数,W的数值与具体途径有关
2.2.2 功 work 由于压力差或其它机电“力”引起能量从环境向系统 的流动称为功。 功以符号W表示,它的SI单位为:J。 系统对环境作功,W < 0 环境对系统作功,W > 0 W不是状态函数, W的数值与具体途径有关
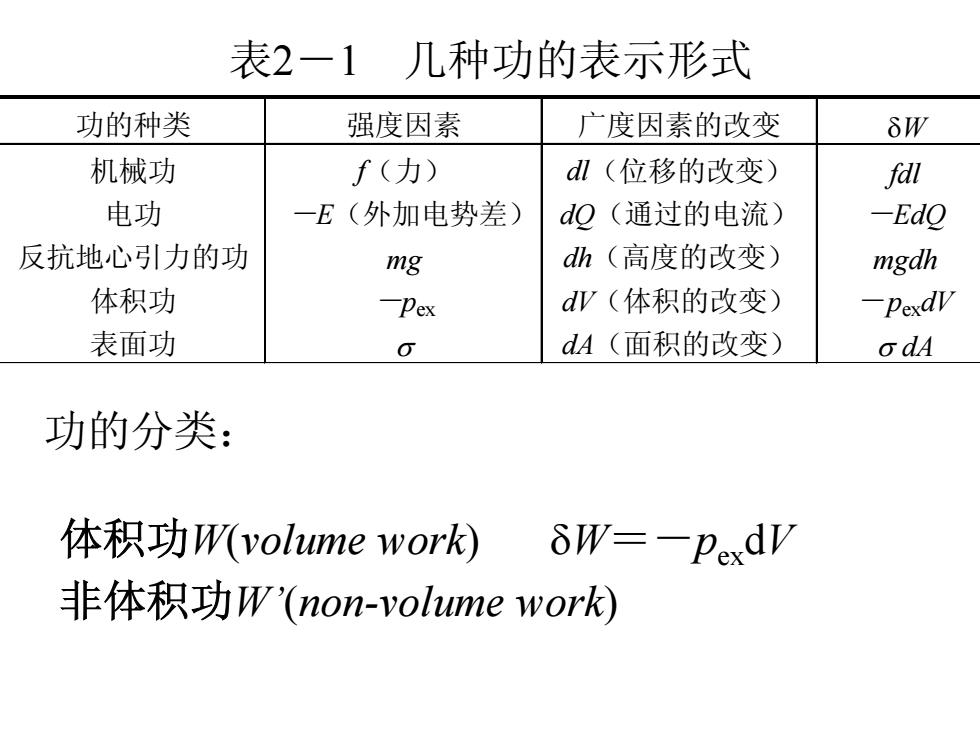
表2一1几种功的表示形式 功的种类 强度因素 广度因素的改变 δW 机械功 f(力) dl(位移的改变) 电功 一E(外加电势差) dQ(通过的电流) -Edo 反抗地心引力的功 mg dh(高度的改变) mgdh 体积功 Pex dV(体积的改变) Pexdv 表面功 dA(面积的改变) odA 功的分类: 体积功W(volume work) δW=-Pexdv 非体积功W'(non-volume work)
表2-1 几种功的表示形式 功的种类 强度因素 广度因素的改变 δW 机械功 f(力) dl(位移的改变) fdl 电功 -E(外加电势差) dQ(通过的电流) -EdQ 反抗地心引力的功 mg dh(高度的改变) mgdh 体积功 -pex dV(体积的改变) -pexdV 表面功 σ dA(面积的改变) σ dA 功的分类: 体积功W(volume work) δW=-pexdV 非体积功W’(non-volume work)

2.2.3 热力学能thermodynamic energy 热力学能(thermodynamic energy)以前 称为内能(internal energy),它是指系统内部 能量的总和,包括分子运动的平动能、分子 内的转动能、振动能、电子能、核能以及各 种粒子之间的相互作用位能等。 热力学能UU的SI单位为:J。 U是状态函数,△U的数值只与系统的始、终 态,而与具体途径有关。 热力学能U是系统的广度性质
2.2.3 热力学能thermodynamic energy 热力学能(thermodynamic energy)以前 称为内能(internal energy),它是指系统内部 能量的总和,包括分子运动的平动能、分子 内的转动能、振动能、电子能、核能以及各 种粒子之间的相互作用位能等。 热力学能U的SI单位为:J。 U是状态函数,△U的数值只与系统的始、终 态,而与具体途径有关。 热力学能U是系统的广度性质

2.2.4 热力学第一定律 焦耳(Joule)和迈耶(Mayer)自1840年起,历经20多 年,用各种实验求证热和功的转换关系,得到的结果是 一致的。 即:1cal=4.1840J 这就是著名的热功当量,为能量守恒原理提供了 科学的实验证明。 到1850年,科学界公认能量守恒定律是自然界的 普遍规律之一。能量守恒与转化定律可表述为: 自然界的一切物质都具有能量,能量有各种不同 形式,能够从一种形式转化为另一种形式,但在转化 过程中,能量的总值不变
2.2.4 热力学第一定律 焦耳(Joule)和迈耶(Mayer)自1840年起,历经20多 年,用各种实验求证热和功的转换关系,得到的结果是 一致的。 即: 1 cal = 4.1840 J 这就是著名的热功当量,为能量守恒原理提供了 科学的实验证明。 到1850年,科学界公认能量守恒定律是自然界的 普遍规律之一。能量守恒与转化定律可表述为: 自然界的一切物质都具有能量,能量有各种不同 形式,能够从一种形式转化为另一种形式,但在转化 过程中,能量的总值不变