
课程类别:通识公共必修课 学分:3学分 学 时:48学时 一、课程简介 本课程是高等学校农科类本科各专业必修的重要基础课,是培养学生掌握科学思维能 力、掌握数学知识和数学技能的重要基础课程。课程系统介绍行列式、矩阵的基本运算、向 量组线性相关性的理论、线性方程组的解的理论和求解方法:概率论的基本概念、事件概率 的多种求法、随机变量及其分布的理论以及随机变量的数字特征的求值方法。课程所论及的 科学思想和方法论,在社会各领域中具有广泛应用和强劲的活力,课程安排在第一学期开设, 是考虑到农科学生必须具备高等数学的基础知识,才能理解掌握用数学语言表述的数学规 律,并学会用数学的方法解决问恩,为专业基础课打下良好的基础。课程教学的主要任务 是培养学生掌握经典数学和近代数学的基本概念、基本原理及基本方法,掌握当代数学技术 的基本技能:培养学生学会建立数学模型,具备用数学方法解释自然规律、探索自然界奥秘 的科学思维能力。 二、教学目标 (一)总体目标 本课程是高等学校农科类本科各专业必修的重要基础课。通过本课程的学习,使学生对 线性代数、概率论的基本概念、基本理论、基本方法有比较系统的认识,构建较为宽广的知 识结构。逐步培养学生抽象概括问题的能力、 一定的逻辑推理能力、比较熟练地运 能力天 自学能力,提高学生在数学方面的素质和修养,培养学生综合运用所学知识分析问题、解决 问题的能力,学会运用本课程提供的数学思想、数学方法解决简单的应用问题,激发学生探 索与创新意识,为学习其它后续基出课程打下基础。 (二)课程目标 本课程的牧学目标是帮助学生正确理解和掌握线性代数、概率论的基本概念、基本理论 熟练掌握线性代数、概率论中的基本方法和基本演算能力,培养学生思维能力和推理能力, 熟练、精确地运算能力,从而为进一步学习其他课程打下必要基础 课程目标1:通过教师的言传身教,学生能积极践行社会主义核心价值观,体会线性代 数、概率论的数学思想方法,理解线性代数、概率论的数学思想,形成无限与有限相统一的 辩证唯物主义观点,完善认识世界的方法:学生通过学习本课程的发展历程,了解到数学文 化的多样性与马克思主义哲学观对现代数学发展的重要意义,通过知识的融合与深化,使学 生增强学以致用的能力与意识。 课程目标2:通过本课程的学习,使学生对线性代数、概率论的基本概念、基本理论、 基本方法有比较系统的认识,构建较为宽广的知识结构。 课程目标3:通过本课程的学习,逐步培养学生抽象概括问题的能力、一定的逻辑推理 能力、比较熟练的运算能力和自学能力,提高学生在数学方面的素质和修养,培养学生综合 运用所学知识分析问题、解决问题的能力: 课程目标4:通过本课程的学习,使学生学会运用本课程提供的数学思想、数学方法解
13 课程类别:通识公共必修课 学 分:3 学分 学 时:48 学时 一、课程简介 本课程是高等学校农科类本科各专业必修的重要基础课,是培养学生掌握科学思维能 力、掌握数学知识和数学技能的重要基础课程。课程系统介绍行列式、矩阵的基本运算、向 量组线性相关性的理论、线性方程组的解的理论和求解方法;概率论的基本概念、事件概率 的多种求法、随机变量及其分布的理论以及随机变量的数字特征的求值方法。课程所论及的 科学思想和方法论,在社会各领域中具有广泛应用和强劲的活力。课程安排在第一学期开设, 是考虑到农科学生必须具备高等数学的基础知识,才能理解掌握用数学语言表述的数学规 律,并学会用数学的方法解决问题,为专业基础课打下良好的基础。 课程教学的主要任务 是培养学生掌握经典数学和近代数学的基本概念、基本原理及基本方法,掌握当代数学技术 的基本技能;培养学生学会建立数学模型,具备用数学方法解释自然规律、探索自然界奥秘 的科学思维能力。 二、教学目标 (一)总体目标 本课程是高等学校农科类本科各专业必修的重要基础课。通过本课程的学习,使学生对 线性代数、概率论的基本概念、基本理论、基本方法有比较系统的认识,构建较为宽广的知 识结构。逐步培养学生抽象概括问题的能力、一定的逻辑推理能力、比较熟练地运算能力和 自学能力,提高学生在数学方面的素质和修养,培养学生综合运用所学知识分析问题、解决 问题的能力,学会运用本课程提供的数学思想、数学方法解决简单的应用问题,激发学生探 索与创新意识,为学习其它后续基础课程打下基础。 (二)课程目标 本课程的教学目标是帮助学生正确理解和掌握线性代数、概率论的基本概念、基本理论, 熟练掌握线性代数、概率论中的基本方法和基本演算能力,培养学生思维能力和推理能力, 熟练、精确地运算能力,从而为进一步学习其他课程打下必要基础。 课程目标 1:通过教师的言传身教,学生能积极践行社会主义核心价值观,体会线性代 数、概率论的数学思想方法,理解线性代数、概率论的数学思想,形成无限与有限相统一的 辩证唯物主义观点,完善认识世界的方法;学生通过学习本课程的发展历程,了解到数学文 化的多样性与马克思主义哲学观对现代数学发展的重要意义,通过知识的融合与深化,使学 生增强学以致用的能力与意识。 课程目标 2:通过本课程的学习,使学生对线性代数、概率论的基本概念、基本理论、 基本方法有比较系统的认识,构建较为宽广的知识结构。 课程目标 3:通过本课程的学习,逐步培养学生抽象概括问题的能力、一定的逻辑推理 能力、比较熟练的运算能力和自学能力,提高学生在数学方面的素质和修养,培养学生综合 运用所学知识分析问题、解决问题的能力。 课程目标 4:通过本课程的学习,使学生学会运用本课程提供的数学思想、数学方法解
决简单的应用问题,激发学生的探索与创新意识,为学习其它基础课程和专业课程打下基础。 三、教学内容和学时分配 表1课程教学安排表 讲实实上 章节/单元 主要教学内容 课验 时时学 学 主要敦学方法 数数时时 1 行列式 6 课堂讲授 2 矩阵及其运算 课堂讲授 向量及线性方程组 10 课堂讲授 随机事件与概率 8 课堂讲投 5 随机变量及其分布 10 课堂讲授 6 随机变量的数字特征 6 课堂讲授 合计 48 第一音行列式 教学要求:了解行列式的概念,掌握行列式的性质及用行列式的性质和行列式按行(列) 展开定理计算行列式。 教学内容:(1)行列式的定义 (2)行列式的性质 (3)行列式的展开定理 (4)n阶行列式的计算 (5)克莱姆法则 (6)当mm时,线性齐次方程组有非零解的条件 重点难点:重点:行列式的性质,行列式按行(列)展开,克莱姆法则。 难点:行列式的性质,行列式按行(列)展开 思政元素:通过方程的演变过程介绍多项式代数和线性代数在数学中的地位,让学生了 解数系 及代数学发展的历史、体会由特殊到一般的数学思维的方法和魅力,引发学生学习数学和解 决问题的兴趣。 第十四章矩阵及其运算 教学要求:理解矩阵、逆矩阵、矩阵的秩的概念:了解矩阵初等变换、初等矩阵的性质、 矩阵等价的概念,了解分块矩阵及其运算:掌握矩阵的运算、逆矩阵的性质、矩阵可逆的充 分必要条件,掌握用初等变换求矩阵的秩和逆矩阵的方法。 教学内容:(1)矩阵概念 (2)矩阵的加法,数与矩阵相乘,矩阵与矩阵相乘
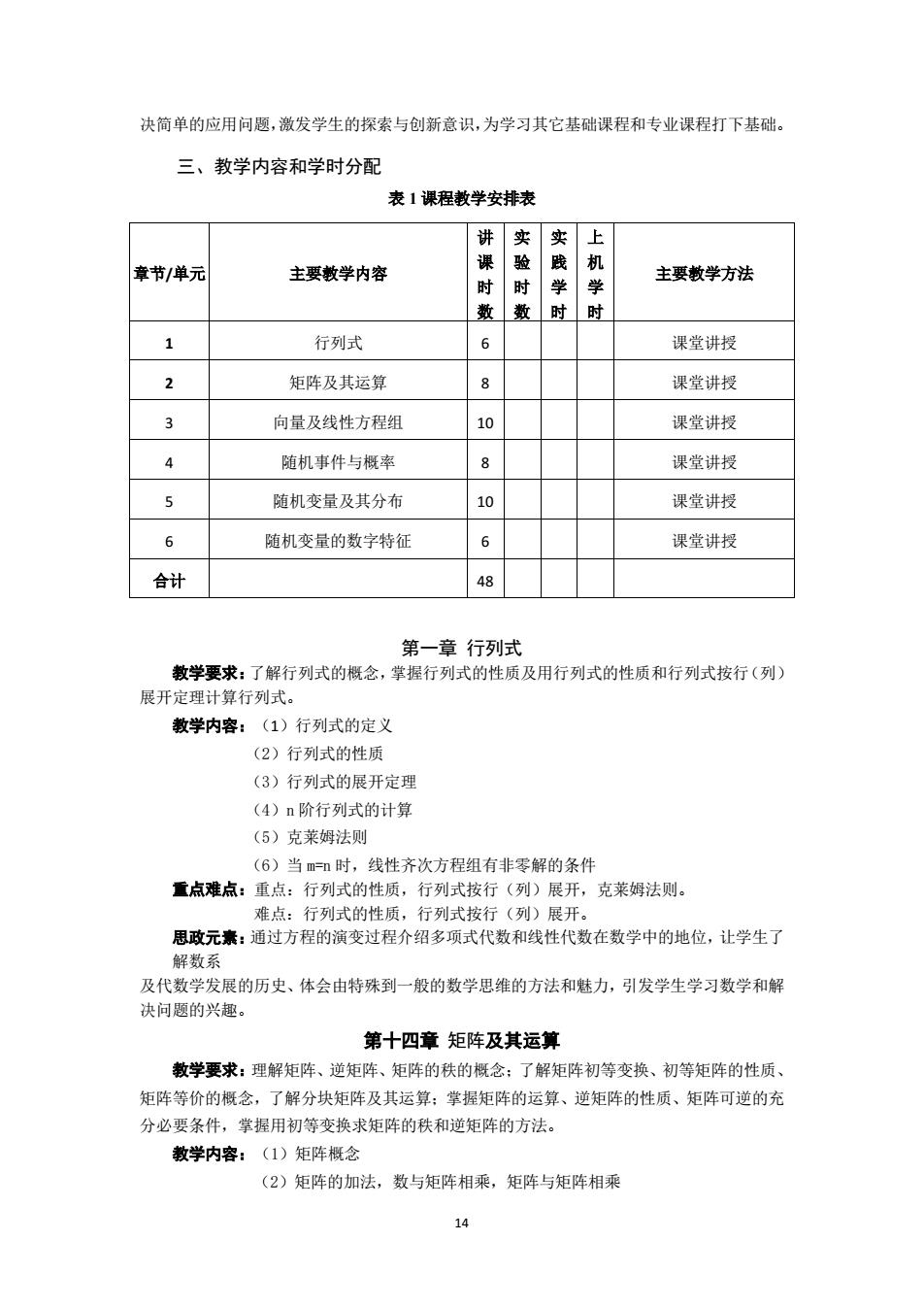
14 决简单的应用问题,激发学生的探索与创新意识,为学习其它基础课程和专业课程打下基础。 三、教学内容和学时分配 表 1 课程教学安排表 章节/单元 主要教学内容 讲 课 时 数 实 验 时 数 实 践 学 时 上 机 学 时 主要教学方法 1 行列式 6 课堂讲授 2 矩阵及其运算 8 课堂讲授 3 向量及线性方程组 10 课堂讲授 4 随机事件与概率 8 课堂讲授 5 随机变量及其分布 10 课堂讲授 6 随机变量的数字特征 6 课堂讲授 合计 48 第一章 行列式 教学要求:了解行列式的概念,掌握行列式的性质及用行列式的性质和行列式按行(列) 展开定理计算行列式。 教学内容:(1)行列式的定义 (2)行列式的性质 (3)行列式的展开定理 (4)n 阶行列式的计算 (5)克莱姆法则 (6)当 m=n 时,线性齐次方程组有非零解的条件 重点难点:重点:行列式的性质,行列式按行(列)展开,克莱姆法则。 难点:行列式的性质,行列式按行(列)展开。 思政元素:通过方程的演变过程介绍多项式代数和线性代数在数学中的地位,让学生了 解数系 及代数学发展的历史、体会由特殊到一般的数学思维的方法和魅力,引发学生学习数学和解 决问题的兴趣。 第十四章 矩阵及其运算 教学要求:理解矩阵、逆矩阵、矩阵的秩的概念;了解矩阵初等变换、初等矩阵的性质、 矩阵等价的概念,了解分块矩阵及其运算;掌握矩阵的运算、逆矩阵的性质、矩阵可逆的充 分必要条件,掌握用初等变换求矩阵的秩和逆矩阵的方法。 教学内容:(1)矩阵概念 (2)矩阵的加法,数与矩阵相乘,矩阵与矩阵相乘

(3)矩阵的转置、方阵的行列式、方阵的幂、共轭矩阵 (4)几种特殊类型的矩阵 (5)逆阵的定义、求法及可逆方阵的充要条件 (6)矩阵的分块 (7)矩阵的初等变换与初等矩 (8)矩阵的秩 重点难点:重点:矩阵的运算,逆阵,矩阵分块法。 难点:矩阵的运算,逆吟 课程思政:通过讲解矩阵的应用,让学生体会到数学工具的重要性:通过讲解各种特殊 形状的 矩阵到分块矩阵,从矩阵的初等变换到分块初等变换,让学生能从数学的角度充分领会世界 的多样性、可比性和类似性:通过证明或反例讨论矩阵运算律,培养学生反思精神和严谨的 思维 第十五章向量及线性方程组 教学要求:理解维向量、向量的线性组合与线性表示、向量组线性相关、线性无关的 概念:掌握向量组线性相关、线性无关的有关性质及判别法:了解向量组的极大线性无关组 和向量组的秩的概念,会求向量组的极大线性无关组及秩。理解齐次线性方程组有非零解的 充分必要条件及非齐次线性方程组有解的充分必要条件,理解齐次线性方程组的基础解系及 通解的概念:掌据齐次线性方程组的基础解系和通解的求法,会用初等行变换求解非线性方 程组。 教学内容:(1)行列式的定义 (2)线性相关与线性无关 (3)向量组的等价 (4)线性相关性的判别定理 (5)矩阵的秩与向量组的秩 (6)最大线性无关向量组 (7)齐次线性方程组解向量及性质,基础解系 (8)求解齐次线性方程组 (9)非齐次线性方程组解向量的性质及解的结构 (10)求解非齐次线性方程组 重点难点:重点:维向量,线性相关与线性无关,向量组的秩。方程组的解向量的性 质,基 础解系,方程组的求解方法。 难点:线性相关与线性无关,向量组的秩,基础解系,方程组的求解方法。 课程思政:通过案列归钠以及分离系数讲解一般线性方程组的解的情形和解法,让学生 体会到 透过现象看本质的数学思考方法:通过讲解向量组线性相关和线性无关,让学生能从数学的 角度充分领会世界的多样性和复杂性:通过讲解齐次线性方程组基础解系和线性方程组解的 结构,让学生体会用有限表示无限的辩证唯物主义观点。培养学生提出问题、分析问题、解 决问题的能力
15 (3)矩阵的转置、方阵的行列式、方阵的幂、共轭矩阵 (4)几种特殊类型的矩阵 (5)逆阵的定义、求法及可逆方阵的充要条件 (6)矩阵的分块 (7)矩阵的初等变换与初等矩阵 (8)矩阵的秩 重点难点:重点:矩阵的运算,逆阵,矩阵分块法。 难点:矩阵的运算,逆阵。 课程思政:通过讲解矩阵的应用,让学生体会到数学工具的重要性;通过讲解各种特殊 形状的 矩阵到分块矩阵,从矩阵的初等变换到分块初等变换,让学生能从数学的角度充分领会世界 的多样性、可比性和类似性;通过证明或反例讨论矩阵运算律,培养学生反思精神和严谨的 思维。 第十五章 向量及线性方程组 教学要求:理解 n 维向量、向量的线性组合与线性表示、向量组线性相关、线性无关的 概念;掌握向量组线性相关、线性无关的有关性质及判别法;了解向量组的极大线性无关组 和向量组的秩的概念,会求向量组的极大线性无关组及秩。理解齐次线性方程组有非零解的 充分必要条件及非齐次线性方程组有解的充分必要条件,理解齐次线性方程组的基础解系及 通解的概念;掌握齐次线性方程组的基础解系和通解的求法,会用初等行变换求解非线性方 程组。 教学内容:(1)行列式的定义 (2)线性相关与线性无关 (3)向量组的等价 (4)线性相关性的判别定理 (5)矩阵的秩与向量组的秩 (6)最大线性无关向量组 (7)齐次线性方程组解向量及性质,基础解系 (8)求解齐次线性方程组 (9)非齐次线性方程组解向量的性质及解的结构 (10)求解非齐次线性方程组 重点难点:重点:n 维向量,线性相关与线性无关,向量组的秩。方程组的解向量的性 质,基 础解系,方程组的求解方法。 难点:线性相关与线性无关,向量组的秩,基础解系,方程组的求解方法。 课程思政:通过案列归纳以及分离系数讲解一般线性方程组的解的情形和解法,让学生 体会到 透过现象看本质的数学思考方法;通过讲解向量组线性相关和线性无关,让学生能从数学的 角度充分领会世界的多样性和复杂性;通过讲解齐次线性方程组基础解系和线性方程组解的 结构,让学生体会用有限表示无限的辩证唯物主义观点。培养学生提出问题、分析问题、解 决问题的能力

第十六章随机事件与概率 教学要求:理解随机事件和样木空间的概念:熟练掌握事件之间的关系与基本运算。理 解事件频率的概念:了解随机现象的统计规律性。理解古典概率的概念:掌握概率的基本性 质:理解条件概率的概念:掌握乘法定理、全概率公式和贝叶斯公式:理解事件独立性的概 念:会应用事件的独立性进行概率计算。 教学内容:(1)随机试验与随机事件 (2)事件之间的关系与及运算 (3)概率的续计定义 (4)古典概型 (5)概率的一般定义 (6)概率的性质 (7)条件概率与事件的独立性 (8)独立试验序列揽型 (9)全概率公式与贝叶斯(Bayes)公式 重点难点:重点:随机事件,概率,条件概率与独立性,全概率公式与贝叶斯(Bayes) 公式。 难点:条件概率与独立性,全概率公式与贝叶斯(Baes)公式。 课程思政:通过对概率的公理化定义和相关公式学习,让学生体会到概率思维的魅力 引发学生借助概率语言描述和解决问题的兴趣。 第十七章随机变量及其分布 教学要求:了解随机变量的概念:理解分布函数的概念和性质:掌握离散型随机变量和 连续型 随机变量的描述方法:理解分布律与分布密度的概念和性质。掌提二项分布、泊松分布、均 匀分布、 指 分布和正态分布:会利用概率分布计算有关事件的概率。 教学内容:(1)随机变量的概念 (2)离散型随机变量及其概率分布 (3)几种常见的离散分布 (4)贿机变量的分布函数的定义及性质 (5)连续型随机变量及其概率密度 (6)几种常见的连续型随机变量的分布 (7)随机变量的函数的分布 重点难点:重点:随机变量及其分布,随机变量函数的分布,几种重要的离散型、连续 型分布。 难点:随机变量的函数的分有 课程思政:通过对分布函数,分布律和密度函数的学习,让学生学会运用不同的方式刻画 随机性, 让学生体会到事物是普遍联系的。 第十八章随机变量的数字特征 教学要求:理解数学期望、方差的概念,掌握它们的性质与计算:会计算随机变量函 数的数学期望:熟记二项分布、泊松分布、均匀分布、指数分布和正态分布的数学期望与方 差。 教学内容:(1)数学期望的定义及性质 16
16 第十六章 随机事件与概率 教学要求:理解随机事件和样本空间的概念;熟练掌握事件之间的关系与基本运算。理 解事件频率的概念;了解随机现象的统计规律性。理解古典概率的概念;掌握概率的基本性 质;理解条件概率的概念;掌握乘法定理、全概率公式和贝叶斯公式;理解事件独立性的概 念;会应用事件的独立性进行概率计算。 教学内容:(1)随机试验与随机事件 (2)事件之间的关系与及运算 (3)概率的统计定义 (4)古典概型 (5)概率的一般定义 (6)概率的性质 (7)条件概率与事件的独立性 (8)独立试验序列模型 (9)全概率公式与贝叶斯(Bayes)公式 重点难点:重点:随机事件,概率,条件概率与独立性,全概率公式与贝叶斯(Bayes) 公式 。 难点:条件概率与独立性,全概率公式与贝叶斯(Bayes)公式。 课程思政:通过对概率的公理化定义和相关公式学习,让学生体会到概率思维的魅力, 引发学生借助概率语言描述和解决问题的兴趣。 第十七章 随机变量及其分布 教学要求:了解随机变量的概念;理解分布函数的概念和性质;掌握离散型随机变量和 连续型 随机变量的描述方法;理解分布律与分布密度的概念和性质。掌握二项分布、泊松分布、均 匀分布、指数分布和正态分布;会利用概率分布计算有关事件的概率。 教学内容:(1)随机变量的概念 (2)离散型随机变量及其概率分布 (3)几种常见的离散分布 (4)随机变量的分布函数的定义及性质 (5)连续型随机变量及其概率密度 (6)几种常见的连续型随机变量的分布 (7)随机变量的函数的分布 重点难点:重点:随机变量及其分布,随机变量函数的分布,几种重要的离散型、连续 型分布。 难点:随机变量的函数的分布。 课程思政:通过对分布函数,分布律和密度函数的学习,让学生学会运用不同的方式刻画 随机性, 让学生体会到事物是普遍联系的。 第十八章 随机变量的数字特征 教学要求:理解数学期望、方差的概念,掌握它们的性质与计算;会计算随机变量函 数的数学期望;熟记二项分布、泊松分布、均匀分布、指数分布和正态分布的数学期望与方 差。 教学内容:(1)数学期望的定义及性质
(2)随机变量函数的数学期望 (3)方若的定义及性质 :4)几种常见的随机变量的期望与方差 重点难点:重点:数学期望、方差的概念,常见分布的期望和方差。 难点:二项分布、泊松分布、正态分布的期望和方差。 课程思政:通过对数学期望,方差等数字特征的学习,让学生知道可以通过不同的方式 来阿随机变最,从而可以拓展学生变换思维。 四、教学方法 讲授法:本课程是高等学校农科类本科各专业的一门必修的重要基础课。在课程教学中 以启发式课堂讲授为主,结合各种教学方 有意识地增 7训练、 启发思维、 培 养能力, 过借助现代化教学工具和教学手段,逐步培养和提高学生的抽象、推理、归纳能力,研究问 题、解决问题的能力,自我获取知识的能力,强化学生创新创业能力的培养,使学生在今后 的学习和工作中能通过自学、分析、研究得以提高。 五、课程考核与成绩评定 考核方式:本课程考试均采取闭卷考试形式(包括期中考试与期末考试) 成绩评定:本课程采用百分制评定学习,记分方法如下:平时成绩(包括期中考试、 上课出勒、平时作业等)占30%,期末考试成绩占70%。 表2课程考核内容、考核形式及支排课程目标 成绩分项考核/评价环节 建议 百分比 考核/评价细则 备注 出勤、作业 上课出勒、平时作业等 课程目标1 平时成绩 期中考试 20 闭卷期中考试 课程目标2-3 期末成绩期末考试 70 闭卷期末考试 课程目标1-4 小计 100 六、课程教学资源 选用教材: 《线性代数(第4版)》,陈建华编著,机械工业出版社,2022年1月第9次印刷. 《概率论与数理统计(第4版)》,宗序平编著,机械工业出版社,2021年6月第5次 印刷 选读书目 [1]《线性代数》(第7版),同济大学数学系编,高等教育出版社,2019: 「2]《线性代数》(第3版),张良云主绵,高等教有出版社,2010: [3]《概率论与数理统计》(第5版),盛骤谢式千潘承毅主编,高等教有出版,2020: 「41《应用概率统计》,张国权刘金山主编。中国农业出版社,2015: 5]ntroductionto Linear,Wellesley-Cambridge Press,016 [6](Elementary Probability Theory:With Stochastic Processes and an Introduction to Mathematical Finance》,钟开菜,世界图书出版公司,2010. 学习网站:扬州大学网络教学平台(eol,y2u.edu.cnl. 17
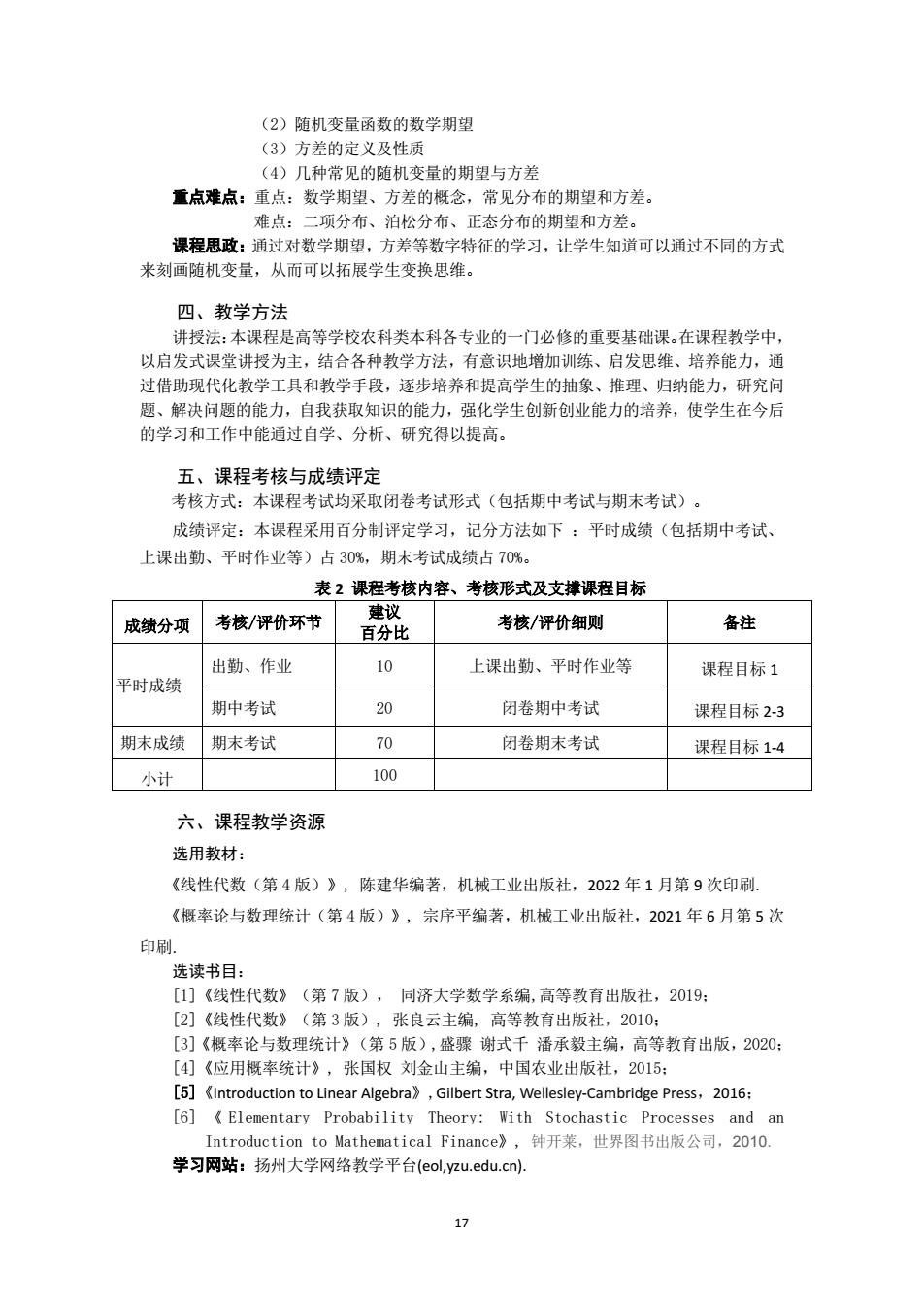
17 (2)随机变量函数的数学期望 (3)方差的定义及性质 (4)几种常见的随机变量的期望与方差 重点难点:重点:数学期望、方差的概念,常见分布的期望和方差。 难点:二项分布、泊松分布、正态分布的期望和方差。 课程思政:通过对数学期望,方差等数字特征的学习,让学生知道可以通过不同的方式 来刻画随机变量,从而可以拓展学生变换思维。 四、教学方法 讲授法:本课程是高等学校农科类本科各专业的一门必修的重要基础课。在课程教学中, 以启发式课堂讲授为主,结合各种教学方法,有意识地增加训练、启发思维、培养能力,通 过借助现代化教学工具和教学手段,逐步培养和提高学生的抽象、推理、归纳能力,研究问 题、解决问题的能力,自我获取知识的能力,强化学生创新创业能力的培养,使学生在今后 的学习和工作中能通过自学、分析、研究得以提高。 五、课程考核与成绩评定 考核方式:本课程考试均采取闭卷考试形式(包括期中考试与期末考试)。 成绩评定:本课程采用百分制评定学习,记分方法如下 :平时成绩(包括期中考试、 上课出勤、平时作业等)占 30%,期末考试成绩占 70%。 表 2 课程考核内容、考核形式及支撑课程目标 成绩分项 考核/评价环节 建议 百分比 考核/评价细则 备注 平时成绩 出勤、作业 10 上课出勤、平时作业等 课程目标 1 期中考试 20 闭卷期中考试 课程目标 2-3 期末成绩 期末考试 70 闭卷期末考试 课程目标 1-4 小计 100 六、课程教学资源 选用教材: 《线性代数(第 4 版)》, 陈建华编著,机械工业出版社,2022 年 1 月第 9 次印刷. 《概率论与数理统计(第 4 版)》, 宗序平编著,机械工业出版社,2021 年 6 月第 5 次 印刷. 选读书目: [1]《线性代数》(第 7 版), 同济大学数学系编,高等教育出版社,2019; [2]《线性代数》(第 3 版), 张良云主编, 高等教育出版社,2010; [3]《概率论与数理统计》(第 5 版),盛骤 谢式千 潘承毅主编,高等教育出版,2020; [4]《应用概率统计》, 张国权 刘金山主编,中国农业出版社,2015; [5]《Introduction to Linear Algebra》,Gilbert Stra, Wellesley-Cambridge Press,2016; [6] 《 Elementary Probability Theory: With Stochastic Processes and an Introduction to Mathematical Finance》, 钟开莱,世界图书出版公司,2010. 学习网站:扬州大学网络教学平台(eol,yzu.edu.cn)