
2021-12-28 《数学建模》课件汇总 大型飞 O 机内舱 。4 m4 第26页,共105页
2021-12-28 4 19 大型飞 机内舱 《数学建模》课件汇总 第26页,共105页

2021-12-28 《数学建模》课件汇总 3.3问题分析 对问题进行充分的前期分析以前过早着手决问题往往会 陷入一些意想不到的陷阱,或者偏高解决问题的方向, 问愿的前期分析包括: 明确问愿、分析条件、分析数据 一明确问题 为什么间愿前期分析至关重要? 例331一家大商业印刷公司的经理就关于应该多少推销 数学建模问愿往往含混不清,可能的原因有: 员的问题征询你的意见 *提出问愿的人未能清楚地表述问愿。 通到一个新问愿时,首先应问自己 *不同领城的人交流出现故障 “究竟需要做什么?” ·各领域的应用者提出问愿时,未给出恰当的条件, 为明确问题,可向有关人员询问如下问题: 1.公司的规棋有多大? ·未能准确理解问题 2.该公司的推销员的工作方式? 海e0行 锦行王 着最点是对各类推销队伍的工作效果进行分析 二条件及数据分析 原问愿“推销员人数问愿”明确为: 设置好问愿的目标态,着手工作还需要做以下工作: (1)不同规模的幣售队伍会有什么影响: (2)怎样从他们的销售工作中获取最大的收益. 1.收集必要的资料和数据; 明确了工作的目标,即设置好问愿的目标态 2分析现有的数据和 条件,使问题进一步明 确化。 例(96竟妻B)节水洗衣机问愿 例(96竞妻B)节水洗农机问愿 怎样收集数据和资料? 可在各类图书馆、网上查阅、向专家询问、通过试验来 分析:愿目中设有一个数据,但问题却需要比较多的数据及 得到 条件,如 收集数据应列入工作计划,并注意: *衣服的洗净效果指标(包括污物和残留洗涤剂): 1。向有关人员调查情况应事先设计好问愿: 2. *不同质地衣物的脱水事或衣物的含水量C: 事先确定所需资料清单、资料来源、收集方式。 有条理的收集计划可以为后期的工作 *洗衣机的最高水位H、最低水位L: 创造良好的条件 *各类污物(泥土、油腻等)和洗涤剂在水中的溶解特性等。 对收集到的或者现有的资料和数据要做仔细分析,使问题 进一步明确。 等。用 第27页,共105页 1
2021-12-28 1 电子科技大学 1 问题的前期分析 包括: 明确问题、分析条件、分析数据 为什么问题前期分析至关重要? 数学建模问题往往含混不清,可能的原因有: * 提出问题的人未能清楚地表述问题 . * 不同领域的人交流出现故障. * 各领域的应用者提出问题时,未给出恰当的条件. * 未能准确理解问题. 电子科技大学 2 对问题进行充分的前期分析以前,过早着手决问题,往往会 陷入一些意想不到的陷阱,或者偏离解决问题的方向. 一. 明确问题 例3.3.1 一家大商业印刷公司的经理就关于应该雇多少推销 员的问题征询你的意见. “究竟需要做什么?” 为明确问题 ,可向有关人员询问如下问题: 1. 公司的规模有多大? 2. 该公司的推销员的工作方式? 遇到一个新问题时,首先应问自己 电子科技大学 3 着眼点是对各类推销队伍的工作效果进行分析 原问题“推销员人数问题” 明确为: (1)不同规模的销售队伍会有什么影响; (2)怎样从他们的销售工作中获取最大的收益. 明确了工作的目标, 即设置好问题的目标态. 电子科技大学 4 二. 条件及数据分析 设置好问题的目标态,着手工作还需要做以下工作: 1. 收集必要的资料和数据。 2. 分析现有的数据和 条件,使问题进一步明 确化。 例(96竞赛B) 节水洗衣机问题 电子科技大学 5 例(96竞赛B) 节水洗衣机问题 分析:题目中没有一个数据,但问题却需要比较多的数据及 条件,如 *衣服的洗净效果指标(包括污物和残留洗涤剂); *不同质地衣物的脱水率或衣物的含水量C; * 洗衣机的最高水位H、最低水位L; * 各类污物(泥土、油腻等)和洗涤剂在水中的溶解特性等。 电子科技大学 6 怎样收集数据和资料? 可在各类图书馆、网上查阅、向专家询问、通过试验来 得到。 收集数据应列入工作计划,并注意: 1. 向有关人员调查情况应事先设计好问题; 2. 事先确定所需资料清单、资料来源、收集方式。 有条理的收集计划可以为后期的工作 创造良好的条件 对收集到的或者现有的资料和数据要做仔细分析,使问题 进一步明确。 《数学建模》课件汇总 第27页,共105页

2021-12-28 《数学建模》课件汇总 例(96竞赛A)最优槽鱼策略 假设这种鱼分4个年龄组,称1龄鱼,“,4龄鱼。各年龄 组每条鱼的平均置量分别为 5.07,1155,17.86.22.99(克), 问题: 各年龄组鱼的自然死亡率均为0.8(1年), 这种鱼为季节性集中产卵禁殖,平均每条谢鱼的产卵 为了保护人类赖以生存的自然环境,可再生资 量为 源(如渔业、林业资源)的开发必须适度,一种合理、 1.109X105个), 简化的策略是,在实现可持续收获的前提下,追求 3前鱼的产哪量为这个数的一半,2前鱼和1前鱼不产 最大产量或最佳效益。 卵,产卵和解化期为每年的最后4个月,卵舞化并成活为 考虑对某种鱼的最优捕捞策略: 1龄鱼,成活率(1龄鱼条数与产卵总量n之比为 1.22X10u/(1.22×10+n) 海e行D可 e行t 分析:此圆中的数据、条件特别多,有的难于把漫,有 的会直接影响到所建模型是否正确。 迪业管理部门规定,每年只允许在产卵解化期 1.棉辨量度不取g 前的8个月内进行捕捞作业。如果年年投入的捕捞 单位时间槽捞量与鱼群条数成正比时的比例系数。 能力(如渔船数、下网次数等)圆定不变,这时单位时 间捕捞量将与各年龄组鱼群条数成正比,比例系数 可否理解为捕捞量占总鱼群量的百分率? 不妨称辅捞强度系数,通常使用13mm网眼的拉网,这 种网只能捕捞3龄鱼和4龄鱼,其两个捕捞强度系数 否! 之比为0.42:1,汕业上称这种方式为固定努力量捕捞。 将辅捞疆度系数?的定义用数学表达式写出。 N,)-N+)/M=gN) 令1一0,得到徽分方程 龄鱼在[,什△门时间段内由捕捞产生的变化量(捕捞 量)为 1=-4.9>0 N=-gN,或i N:(t)-Nt+) 思考: 单位时间的捕捞量是 1.此模型可与哪一个模型类比? Ni()-Ni(t+)/A 2.考虑g是否有单位? 对任何时间间隔山郁有 3.怎样理解捕捞提度系数? 。n月 神n 第28页,共105页 2
2021-12-28 2 电子科技大学 7 为 了 保 护 人 类 赖 以 生 存 的 自 然 环 境,可 再 生 资 源(如 渔 业、林 业 资 源)的 开 发 必 须 适 度,一 种 合 理、 简 化 的 策 略 是, 在 实 现 可 持 续 收 获 的 前 提 下,追 求 最 大 产 量 或 最 佳 效 益。 考 虑 对 某 种 鱼的 最 优 捕 捞 策 略: 例(96竞赛A) 最优捕鱼策略 电子科技大学 8 假 设 这 种 鱼 分 4 个 年 龄 组,称 1 龄鱼,…,4 龄 鱼。各 年 龄 组 每 条 鱼 的 平 均重 量 分 别 为 5.07, 11.55, 17.86, 22.99 (克), 各 年 龄 组 鱼 的 自然死亡率均 为 0.8 (1/年), 这 种 鱼 为 季 节 性 集 中 产 卵 繁 殖,平 均 每 条 4龄 鱼 的 产 卵 量 为 1.109×10 5(个), 3 龄 鱼 的 产 卵 量 为 这 个数 的 一 半,2 龄 鱼 和 1 龄 鱼 不 产 卵,产卵 和 孵 化 期为 每 年的 最 后 4 个 月,卵 孵化 并 成 活 为 1 龄 鱼,成 活 率(1 龄 鱼 条数 与 产 卵 总 量n 之 比 为 1.22×10 11 /(1.22×10 11+n) 电子科技大学 9 渔 业 管 理 部 门 规 定 ,每 年 只允 许 在 产 卵 孵 化 期 前 的 8 个 月 内进 行 捕 捞 作 业。如 果 每 年 投 入 的捕 捞 能 力(如 渔 船 数、下 网 次 数 等)固定不变,这时单位时 间 捕 捞 量 将 与 各 年 龄 组 鱼 群 条 数 成正 比,比 例 系 数 不 妨 称 捕捞强度系数,通 常 使 用 13mm 网 眼 的 拉 网,这 种网 只 能 捕 捞 3 龄 鱼 和 4 龄 鱼,其 两个 捕 捞 强 度 系 数 之 比 为 0.42:1,渔业 上 称 这 种 方 式 为 固 定 努 力 量 捕捞。 电子科技大学 10 可否理解为捕捞量占总鱼群量的百分率? 否! 分析:此题中的数据、条件特别多,有的难于把握,有 的会直接影响到所建模型是否正确。 1.捕捞强度系数 q 单位时间捕捞量与鱼群条数成正比时的比例系数。 电子科技大学 11 将捕捞强度系数 q 的定义用数学表达式写出。 设i龄鱼在[t ,t+Δt]时间段内由捕捞产生的变化量(捕捞 量)为 N (t) N (t t) i i 单位时间的捕捞量是 N t N t t t i( ) i( )/ 对任何时间间隔 Δt 都有 电子科技大学 12 N (t) N (t t)/ t qN (t) i i i 令 Δt 0 ,得到微分方程 , 0 1 q q dt dN N i i i qNi , 或 dt dN 2. 考虑 q 是否有单位? 思考: 1. 此模型可与哪一个模型类比? 3. 怎样理解捕捞强度系数q? 《数学建模》课件汇总 第28页,共105页

2021-12-28 《数学建模》课件汇总 2.面解现白摩r0.8(1/率)) 思考:请考虑在捕捞的情况下,鱼群数量变化的规律? 是否理解为鱼死亡的振率为0.8? 3.成赠卓C的响 不对 成活率c为1龄鱼条数与产卵总量n之比 类似于人口增长模型中的“自然(相对)增长率”,理解 e=122×10y(1.22×10+n) 为鱼群未受其他外界影响下的“自然增长率”。 设年的产卵量为m,则:+1年的1龄鱼数目为 即单位时间内死亡鱼的数量与鱼的总量之比,可得描述鱼群 N1(41)=nXc 自然死亡的徽分方程: 1=,ie12,34 Ni dt 22x10+n*n=12x10"/1+122x10 1.22×104 海…0D年 解行 因3、4龄鱼的数量级及产卵量的数量级分别是10和10叫 充分分析正确理解数据和条件可以进一步明确问题。 ◆n>>1.22X10川 →当n变动(即N,N(变动)时,N件1)的反应 还应该分析 不敏感 说明下一年1龄鱼的成活率使得鱼群对于捕捞量有一定 1.从数据中可得到什么信息? 的适应能力. 2.数据来源是否可靠? 3.所给条件有什么意义? 4.哪些条件是本质的? 5哪些条件是可以变动的?等等。 充分分析正确理解数据和条件可以进一步明确问愿。 还应该分析 1.从数据中可得到什么信息? 2.数据来源是否可靠? 3.所给条件有什么意义? 4.哪些条件是本质的? 5.哪些条件是可以变动的?簪等。 。行月 第29页,共105页 3
2021-12-28 3 电子科技大学 13 2. 自然死亡率r (0.8(1/年)) 是否理解为鱼死亡的概率为0.8 ? 不对! 类似于人口增长模型中的“自然(相对)增长率” ,理解 为鱼群未受其他外界影响下的“自然增长率” 。 即单位时间内死亡鱼的数量与鱼的总量之比,可得描述鱼群 自然死亡的微分方程: , 1,2,3,4; 1 r i dt dN N i i 电子科技大学 14 思考: 请考虑在捕捞的情况下,鱼群数量变化的规律? 3. 成活率c的影响 成活率c为1龄鱼条数与产卵总量n之比 c =1.22×1011 /(1.22×1011+n) 设t年的产卵量为n,则t + 1年的1 龄鱼数目为 N1(t+1)= n × c ) 1.22 10 1.22 10 /(1 1.22 10 1.22 10 11 11 11 11 n n n 电子科技大学 15 当 n 变动(即N3(t),N4(t)变动)时,N1(t+1)的反应 不敏感. 因3、4龄鱼的数量级及产卵量的数量级分别是109和1014 n>>1.22×1011 说明下一年1龄鱼的成活率使得鱼群对于捕捞量有一定 的适应能力.N10 n 电子科技大学 16 5. 哪些条件是可以变动的?等等。 2. 数据来源是否可靠? 3. 所给条件有什么意义? 4. 哪些条件是本质的? 充分分析正确理解数据和条件可以进一步明确问题。 还应该分析 1. 从数据中可得到什么信息? 电子科技大学 17 5. 哪些条件是可以变动的?等等。 2. 数据来源是否可靠? 3. 所给条件有什么意义? 4. 哪些条件是本质的? 充分分析正确理解数据和条件可以进一步明确问题。 还应该分析 1. 从数据中可得到什么信息? 《数学建模》课件汇总 第29页,共105页
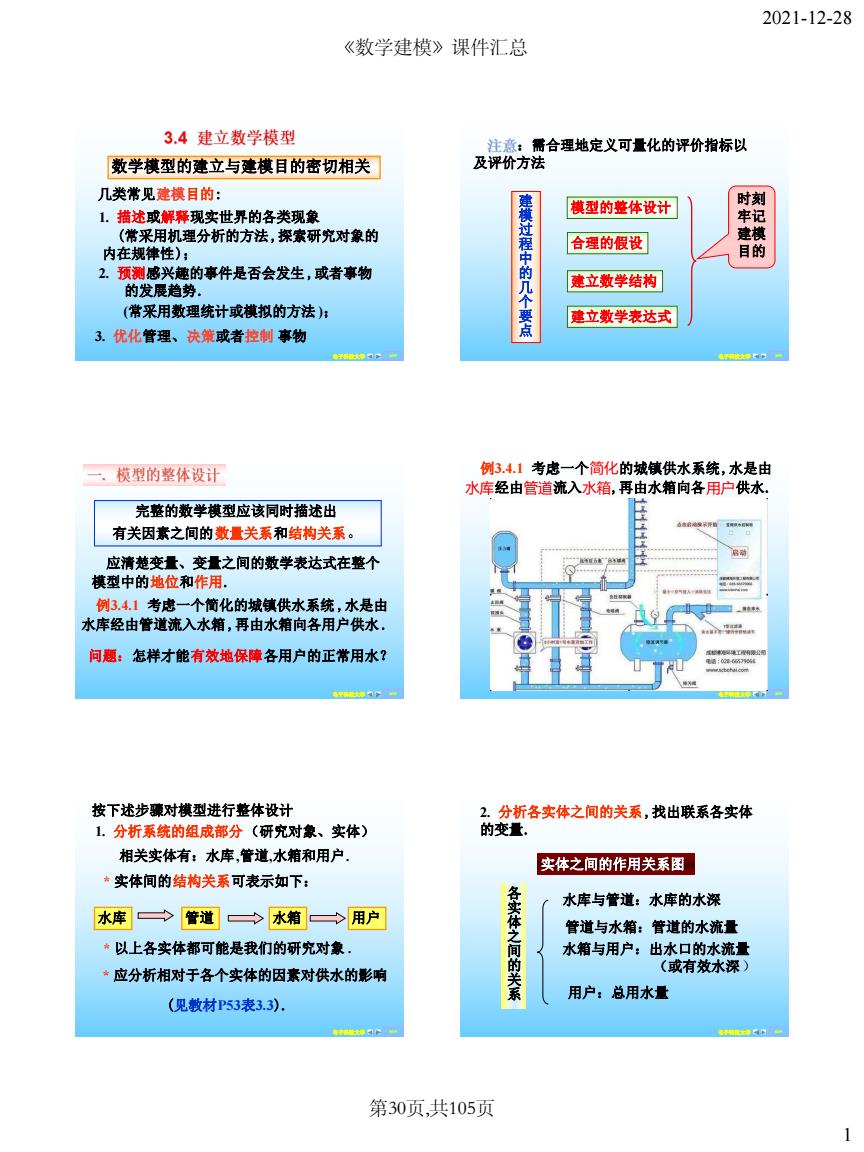
2021-12-28 《数学建模》课件汇总 3.4建立数学模型 注意:需合理地定义可量化的评价指标以 数学模型的建立与建模目的密切相关 及评价方法 几类常见建模目的: 模型的整体设计 时刻 1.描述或解释现实世界的各类现象 (常采用机理分析的方法,探索研究对象的 内在规律性): 建棋过程中 合理的假设 建模 目的 2.预测感兴趣的事件是否会发生,或者事物 的发展趋势. 建立数学结构 (常采用数理统计或棋拟的方法) 几个要点 建立数学表达式 3.优化管理、决策或者控制事物 塘白管物 确◆上行常 一.模型的整体设计 例3.4.1考虑一个简化的城镇供水系统,水是由 水库经由管道流入水箱,再由水箱向各用户供水. 完整的数学模型应该同时描述出 有关因素之间的数量关系和结构关系。 应清楚变量、变量之间的数学表达式在整个 模型中的地位和作用。 例3.41考虑一个简化的城镇供水系统,水是由 水库经由管道流入水箱,再由水箱向各用户供水, 问题:怎样才能有效地保障各用户的正常用水? 按下述步骤对模型进行整体设计 2.分析各实体之间的关系,找出联系各实体 1.分析系统的组成部分(研究对象、实体) 的变量. 相关实体有:水库,管道,水箱和用户。 实体之间的作用关系图 *实体间的结构关系可表示如下: 水库与管道:水库的水深 水库→管道→水箱>用户 各实体之 管道与水箱:管道的水流量 *以上各实体都可能是我们的研究对象, 水箱与用户:出水口的水流量 *应分析相对于各个实体的因素对供水的影响 的关系 (或有效水深) 用户:总用水量 (见教材P53表3.3), 移自上零 球长的常 第30页,共105页 1
2021-12-28 1 电子科技大学 1/19 数学模型的建立与建模目的密切相关 几类常见建模目的: 1. 描述或解释现实世界的各类现象 (常采用机理分析的方法,探索研究对象的 内在规律性); 2. 预测感兴趣的事件是否会发生 ,或者事物 的发展趋势. (常采用数理统计或模拟的方法 ); 3. 优化管理、决策或者控制 事物 电子科技大学 2/19 :需合理地定义可量化的评价指标以 及评价方法 建 模 过 程 中 的 几 个 要 点 模型的整体设计 合理的假设 建立数学表达式 建立数学结构 时刻 牢记 建模 目的 电子科技大学 3/19 完整的数学模型应该同时描述出 有关因素之间的数量关系和结构关系。 应清楚变量、变量之间的数学表达式在整个 模型中的地位和作用. 例3.4.1 考虑一个简化的城镇供水系统 ,水是由 水库经由管道流入水箱,再由水箱向各用户供水. 问题:怎样才能有效地保障各用户的正常用水? 电子科技大学 4/19 例3.4.1 考虑一个简化的城镇供水系统,水是由 水库经由管道流入水箱,再由水箱向各用户供水. 电子科技大学 5/19 按下述步骤对模型进行整体设计 1. 分析系统的组成部分(研究对象、实体) 相关实体有:水库,管道,水箱和用户. * 实体间的结构关系可表示如下: 水库 管道 水箱 用户 * 以上各实体都可能是我们的研究对象 . * 应分析相对于各个实体的因素对供水的影响 (见教材P53表3.3). 电子科技大学 6/19 实体之间的作用关系图 各 实 体 之 间 的 关 系 管道与水箱:管道的水流量 水库与管道:水库的水深 水箱与用户:出水口的水流量 (或有效水深) 用户:总用水量 2. 分析各实体之间的关系,找出联系各实体 的变量. 《数学建模》课件汇总 第30页,共105页