南京大学：《电动力学 Electrodynamics》课程教学资源（课件讲稿）第四章 电磁波的传播 Propagation of Electromagnetic Wave

-VE=02uE 令 ⑩28=k2 可得 V2E+k2E=0 亥姆霍兹方程 V.E=0 B 可由 B=-VxE 求出 ) 11

2 2   E E   令 2 2    k 可得 2 2 0 0 E k E E      亥姆霍兹方程 i B E   B 可由   求出 11

归纳如下： V2E+k2E=0 V2B+k2B=0 7.龙=0 V.B=0 B=V×E E ouE 小结：电磁波在介质中的传播满足亥姆霍兹方程， 其解即显示了电磁波在介质中如何传播。 12

2 2 0 0 E k E E i B E               2 2 0 0 B k B B i E B                归纳如下: 小结：电磁波在介质中的传播满足亥姆霍兹方程， 其解即显示了电磁波在介质中如何传播。 12

3、平面电磁波 平面波定义： 波阵面与波矢垂直的平面，平面上的点相位相等。 亥姆霍兹方程： V2E+k2E-0 它的一个解是 E()=Eelk 其中E是常矢量 13

3、平面电磁波 平面波定义： 波阵面与波矢垂直的平面，平面上的点相位相等。 2 2 亥姆霍兹方程：    E k E 0 它的一个解是   0 ik x E x E e   其中 E0 是常矢量 13

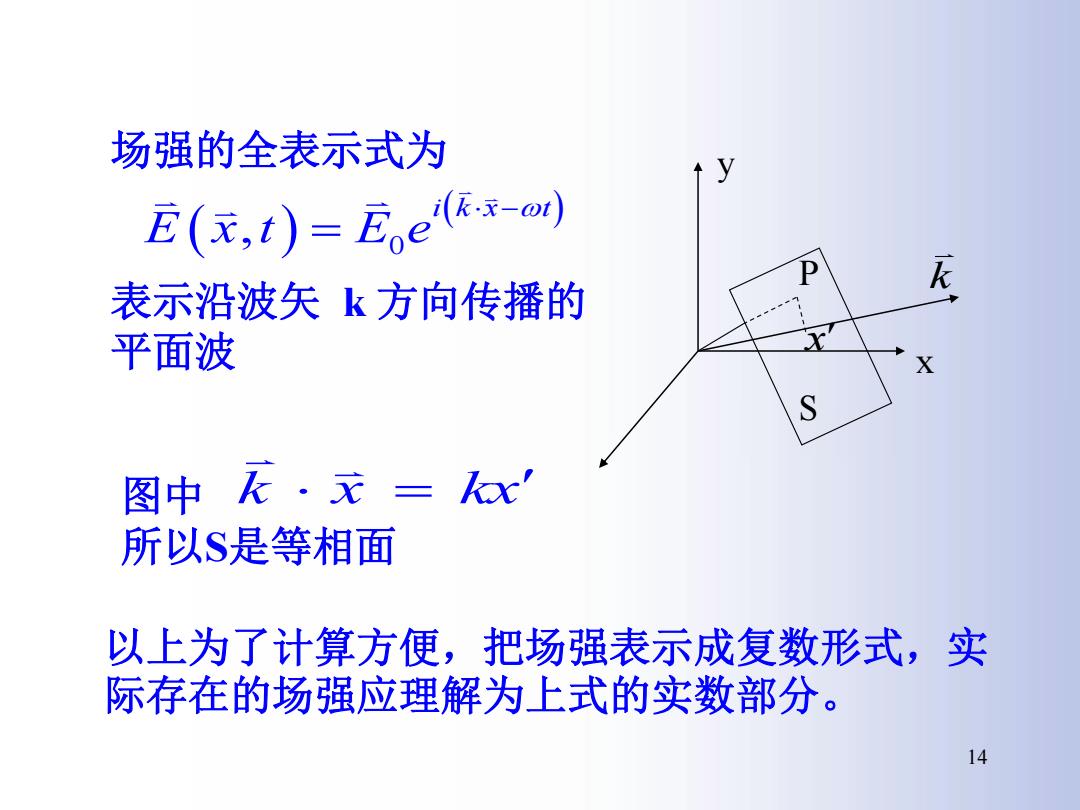
场强的全表示式为 E(元，t)=Ee(kx-o) D 表示沿波矢k方向传播的 平面波 X S 图中飞·x= 所以S是等相面 以上为了计算方便，把场强表示成复数形式，实 际存在的场强应理解为上式的实数部分。 14

S P y x k x  场强的全表示式为 表示沿波矢 k 方向传播的 平面波 图中 所以S是等相面     0 , i k x t E x t E e    k x kx    以上为了计算方便，把场强表示成复数形式，实 际存在的场强应理解为上式的实数部分。 14

实部： E(c,)=瓦cos(k·t-ox） k方向代表波传播的方向，数值k称为圆波数。 由于飞·x=x'沿电磁波传播方向相距为 △x'=2π/k的两点有相位差2π，因此这两点的 距离即为波长九， 2π 九= 2π k= k 九 15

2 k    k 方向代表波传播的方向，数值k称为圆波数。 E x t E k x t ( , ) cos    0    由于 沿电磁波传播方向相距为 的两点有相位差 ，因此这两点的 距离即为波长 ， k x kx    2  2 k      x k  2 /  实部： 15