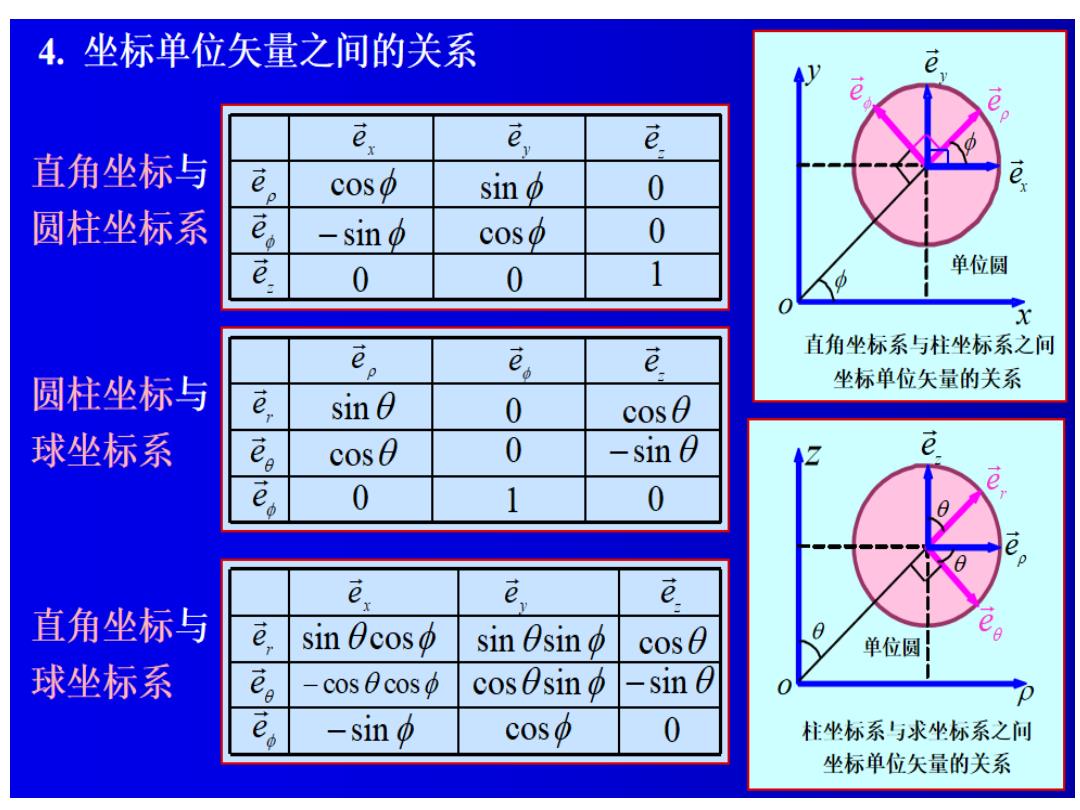
4.坐标单位矢量之间的关系 e e e 直角坐标与 e cos中 sin 0 圆柱坐标系 -sin o coso 0 e 0 0 单位圆 e。 e。 e 直角坐标系与柱坐标系之间 圆柱坐标与 坐标单位矢量的关系 e sin 0 cos0 球坐标系 e。 cos0 0 -sin e 0 1 0 e e e, e 直角坐标与 sin 0coso sin Osino cos0 单位圆 球坐标系 g cos 0 coso cosθsin0 -s1nθ -sin o cos中 0 柱坐标系与求坐标系之问 坐标单位矢量的关系
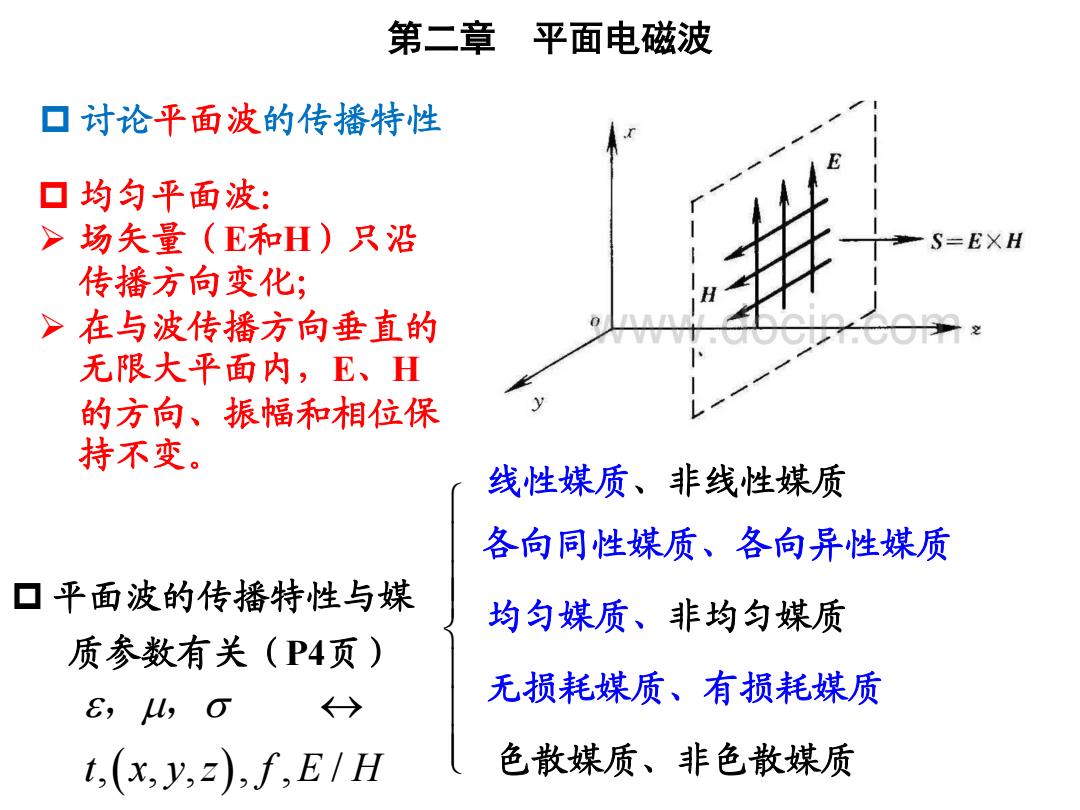
第二章 平面电磁波 ▣讨论平面波的传播特性 ▣均匀平面波: >对 场矢量(E和H)只沿 S=EXH 传播方向变化; > 在与波传播方向垂直的 无限大平面内,E、H 的方向、振幅和相位保 持不变。 线性媒质、非线性媒质 各向同性媒质、各向异性媒质 口平面波的传播特性与媒 均匀媒质、非均匀媒质 质参数有关(P4页) 无损耗媒质、有损耗媒质 &L,O ←→ t,(x,y,2),f,E/H 色散媒质、非色散媒质
平面波的传播特性与媒 质参数有关(P4页) 均匀媒质、非均匀媒质 各向同性媒质、各向异性媒质 无损耗媒质、有损耗媒质 线性媒质、非线性媒质 色散媒质、非色散媒质 讨论平面波的传播特性 第二章 平面电磁波 均匀平面波: ➢ 场矢量(E和H)只沿 传播方向变化; ➢ 在与波传播方向垂直的 无限大平面内,E、H 的方向、振幅和相位保 持不变。 t x y z f E H , , , , , / ( ) , ,
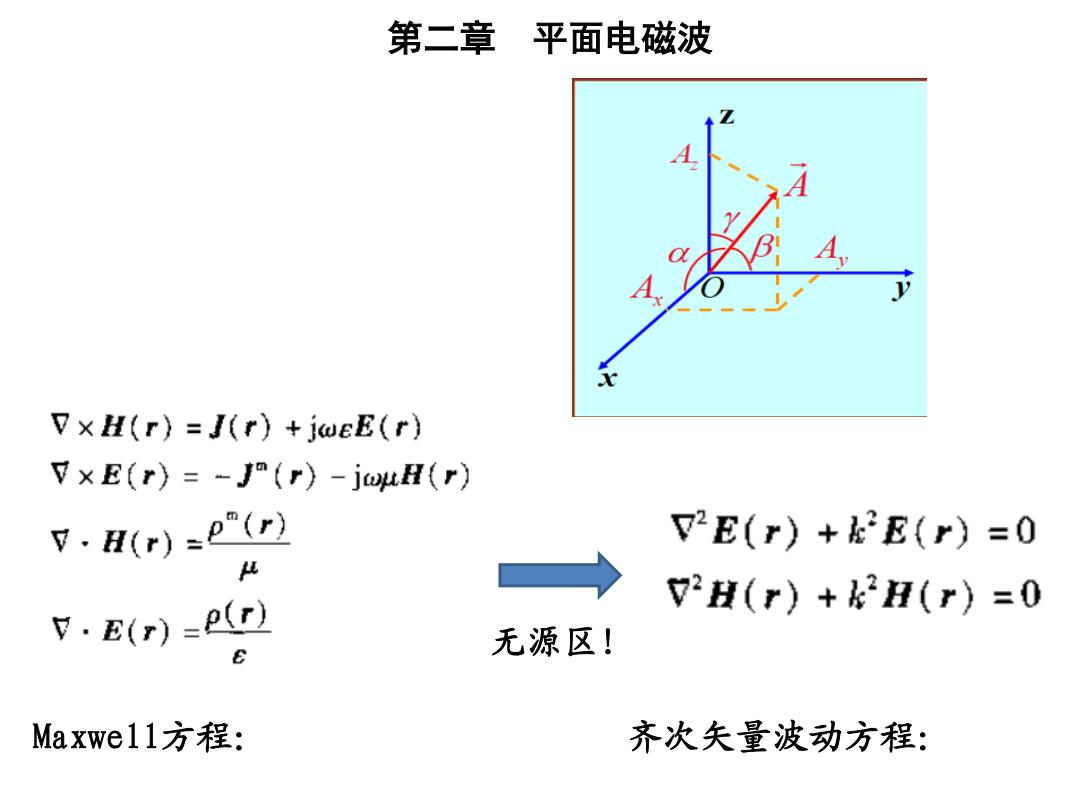
第二章平面电磁波 又×H(r)=J(r)+jeE(r) V×E(r)=-J(r)-juH(r) V.H(r)=e"(r) V2E(r)+kE(r)=0 4 V.E(r)=e(r) V2H(r)+k2H(r)=0 无源区」 Maxwe11方程: 齐次矢量波动方程:
第二章 平面电磁波 Maxwell方程: 齐次矢量波动方程: 无源区!

第二章平面电磁波 ▣分析条件 ←〉 >无限大,各向同性、均匀、线性、 理想介质中 t.(x.v,=f,E/H 无源区内,正弦电磁场(时谐电磁场) 在无源区中,又·E=0,·H=0 在有源区内,又·E-卫,VH=2 & 满足齐次矢量Helmholtz方程: V2E(r)+2E(r)=0 V2H(r)+k2H(r)=0 鞋 传播常数:k。=o√ue。 等效介电常数:8=8一了0
第二章 平面电磁波 分析条件 ➢ 无限大,各向同性、均匀、线性、 理想介质中 ➢ 无源区内,正弦电磁场(时谐电磁场) 满足齐次矢量Helmholtz方程: t x y z f E H , , , , , / ( ) , , ( ) ( ) ( ) ( ) 2 2 2 2 0 0 c c E r k E r H r k H r + = + = c e e k j = = − 传播常数: 等效介电常数: 齐次 矢量 波动 方程
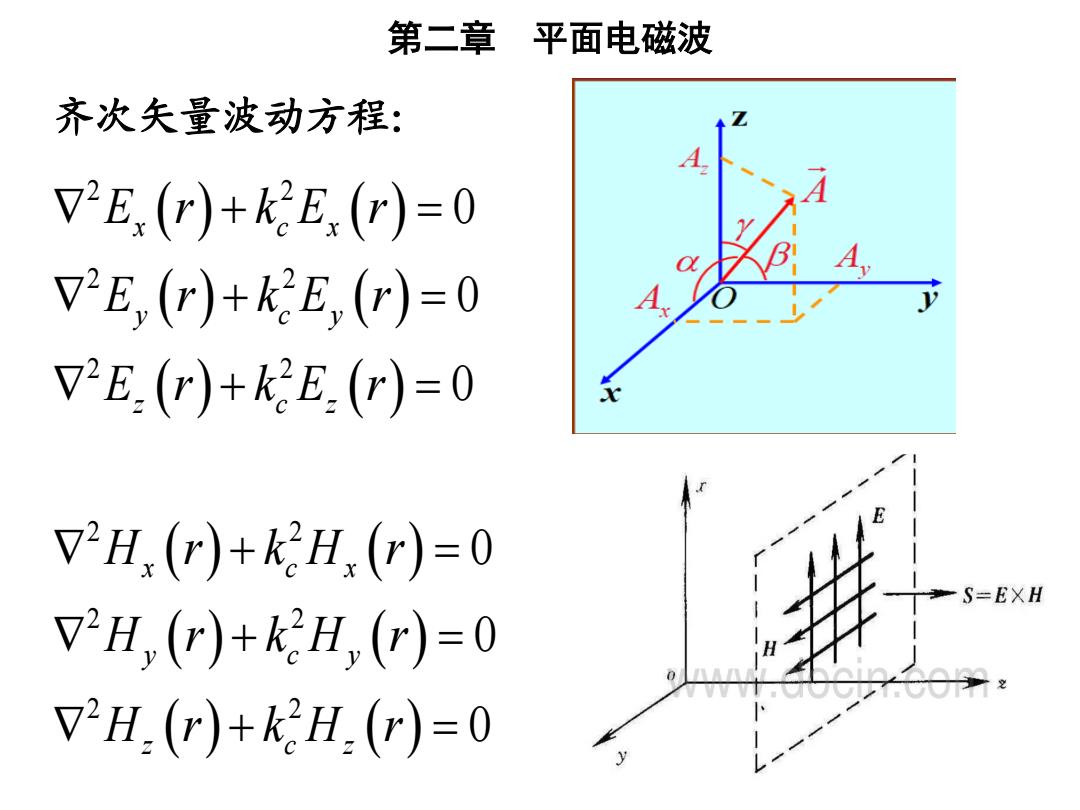
第二章 平面电磁波 齐次矢量波动方程: V2E,(r)+k2E,(r)=0 V2E,(r)+kE,()=0 v2E.(r)+k2E(r)=0 V2H(r)+k2H(r)=0 S=EXH V2H,(r)+k2H,(r)=0 V2H.(r)+k2H.(r)=0
第二章 平面电磁波 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 2 2 2 2 2 2 2 2 2 2 2 2 0 0 0 0 0 0 x c x y c y z c z x c x y c y z c z E r k E r E r k E r E r k E r H r k H r H r k H r H r k H r + = + = + = + = + = + = 齐次矢量波动方程: