§141磁场与磁感应强度 第十四章稳恒嫩场 一、基本磁现象 §14-1嫩场与做感应强皮 平都D §14-2华一萨定律及应用 §14-3赚场的高新定理和安培环路定理 §14-4赚场对电流的作用 §14-5狮电粒子的运动 在观察的领域帝,机遇只偏爱那种有准备的头脑! 龙周道合 官合■■■■■■ 产生磁作用(磁现象)的“源”: √运动电荷周围既有电场又有磁场 1运动电荷 *电荷周围的场 2.传导电流 讨论 [S] 与观测者所处 7=0 3.永磁体(分子电流) 的参照系有关 [S1 ·B=0 结论:一切磁现象起源于电荷的运动。 (电流) ·磁作用以慰场为煤介,通过磁场实现磁作用的传递 B≠0 ·运动电荷、传导电流、永磁体都可以产生磁场 *Dirac Magnetic Monopole (磁单极) 磁场又对三者产生(磁)作用—磁力 磁单极的观测与对理论体系的影响 合≤■■■ ■■■■■■■看
1 第十四章 稳恒磁场 §14-2 毕-萨定律及应用 §14-1 磁场与磁感应强度 §14-4 磁场对电流的作用 §14-3 磁场的高斯定理和安培环路定理 §14-5 带电粒子的运动 SKIP §14-1 磁场与磁感应强度 一、基本磁现象 志同道合 在观察的领域中,机遇只偏爱那种有准备的头脑! 产生磁作用(磁现象)的“源”: 1.运动电荷 2.传导电流 3.永磁体 (分子电流) 结论:一切磁现象起源于电荷的运动 。 (电流) •运动电荷、传导电流、永磁体都可以产生磁场 •磁场又对三者产生(磁)作用 —— 磁力 •磁作用以磁场为媒介,通过磁场实现磁作用的传递 r V Q [ ] S′ r r ′ = ′ = V B 0 0 [ ] S r B ≠ 0 *运动电荷周围既有电场又有磁场 *电荷周围的场 与观测者所处 的参照系有关 *Dirac Magnetic Monopole (磁单极) 磁单极的观测与对理论体系的影响 讨论

二、磁感强度 2.1,F1B 描述磁场的物理量一磁感应强度—B =P 规定:磁场中小磁针N极指向为磁感应强度的方向! 即FL了,B构成之平面。 根据运动电荷在磁场中受力情况来确定磁场的性质 简记为:F位×B) 实验结论: 1 另q→-q→F→-F 1.7=0则F=0: 了≠0,一般F≠0, P B 但电荷沿某特定方向运动时,则F=0 度位厅下■ ■■■ 3. Fo lay sine 3.Fcclqv sine 1 1 rsn点g,y.0无关,2q 9pm与g.',0无关,2 0 B B p T8 只与位置有关。一 只与位置有关。 定义:B=F/ vsino 定义:B= F/ qV sin →FIg(x) →F=BlqV sine 结合FI9(xB) →F=q(0×B) q -洛仑兹(LORENTZ)磁力公式 合≤■■■ ■■■■■■■看 2
2 x y z q p r F θ r B r V o 根据运动电荷在磁场中受力情况来确定磁场的性质 F = 0 r 但电荷沿某特定方向运动时,则 实验结论: r V = 0 r 1. 则 F = 0; 二、磁感强度 r F ≠ 0 r V ≠ 0,一般 , 规定:磁场中小磁针N极指向为磁感应强度的方向! 描述磁场的物理量 —— 磁感应强度—— B r q q F F r r 另 → − ⇒ → − x y z q p r F θ r B r V o r r r 即 构成之平面。 FVB ⊥ , r r r r 2. FV FB ⊥ ⊥ , . F (V B) r r r 简记为: // × // (V B) q q F r r r × F ∝ qV sinθ r 3. q V sin θ F r 与 无关, q V, ,θ qV sinθ 定义:B = F 只与位置有关。 // (V B) q q F r r r × x y z q p r F θ r B r V o F = B qV sinθ // (V B) q q F r r r 结合 × F q(V B) r r r = × —洛仑兹(LORENTZ)磁力公式 F ∝ qV sinθ r 3. q V sin θ F r 与 无关, q V, ,θ qV sinθ 定义:B = F 只与位置有关。x y z q p r F θ r B r V o
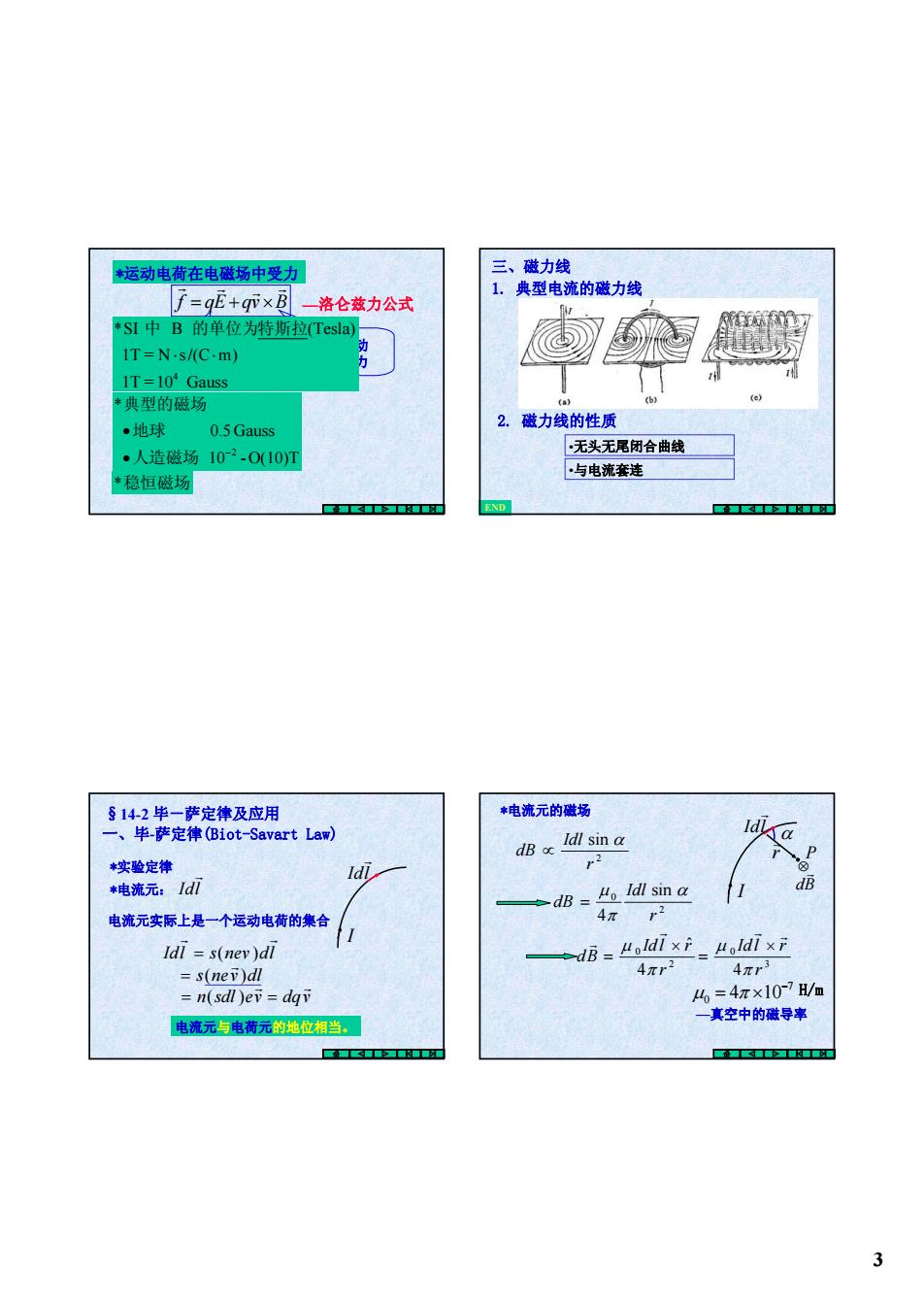
运动电荷在电磁场中受力 三、磁力线 f=9乖+9Tx目 1.典型电流的磁力线 一洛仑兹力公式 *SI中B的单位为特斯拉(Tesla) IT=N.s/(C.m) IT=10 Gauss *典型的磁场 (a) (e) ·地球 0.5 Gauss 2. 磁力线的性质 ·人造磁场102-0(10)T ·无头无尾闭合曲线 ·与电流套连 *稳恒磁场 属位厅5国 END ■合■■■■ §14-2毕-萨定律及应用 *电流元的磁场 一、毕-萨定律(Biot-Savart Law)) dB Idl sin a P 实验定律 Idl r2 ⑧ *电流元:Idl →dB=。Idl sin dB 电流元实际上是一个运动电荷的集合 4π r2 Idl =s(nev)dl dB=Holdl xf Holdl xF =s(nev)dl 4πr2 4πr3 n(sdl )e=dg 4=4π×10-7H/m —真空中的磁导率 电流元与电荷元的地位相当。 合≤■■■ ■■■■■■■看 3
3 f qE qv B r r r r = + × *运动电荷在电磁场中受力 —洛仑兹力公式 10 -O(10)T 0.5 Gauss * −2 • • 人造磁场 地球 典型的磁场 *稳恒磁场 电场力,与电荷 的运动状态无关 磁场力,运动 电荷才受磁力 1T =10 Gauss 1T = N s/(C m) *SI B (Tesla) 4 ⋅ ⋅ 中 的单位为特斯拉 •无头无尾闭合曲线 1. 典型电流的磁力线 •与电流套连 三、磁力线 2. 磁力线的性质 END 一、毕-萨定律(Biot-Savart Law) Idl r I Idl r §14-2 毕-萨定律及应用 *实验定律 *电流元: 电流元实际上是一个运动电荷的集合 Idl s nev dl r r = ( ) s(nev )dl r = n sdl ev r = ( ) dqv r = 电流元与电荷元的地位相当。 2 sin r Idl dB α ∝ 7 0 4 10− μ = π × H/m —真空中的磁导率 I Idl r P r r α ⊗ dB r *电流元的磁场 2 0 4 ˆ r Idl r dB π μ × = r r 2 0 sin 4 r Idl dB α π μ = 3 0 4 r Idl r π μ r r × =
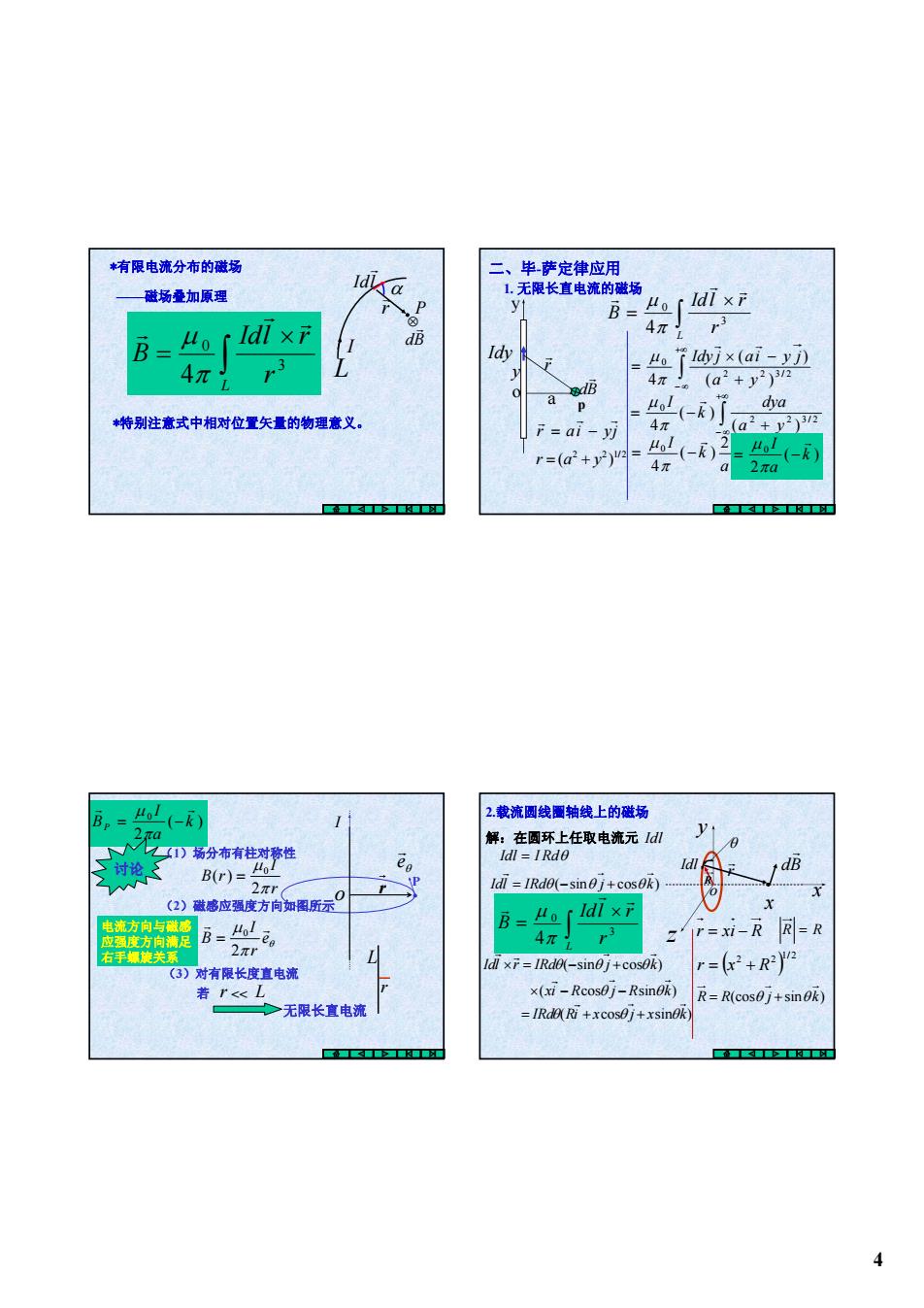
*有限电流分布的磁场 二、毕萨定律应用 磁场叠加原理 1.无限长直电流的磁场 B=Ho ldTx B=Ho ldl×f dB 4π Idy 4。f7x(ai-y 4π dB 4π。 (a2+y2)32 a p dya 特别注意式中相对位置矢量的物理意义。 (-) F=ai-yj 4π (a2+y2)32 r=(a+y2)= -) 4π a o(-) 2πa 度■ ■合■■■■ Br= L(-) 2.载流圆线圈轴线上的磁场 2a 解:在圆环上任取电流元1d机 入D场分布有柱对称性 三讨论 Idl=IRd0 Idl B(r)= 2πr r P Idl IRd0(-sin0j+cos0k) (2)做感应强度方向如图所示 ldl×F 电流方向与散感 应强度方向满足 B=41 B=Ho 4π r=xi-R凤=R 右手螺娘关系 2πr (3)对有限长度直电流 ldl x=IRde(-sin0j+cosok) r=2+R2 若r<L x(xi-Rcos0j-RsinOk) R=R(cos0j+sin0k) >无限长直电流 IRde(Ri +xcosej+xsinek ■位≤■■■■■ ■■■■■■■香
4 ∫ × = L r Idl r B 3 0 4 r r r π μ *有限电流分布的磁场 ——磁场叠加原理 *特别注意式中相对位置矢量的物理意义。 I Idl r P r r α ⊗ dB r L 1. 无限长直电流的磁场 y o y Idy r r 二、毕-萨定律应用 a . p r ai yj r r r = − 2 2 1/ 2 r = (a + y ) dB r ∫ × = L r Idl r B 3 0 4 r r r π μ ∫ +∞ − ∞ + × − = 2 2 3 / 2 0 ( ) ( ) 4 a y Idy j ai y j r r π μ ∫ +∞ − ∞ + = − 2 2 3 / 2 0 ( ) ( ) 4 a y dya k I r π μ a k I 2 ( ) 4 0 r = − π μ ( ) 2 0 k a I r = − π μ ( ) 2 0 k a I BP r r = − π μ L r 无限长直电流 讨论 (1)场分布有柱对称性 r I B r π μ 2 ( ) 0 = (2)磁感应强度方向如图所示 (3)对有限长度直电流 若 r << L θ e r θ π μ e r I B r r 2 0 = o r . P I 电流方向与磁感 应强度方向满足 右手螺旋关系 2.载流圆线圈轴线上的磁场 解:在圆环上任取电流元 Idl r = xi − R R = R x y z o x dB r R Idl = I Rdθ ( )1/ 2 2 2 r = x + R R = R(cosθ j + sinθ k) θ r r Idl Idl = IRdθ (−sinθ j + cosθ k) r ∫ × = L r Idl r B 3 0 4 r r r π μ ( cos sin ) ( sin cos ) xi R j R k Idl r IRd j k θ θ θ θ θ × − − × = − + r r r = IRdθ(Ri + xcosθ j + xsinθk) r

B=凸f IRde[Ri +x cosj+xsin HoIR2 Pe 4π (R2+x2)32 2(R2+x2)3/2 2π6r IRdORi dB 若X>R HoIR2 4π(R2+x2)亚 子 →B= 2r3 LoIR 行=xi-R风=R 定义:pn=I(πR2)i B=“D 2(R2+x2)迈 osek) r=62+R22 若x=0 23 沿轴线方向1 电沐绕向与碱多 0j-Rsin0k) R=R(cos0j+sin0k) →B=4l 磁偶极子、磁偶极矩 应强度方向满足 cosj+xsink) 2R 右手规则1 度■■ 官金■■■■ 3.无限长爆线管轴线上的磁场 4.均匀带电圆盘(σ),以o旋转。求盘心 R dB。= oR(nldx) 磁场和总磁矩。 2(R2+x23 电荷元:dg=o2πrd + 沿x方向I MoR'nldx 圆电流:d山=d西-o o2πrd ◇B。= T2π 2(R2+x2)3 =uonl =oo rdr +R 无限长螺线管轴线上的磁场是均内的。 dB=dI=Ho dr 实际上:无限长娜绒管内磁场是均匀的 2r2 B= LoIR 2(R2+x2)D ND 位口下■ ■■■■■■■看 5
5 ( cos sin ) ( sin cos ) xi R j R k Idl r IRd j k θ θ θ θ θ × − − × = − + r r r r = xi − R R = R x y z o x dB r R ( )1/ 2 2 2 r = x + R R = R(cosθ j +sinθ k) θ r r Idl = IRdθ(Ri + xcosθ j + xsinθk) r ∫ + + + = L R x IRd Ri x j x k B 2 2 3/ 2 0 ( ) [ cos sin ] 4 r r r r θ θ θ π μ ∫ + = L R x IRd Ri 2 2 3/ 2 0 4 ( ) r θ π μ i R x IR r 2 2 3/ 2 2 0 2( + ) = μ 沿轴线方向! 电流绕向与磁感 应强度方向满足 右手规则! 若 x >> R 若 x = 0 x y z o x i R x IR B r r 2 2 3/ 2 2 0 2( + ) = μ i x IR B r r 3 2 0 2 μ = i R I B r r 2 μ 0 = 定义:p I R i m r r ( ) 2 = π 3 0 2 x p B m π μ r r = 3 0 2 r p E e πε r r = 磁偶极子、磁偶极矩 3. 无限长螺线管轴线上的磁场 ( ) 2 3 2 2 2 0 2(R x ) R nIdx dBO + = μ ∫ +∞ −∞ + = 2 3 2 2 2 0 2(R x ) R nIdx BO μ nI = μ0 x R n 沿 x 方向! 无限长螺线管轴线上的磁场是均匀的。 实际上:无限长螺线管内磁场是均匀的! i R x IR B r r 2 2 3/ 2 2 0 2( + ) = μ END x O dx . 4.均匀带电圆盘(σ) ,以ω旋转。求盘心 磁场和总磁矩。 dq = σ 2π rdr dB dI r = μ0 2 ∫ B = dB R r dr 电荷元: T dq 圆电流:dI = 2 rdr 2 σ π π ω= = ωσ rdr ∫ = R dr 0 0 2 μ ωσ μ0 σωR 2 1 = dr 2 μ0ωσ =