
好玩的数学 中国古算解趣 晦而彰”(永嘉陈几先《日用算法》跋)。一生著作甚多,但散 失严重。现存有:《详解九章算法》(1261年)、《详解算法》 (1262年)、《乘除算法通宝》(1274年)、《续古算法摘奇》 (1275年)、《田亩比类乘除捷法》(1275年)等。 杨辉对“九宫图”进行了深入的研究,并把它命名为《纵 横图》,从三阶推广到高阶,取得了一系列重要的成果。现在 人们习惯地把纵横图称为幻方。所谓n阶幻方,就是把1至 n2个自然数排成n行、n列的方阵,使它的每行、每列和每 条对角线上数的和都相等。九宫图就是一个三阶幻方,杨辉给 出了编制的方法。 对于四阶幻方可以沿三阶的思路,也不难构造。 方阵斜排 上下对易 左右相更 转正放平 1 16 16 5 2 5 个、2 52 49516 96 911、3 911、3 147112 1310 7 1310 7> 4 47 10>13 1411/ 8 146/ 146 8 156103 15 12 15 12 15 12 112813 16 1 注意:中间虚线构成的小正方形,也进行上下对易和左右 相更的变换,求其平衡,使各行各列和主对角线各数字之和相 等。 对于n=5的情况,可以拓宽思路,用类似的方法构造5 阶幻方。 各子斜排以后,确定核心正方形11,3,15,23,形外的 上、下、左、右四块,通过对易和相更,整体移入形内,就得 到一个五阶幻方。当然,研究问题的路子是多种多样的,同学 们可以充分发挥自己的创造力,“八仙过海,各显神通”。 18
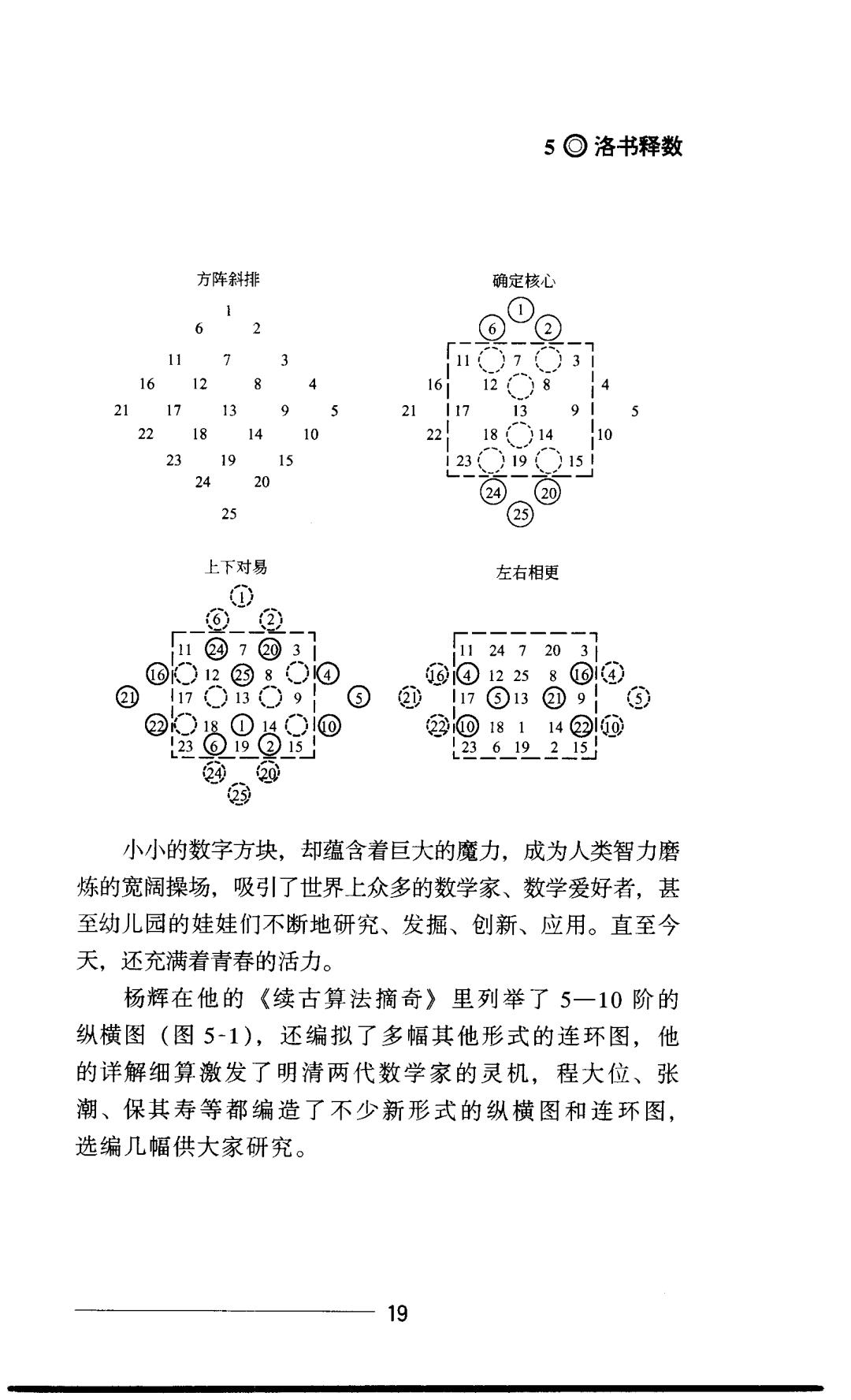
5○洛书释数 方阵斜排 确定核心 ① 6 2 ⑥ 2 117 3 1612 8 4 1612(○)8 14 211713 95 11713 91 2218 1410 22 18○14 10 23 19 15 23○19○)15 24 20 24 ②D 35 ②⑤ 上下对易 左右相更 ① 回② @71 124720 31 ⑥02国8○1④ ⑥1④1225 8( ⑥14 ④ 117 C13○9| ⑤ ⑩ I17⑤13 @9③ ②K○18①4○⑩ 221⑩18114Q②10 L23⑥19②15 L23619215 2 20 2⑧ 小小的数字方块,却蕴含着巨大的魔力,成为人类智力磨 炼的宽阔操场,吸引了世界上众多的数学家、数学爱好者,甚 至幼儿园的娃娃们不断地研究、发掘、创新、应用。直至今 天,还充满着青春的活力。 杨辉在他的《续古算法摘奇》里列举了5一10阶的 纵横图(图5-1),还编拟了多幅其他形式的连环图,他 的详解细算激发了明清两代数学家的灵机,程大位、张 潮、保其寿等都编造了不少新形式的纵横图和连环图, 选编几幅供大家研究。 19
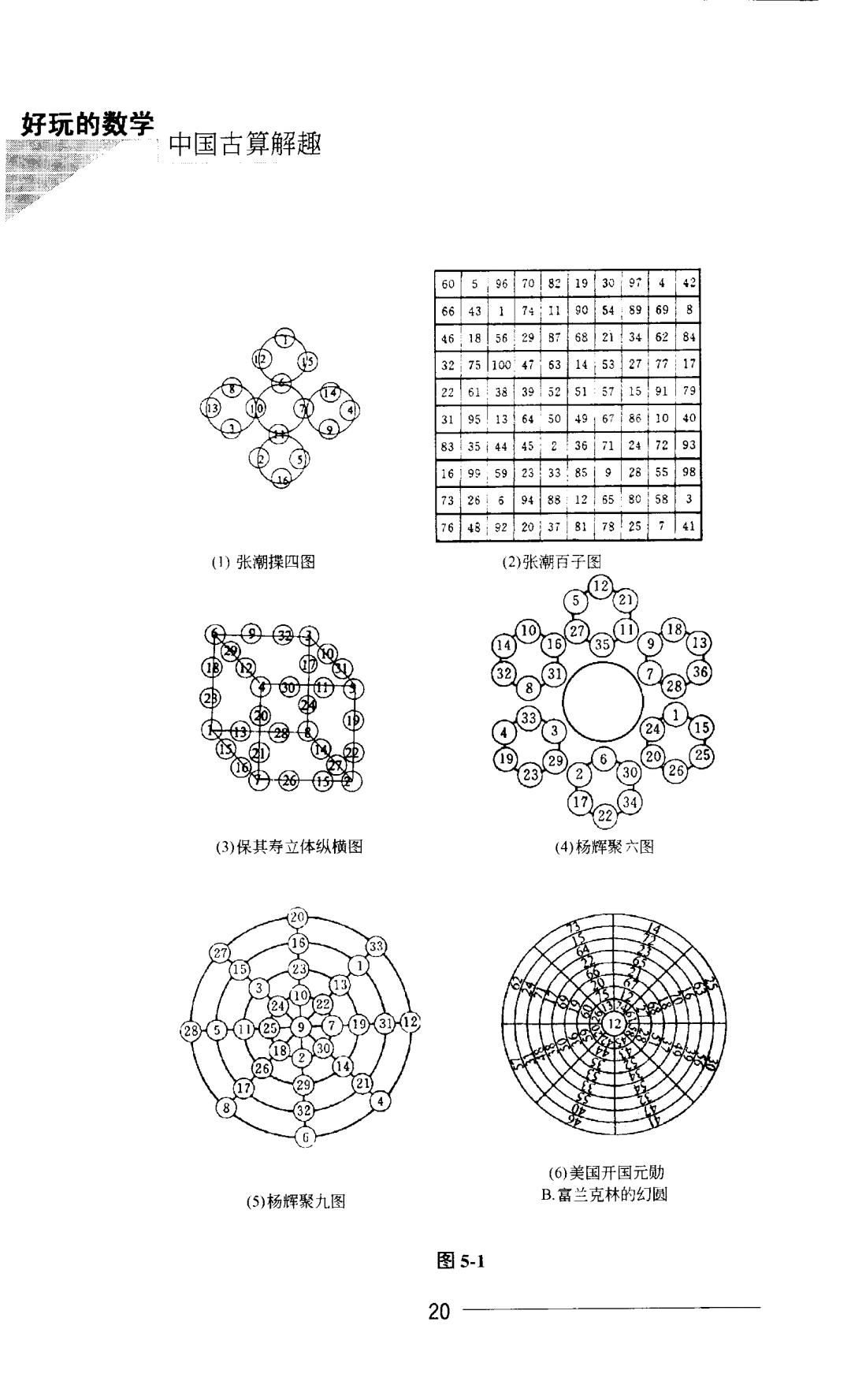
好玩的数学 中国古算解趣 60 5967082193097442 66 431 74;11 9054:89698 ⑤ 56 87 34 62 84 32 75100 47 53 14:53 277717 ⑧ 61383952 51:57159179 的 31 9513 64 50 49167 8610 40 母 83 3544 45 2 3671 2472 93 1699,59 2333 :8592855 98 73 26 6 9488:126580 58 3 76 4892 2037817825741 ()张潮揲四图 (2)张潮百子图 o e④ ⑨®® ©@ ⑧ ⑧ ⑧ 过 ③⊙ ⑨ D 西 @ (3)保其寿立体纵横图 (4)杨辉聚六图 20 33 15 3 3 28⑤①2⑤9⑦©③2 26 14 17 29 8 32 4 (6)美国开国元勋 (5)杨辉聚九图 B.富兰克林的幻圆 图5-1 20

5◎洛书释数 图5-1(6)中: ①八个同心圆上八个数(连同中心数)的和是360。 ②八条半径上九个数的和都是360。 ③相邻四格(不论在什么位置)中元素和连同中心数之半 都是180。 读读练练 练 习题 请你再排一个四阶幻方和五阶幻方(取数12~75)。 21

6竿索求长 一枝竹竿一条索 索比竿子长一托 对折索子来量竿却比竿子短一托 答曰:竿长一大五尺,泉长二丈 选自《算法统宗》 “托”是民间丈量绳子长度的一种常用方法,一般为平伸 二臂、两中指间的距离。《算法统宗》中认定1托=5尺。 解法1二元一次方程组 设索长为x托,竹竿长为y托,则 x-y=1 (6-1) 1 y-2x=1 (6-2) 竿索 (6-1)+(6-2)得 x=2 x=4 继续上升 所以 y=3 即索长4托=2丈,竿长3托=1 丈5尺。 解法2图示法 1托 画一个简图,用心算(如图 61)。先将绳索超出竹竿的部分折回 托 并继续上升,注意上升的高度是下面 图6-1 绳索比竹竿缩短的部分的2倍,即上 22