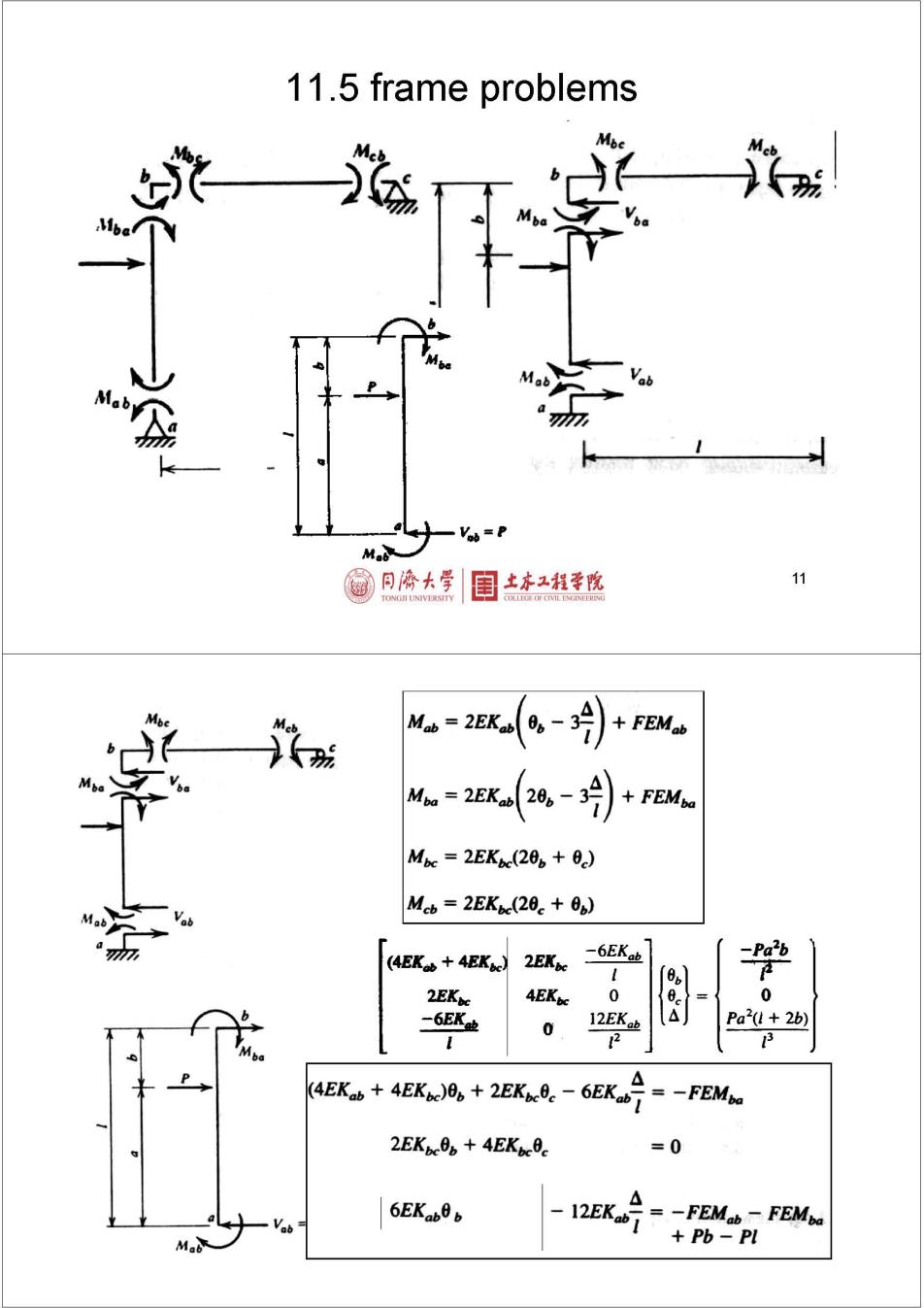
11.5 frame problems 一V= 同停大学 目 土床工程学院 11 FEMab Mba 2EKab 20。-3号》 FEM Mc=2EKbc(20。+0.) Meb 2EKbe(20c+0g) (EK+4EKc) 2EKpe -6EKab -Pa2b 2EKbe 4EKbc 0 0 -6EK业 0 12EKab Pa"(l 2b) 2 下 4EK+EK)+2EK-EK =-FEMbe 2EK0+4EKbc0c =0 6EKab0 -12EKab =-FEMab FEMba Ma Pb-Pl

Procedure of the slope deflection method The displacement boundary conditions A qualitative sketch of the deflected structure The compatibility requirements The unknown displacement quantities A slope deflection equation for each member end A rotational freedom involving the An equilibrium equation for moments acting on the joint each kinematic dof A sway freedom involving column shears and moments The equilibrium equations in terms of unknown displ. Determination of the unknown displacements End moments coming from the slope deflection equation 同榜大学 土本工程学院 13 Example 11.2 Determine the end moments and the maximum bending stress for the structure below,if point b settles 0.03m. E=200×10Pa=200GN/m2:1=2000×10-6m:d=0.3 m(beam depth) 0.03m b ab=0.03/10=0.003 c=-0.003 Compatibility and Boundary Conditions 0 and 0 are the two kinematic degrees of freedom. Moment Equations M=2EK(20+0-3)+FEM Kb=K=K=200X10-6m=200×10-7m 10m EK=200GN× m×200×107m3=40MN.m 14
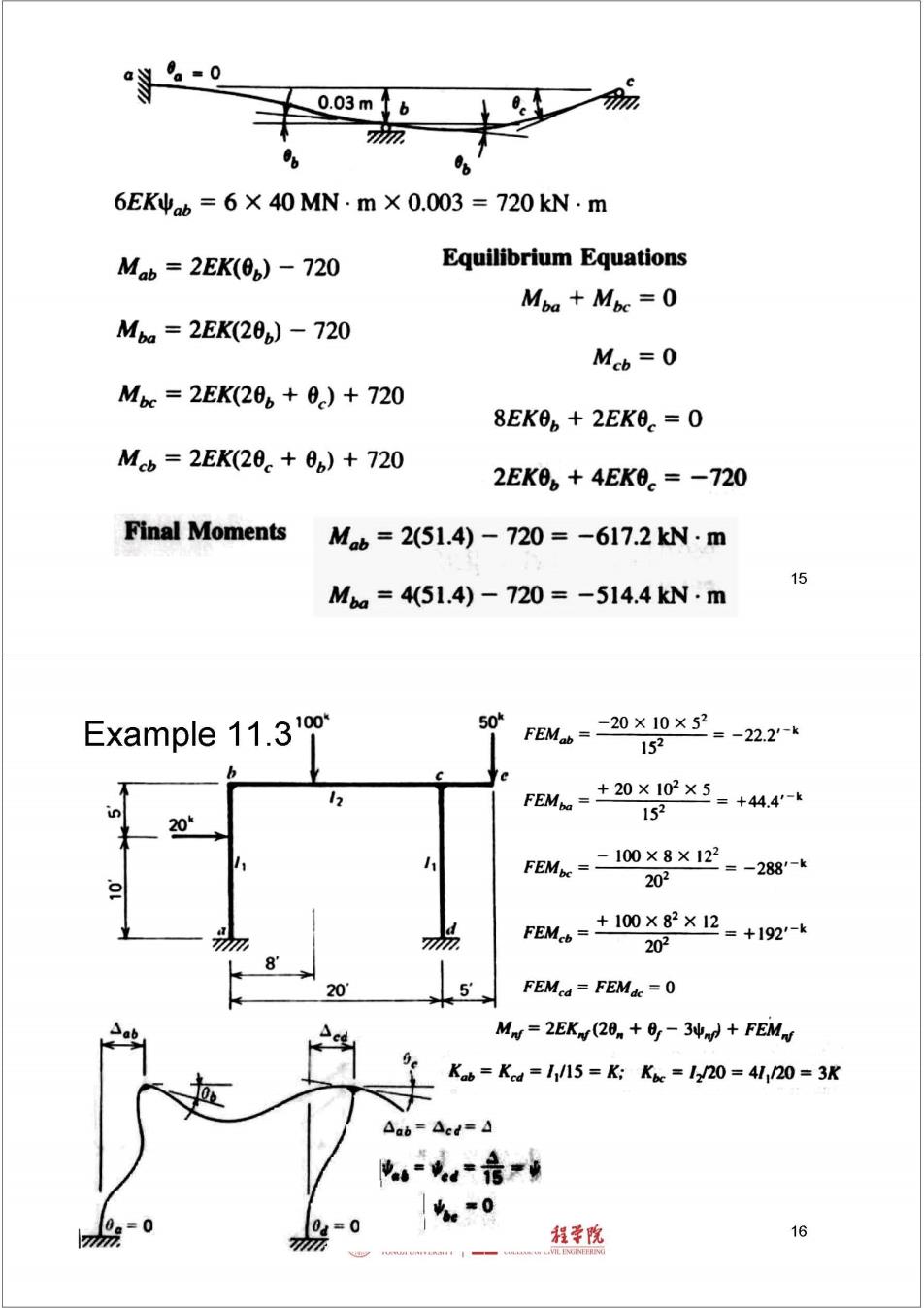
议 =0 0.03m 6EKψab=6×40MN.m×0.003=720kN.m Mb=2EK(0b)-720 Equilibrium Equations Mba Mic =0 Mba=2EK(20b)-720 Mcb=0 Mbc=2EK(20b+0)+720 8EK0b+2EK0。=0 Mb=2EK(20。+0b)+720 2EK0。+4EK0.=-720 Final Moments Mb=2(51.4)-720=-617.2kN·m 15 Ma=451.4)-720=-514.4kN.m Example 11.310 50 FEMb=-20X10×52 =-22.2'-k 152 FEM=+20X02×5-+444-t n 20 152 FBM=二10X8X12=-288-+ 202 FEMb=+10×82X2=+192-k 202 81 5 FEMed=FEMdc=0 My=2EKy (20+0-3+FEM Kab=Kod =1/15=K;Kic 12/20=41 120=3K △ab=4cd=4 u或6=音产号 鼎0 90 吃e=0 程学脱 16

100 50 Me=-(50×5)=-250'-k (from statics) Mab=2EK(0。-3)-22.2 20 Ma=2EK(20。-3)+44.4 M=2E·3K(20b+0)-288 汤 n 8 20 5 Mb=2E·3K(20e+6b)+192 Mcd=2EK(20。-3ψ) Equilibrium Equations Mk=2EK(0e-3ψ) At joint b: Msa Moc =0 250h At joint c: M+M-250=0 学院 17 Columns ab and cd: 5 204 10 一H Mab M from consideration of the entire structure, H。+Ha=20 .'.Mab Mpe Mca+Mac =-200 Substitution of moment equations into the equilibrium equations yields 6 -61EK06l [243.6 6 16 EKO。 58.0 -6 24 EK业 222.2 18