
例3:用变量y表示水稻产量,若y大于500kg的概率 为0.25,大于300kg且等于小于500kg的概率为0.65,等 于小于300kg的概率为0.1。 则用变量y的取值范围来表示的试验结果为 Pys300)=0.10, P300<ys500)=0.65, Py>500)=0.25
例3:用变量y表示水稻产量,若y大于500kg的概率 为0.25,大于300kg且等于小于500kg的概率为0.65,等 于小于300kg的概率为0.1。 则用变量y的取值范围来表示的试验结果为 P(y≤300)=0.10, P(300<y≤500)=0.65, P(y>500)=0.25

离散型随机变量-当试验只有几个确定的结果,并可一 一列出,变量y的取值可用实数表示,且y取某一值时,其概率 是确定的,这种类型的变量称为离散型随机变量。 将这种变量的所有可能取值及其对应概率一一列出所形成 的分布称为离散型随机变量的概率分布: 变量y: y1 '2 y3 yn 概率P(y=y,)P1P2 P3 Pn P(y=y,)也可用函数f)表述,称为概率函数
离散型随机变量 -当试验只有几个确定的结果,并可一 一列出,变量y的取值可用实数表示,且y取某一值时,其概率 是确定的,这种类型的变量称为离散型随机变量。 将这种变量的所有可能取值及其对应概率一一列出所形成 的分布称为离散型随机变量的概率分布: 概率 P(y = yi ) 变量yi y1 y2 y3 . yn P1 P2 P3 . Pn P(y = yi ) 也可用函数f(y)表述,称为概率函数
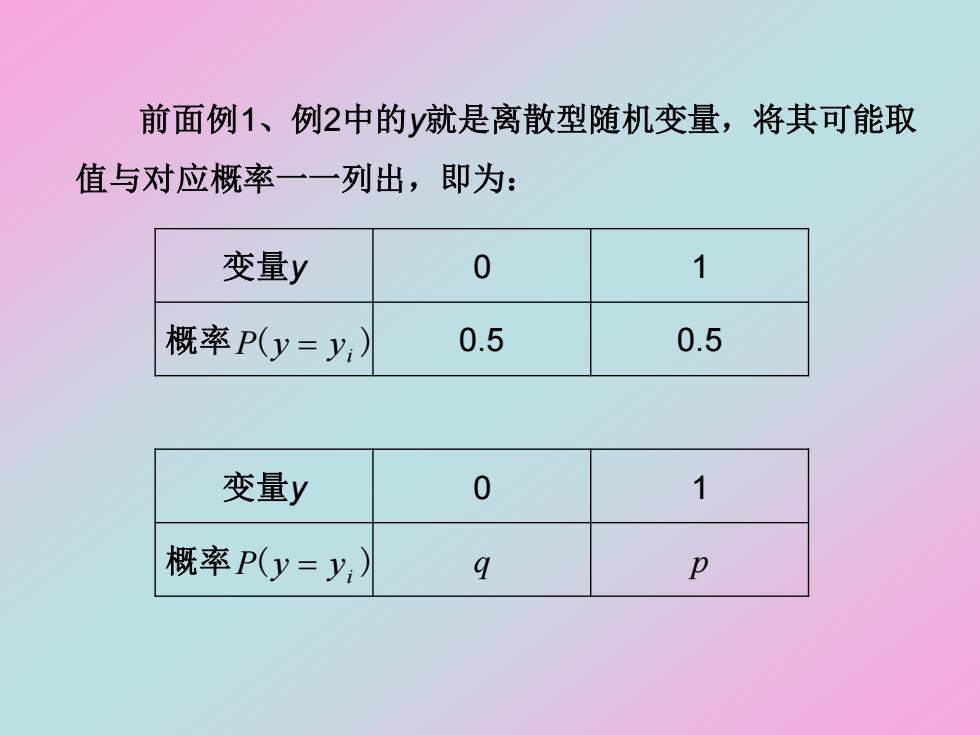
前面例1、例2中的y就是离散型随机变量,将其可能取 值与对应概率一一列出,即为: 变量y 0 1 概率P(y=y 0.5 0.5 变量y 0 1 概率Py=y,) q 卫
前面例1、例2中的y就是离散型随机变量,将其可能取 值与对应概率一一列出,即为: 变量y 0 1 概率 ( ) 0.5 0.5 i P y = y 变量y 0 1 概率 ( ) q p i P y = y

连续型随机变量(continuous random variate))-对于随 机变量,若存在非负可积函数y(-o<y<十∞),对任 意a和b(a<b)都有P(asy<b)Ff(y)d则称y为连续 型随机变量(continuous random variate),fy)称为y的概率密 度函数(probability density function)或分布密度(distribution density)。 上述例3中的y就是一个连续型随机变量
连续型随机变量(continuous random variate) -对于随 机变量,若存在非负可积函数f(y)(-∞<y<+∞),对任 意a和b(a<b)都有P(a≤y<b)= ,则称y为连续 型随机变量(continuous random variate),f(y)称为y的概率密 度函数(probability density function)或分布密度(distribution density)。 b a f ( y)dy 上述例3中的y就是一个连续型随机变量

第二节二项式分布 一、二项总体及二项式分布 二、二项式分布的概率计算方法 三、二项式分布的形状和参数 四、多项式分布
第二节 二项式分布 一、二项总体及二项式分布 二、二项式分布的概率计算方法 三、二项式分布的形状和参数 四、多项式分布