
内蒙古农业大学食品科学与工程学院《食品工程原理》讲稿 CH5-§2 表 5-3 气体的导热系数 Thermal conductivity for gases 气体 温度,℃ 导热系数,λ W/m·K 氢 0 0.17 二氧化碳 0 0.015 空气 0 0.024 空气 100 0.031 甲烷 0 0.029 水蒸汽 100 0.025 氮 0 0.024 乙烯 0 0.017 氧 0 0.024 乙烷 0 0.018 5—3 通过平壁的稳定热传导 Steady Heat Conduction through slab 5.3A 单层平壁的稳定热传导 Heat Transfer Through a slab 下面讨论单层平壁稳定热传导的导热速率计算。 6
内蒙古农业大学食品科学与工程学院《食品工程原理》讲稿 CH5-§2 表 5-3 气体的导热系数 Thermal conductivity for gases 气体 温度,℃ 导热系数,λ W/m·K 氢 0 0.17 二氧化碳 0 0.015 空气 0 0.024 空气 100 0.031 甲烷 0 0.029 水蒸汽 100 0.025 氮 0 0.024 乙烯 0 0.017 氧 0 0.024 乙烷 0 0.018 5—3 通过平壁的稳定热传导 Steady Heat Conduction through slab 5.3A 单层平壁的稳定热传导 Heat Transfer Through a slab 下面讨论单层平壁稳定热传导的导热速率计算。 6

内蒙古农业大学食品科学与工程学院《食品工程原理》讲稿 CH5-§2 图所示为一平壁。壁厚为 b,壁的面积为 A,假定壁的材质均匀, 导热系数λ不随温度变化,视为常数,平壁的温度只沿着垂直于壁面 的 x 轴方向变化,故等温面皆为垂直于 x 轴的平行平面。若平壁侧面 的温度 T1及 T2恒定,则当 x=0 时,T= T1;x=b 时,T= T2,根据傅立 叶定律 ( ) ∫ ∫⋅ ⋅ Φ = − Φ Φ = − ⋅ ⋅ T b T dx A dt For dx dT A 0 2 1 the Staedy Heat Transfer, is a constant. 5 - -15 λ λ 分离变量后积分: 式(4-9)可写为 ( ) R T b T T T T A b q ∆ = − = ⋅ − = Φ= λ λ 1 2 1 2 ( 5-16) For the slab that has a area of A, A b T q A λ ∆ Φ = ⋅ = (5—17) 式(4-10)中ΔT = T1-T2 为导热的推动力(driving force),而 A b R λ = 则为导热的热阻(thermal resistance)。 例 4-2 现有一厚度为 240mm 的砖壁,内壁温度为 600℃,外壁 温度为 150℃。试求通过每平方米砖壁的热量。已知该温度范围内砖 7
内蒙古农业大学食品科学与工程学院《食品工程原理》讲稿 CH5-§2 图所示为一平壁。壁厚为 b,壁的面积为 A,假定壁的材质均匀, 导热系数λ不随温度变化,视为常数,平壁的温度只沿着垂直于壁面 的 x 轴方向变化,故等温面皆为垂直于 x 轴的平行平面。若平壁侧面 的温度 T1及 T2恒定,则当 x=0 时,T= T1;x=b 时,T= T2,根据傅立 叶定律 ( ) ∫ ∫⋅ ⋅ Φ = − Φ Φ = − ⋅ ⋅ T b T dx A dt For dx dT A 0 2 1 the Staedy Heat Transfer, is a constant. 5 - -15 λ λ 分离变量后积分: 式(4-9)可写为 ( ) R T b T T T T A b q ∆ = − = ⋅ − = Φ= λ λ 1 2 1 2 ( 5-16) For the slab that has a area of A, A b T q A λ ∆ Φ = ⋅ = (5—17) 式(4-10)中ΔT = T1-T2 为导热的推动力(driving force),而 A b R λ = 则为导热的热阻(thermal resistance)。 例 4-2 现有一厚度为 240mm 的砖壁,内壁温度为 600℃,外壁 温度为 150℃。试求通过每平方米砖壁的热量。已知该温度范围内砖 7

内蒙古农业大学食品科学与工程学院《食品工程原理》讲稿 CH5-§2 壁的平均导热系数λ=0.6W/m·℃。 解 ( ) 2 1 2 1125W/m 0.60/0.24 (600 -150) = = × q = Φ A = λ b T − T 5.3B 多层平壁的稳定热传导 The Steady Heat Transfer through composite slab 今以图所示的三层平壁为例,讨论多层平壁的稳定热传导问题。 假定各层壁的厚度分别为 b1,b2,b3,各层材质均匀,导热系数分别 为λ1,λ2,λ3,皆视为常数,层与层之间接触良好,相互接触的表 面上温度相等,各等温面亦皆为垂直于 x 轴的平行平面。壁的面积为 A,在稳定导热过程中,穿过各层的热量必相等。与单层平壁同样处 理,可得下列方程。 8
内蒙古农业大学食品科学与工程学院《食品工程原理》讲稿 CH5-§2 壁的平均导热系数λ=0.6W/m·℃。 解 ( ) 2 1 2 1125W/m 0.60/0.24 (600 -150) = = × q = Φ A = λ b T − T 5.3B 多层平壁的稳定热传导 The Steady Heat Transfer through composite slab 今以图所示的三层平壁为例,讨论多层平壁的稳定热传导问题。 假定各层壁的厚度分别为 b1,b2,b3,各层材质均匀,导热系数分别 为λ1,λ2,λ3,皆视为常数,层与层之间接触良好,相互接触的表 面上温度相等,各等温面亦皆为垂直于 x 轴的平行平面。壁的面积为 A,在稳定导热过程中,穿过各层的热量必相等。与单层平壁同样处 理,可得下列方程。 8

内蒙古农业大学食品科学与工程学院《食品工程原理》讲稿 CH5-§2 第一层 1 2 1 1 1 1 1 1 2 1 1 t t t A b b t t A Φ = − = ∆ − Φ = λ λ 同理,第二层 2 2 2 2 t A b Φ = ∆ λ 第三层 3 3 3 3 t A b Φ = ∆ λ 对于稳定导热过程: Φ = Φ = Φ = Φ (5—18) 1 2 3 1 2 3 3 3 2 2 1 1 t t t A b A b A b = ∆ + ∆ + ∆ Φ + + λ λ λ 此 应用合比定理(merge proportion law),式(5-18)亦可写成下 面形式 1 2 3 1 4 1 2 3 1 2 3 R R R t t R R R t t t + + − = + + ∆ + ∆ + ∆ Φ = (5—19) 同理,对具有 n 层的平壁,穿过各层热量的一般公式为 ∑ − + = Φ= n i i n b t t A q 1 1 1 λ (5-20) 式中 i 为 n 层平壁的壁层序号。 9
内蒙古农业大学食品科学与工程学院《食品工程原理》讲稿 CH5-§2 第一层 1 2 1 1 1 1 1 1 2 1 1 t t t A b b t t A Φ = − = ∆ − Φ = λ λ 同理,第二层 2 2 2 2 t A b Φ = ∆ λ 第三层 3 3 3 3 t A b Φ = ∆ λ 对于稳定导热过程: Φ = Φ = Φ = Φ (5—18) 1 2 3 1 2 3 3 3 2 2 1 1 t t t A b A b A b = ∆ + ∆ + ∆ Φ + + λ λ λ 此 应用合比定理(merge proportion law),式(5-18)亦可写成下 面形式 1 2 3 1 4 1 2 3 1 2 3 R R R t t R R R t t t + + − = + + ∆ + ∆ + ∆ Φ = (5—19) 同理,对具有 n 层的平壁,穿过各层热量的一般公式为 ∑ − + = Φ= n i i n b t t A q 1 1 1 λ (5-20) 式中 i 为 n 层平壁的壁层序号。 9
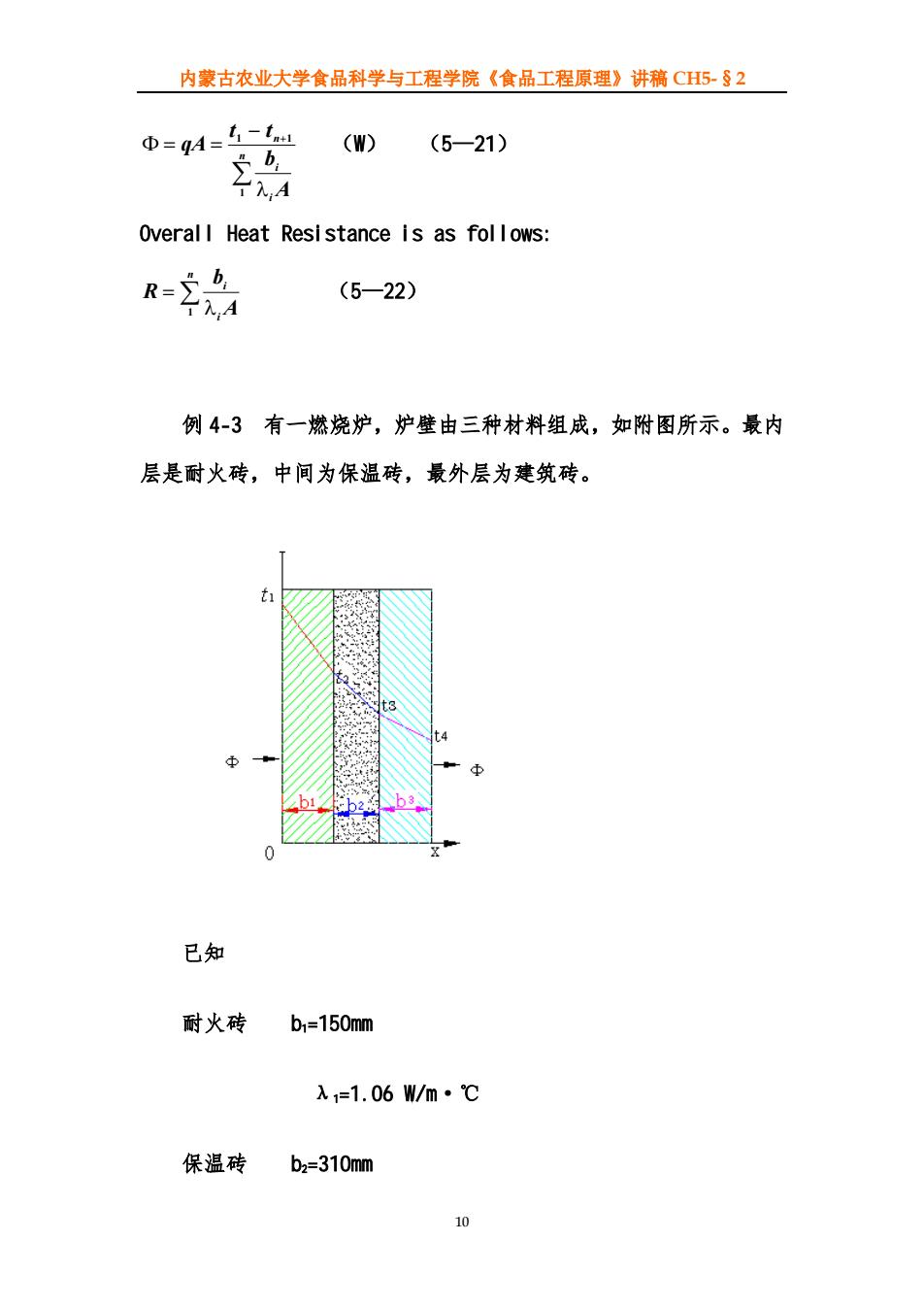
内蒙古农业大学食品科学与工程学院《食品工程原理》讲稿 CH5-§2 ∑ − + Φ = = n i i n A b t t qA 1 1 1 λ (W) (5—21) Overall Heat Resistance is as follows: = ∑ n i i A b R 1 λ (5—22) 例 4-3 有一燃烧炉,炉壁由三种材料组成,如附图所示。最内 层是耐火砖,中间为保温砖,最外层为建筑砖。 已知 耐火砖 b1=150mm λ1=1.06 W/m·℃ 保温砖 b2=310mm 10
内蒙古农业大学食品科学与工程学院《食品工程原理》讲稿 CH5-§2 ∑ − + Φ = = n i i n A b t t qA 1 1 1 λ (W) (5—21) Overall Heat Resistance is as follows: = ∑ n i i A b R 1 λ (5—22) 例 4-3 有一燃烧炉,炉壁由三种材料组成,如附图所示。最内 层是耐火砖,中间为保温砖,最外层为建筑砖。 已知 耐火砖 b1=150mm λ1=1.06 W/m·℃ 保温砖 b2=310mm 10