第二章逻辑代数和函数化简 五、波形图 输入变量和对应的输出变量随 时间变化的波形 B Y=AB Y 优点:形象直观地表示了变量取值与函数值在时间上 的对应关系。 缺点:难以用公式和定理进行运算和变换,当变量个 数增多时,画图较麻烦
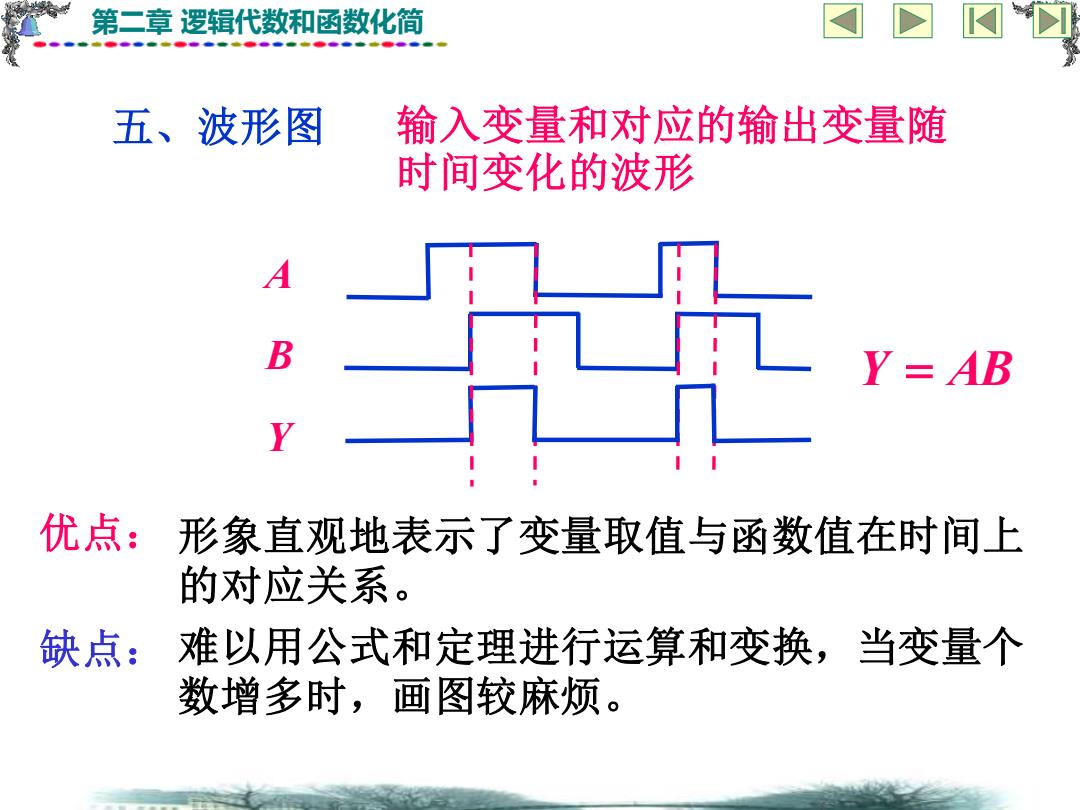
第二章 逻辑代数和函数化简 五、波形图 输入变量和对应的输出变量随 时间变化的波形 Y = AB A B Y 优点: 形象直观地表示了变量取值与函数值在时间上 的对应关系。 缺点: 难以用公式和定理进行运算和变换,当变量个 数增多时,画图较麻烦
第二章逻辑代数和函数化简 2.2.3逻辑函数各种表示方法间的相互转换 一、真值表→「 函数式→逻辑图 [例]设计一个举重裁判电路。在一名主裁判(A) 和两名副裁判(B、C)中,必须有两人以上(必有主 裁判)认定运动员的动作合格,试 B 举才算成功。 U U (1)真值表→ 函数式 U 将真值表中使逻辑函数Y=1的 0 输入变量取值组合所对应的最小项相 C......cnecacsonconeconec. 指每每■ ■男男■■■■g■■■g■■g8 加,即得Y的逻辑函数式。 国海国国国海国细细国细等 国海国 Y=ABC+ABC+ABC 想里目8组8目8 面■量相面童■指面■面量■量相国 是n目8组指B8图
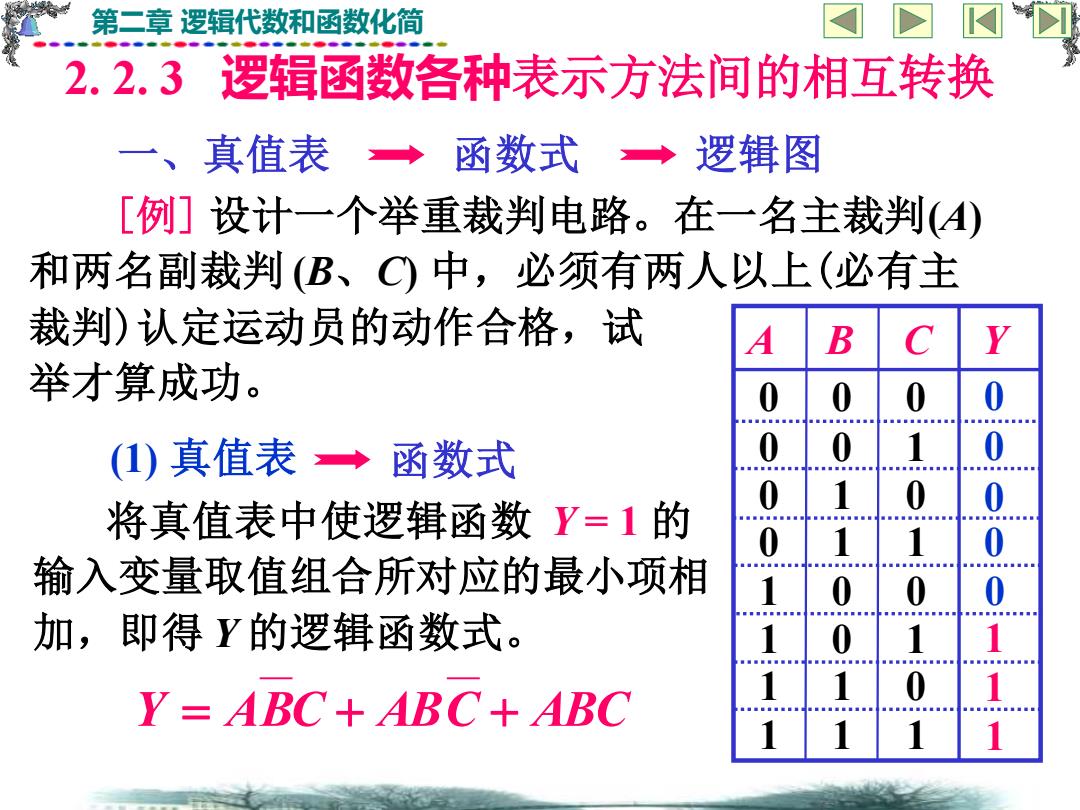
第二章 逻辑代数和函数化简 2. 2. 3 逻辑函数各种表示方法间的相互转换 一、真值表 函数式 逻辑图 [例] 设计一个举重裁判电路。在一名主裁判(A) 和两名副裁判 (B、C) 中,必须有两人以上(必有主 裁判)认定运动员的动作合格,试 举才算成功。 (1) 真值表 函数式 Y = ABC + ABC + ABC 将真值表中使逻辑函数 Y = 1 的 输入变量取值组合所对应的最小项相 加,即得 Y 的逻辑函数式。 A B C Y 0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1 0 0 0 0 0 1 1 1
第二章逻辑代数和函数化简 函数式 Y=ABC+ABC+ABC BC 卡诺图化简 A 00011110 Y-AB+AC 0 0 0 0 0 111 (2)函数式→逻辑图 A & B Y &
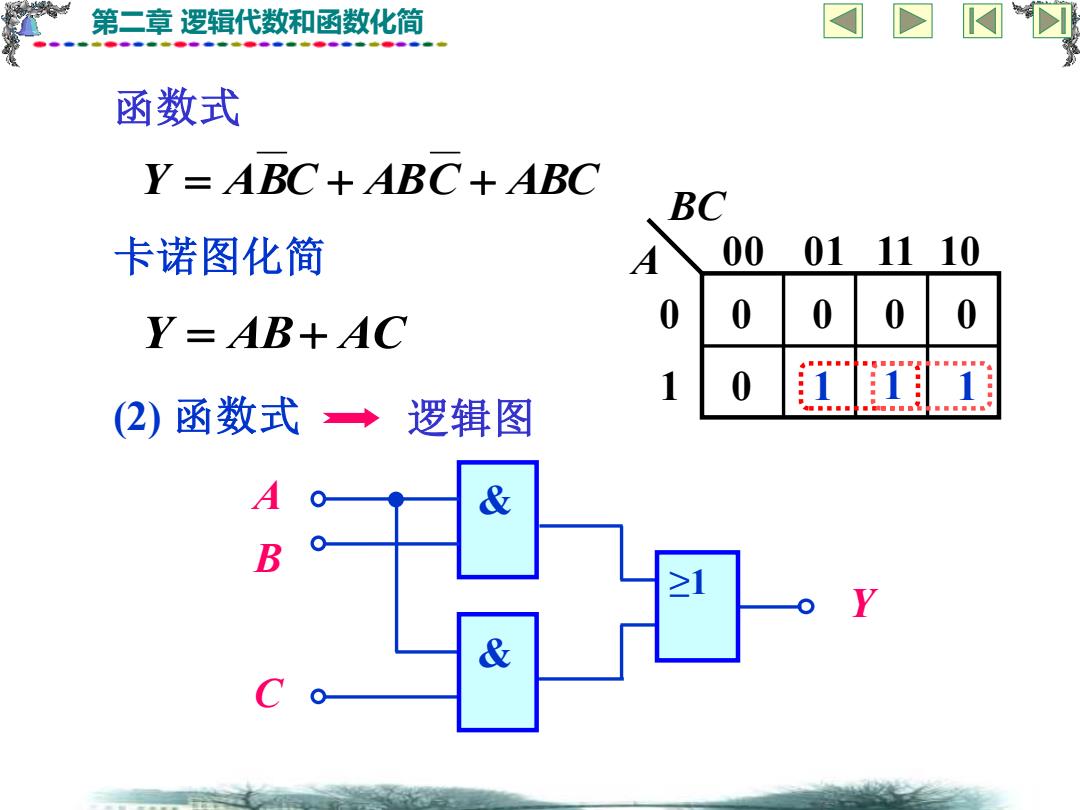
第二章 逻辑代数和函数化简 函数式 Y = ABC + ABC + ABC 卡诺图化简 A BC 0 1 00 01 11 10 1 1 0 1 0 0 0 0 Y = AB+ AC (2) 函数式 逻辑图 A B Y & C & ≥1
第二章逻辑代数和函数化简 二、逻辑图 →函数式→真值表 & A·AB & & & Y=A·AB.B.AB B·AB B =A.AB+B.AB =A(A+B)+B(A+B) A B Y 0 0 0 =AB+AB 0 1 =A⊕B U ... 1
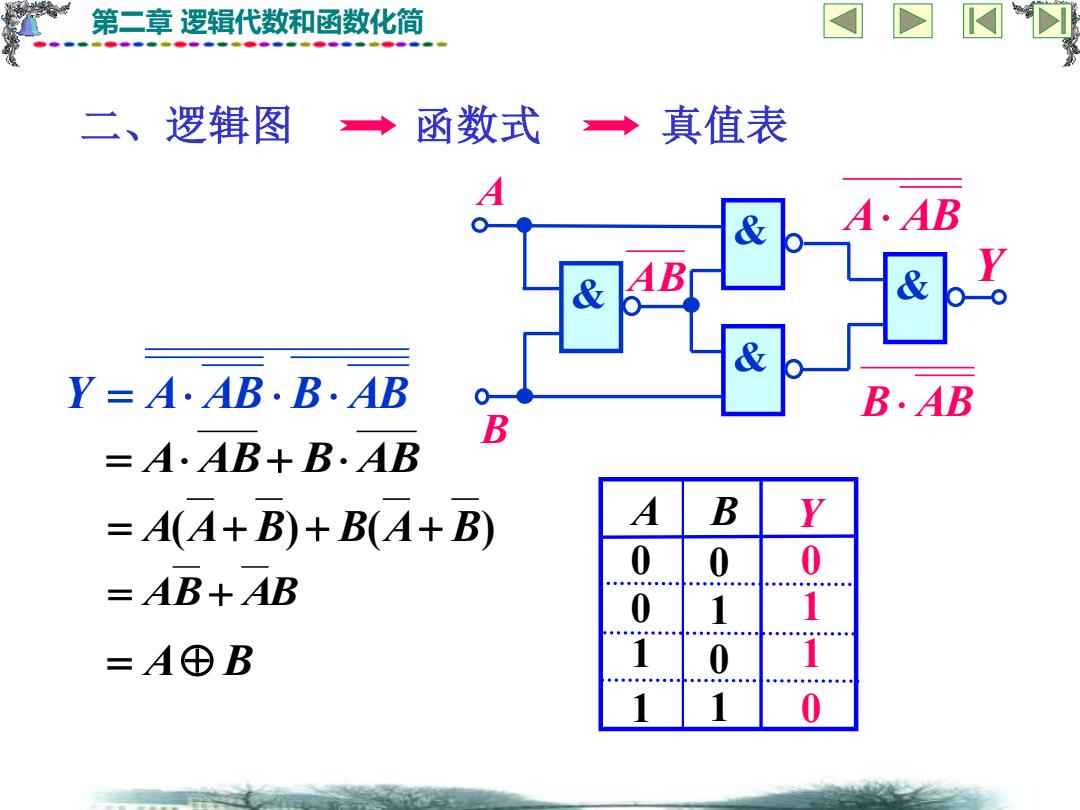
第二章 逻辑代数和函数化简 二、逻辑图 函数式 真值表 Y = A AB B AB = A AB+ B AB = A(A+ B)+ B(A+ B) = AB+ AB = A B 0 1 1 0 A B Y 0 0 0 1 1 0 1 1 AB A AB B AB B A Y & & & &

第二章逻辑代数和函数化简 2.3逻辑代数的运算法则 2.3.1逻辑函数的相等 F=(a,a2,...an) F=f2(a1,a2,.an) 若两逻辑函数具有相同的真值表, 则这两个逻辑函数相等
第二章 逻辑代数和函数化简 2.3 逻辑代数的运算法则 2.3.1 逻辑函数的相等 ( , ,... ) ( , ,... ) 2 2 1 2 1 1 1 2 n n F f a a a F f a a a = = 若两逻辑函数具有相同的真值表, 则这两个逻辑函数相等