
3.4典型数控功能原理及实现 第二步精插补: 数控装置通过检测装置定时对实际位移采样,根据采 样周期T的大小,采用直线的基准脉冲插补,在轮廓步 长内插入若干点。 插补采样周期T0与位置采样周期T的关系:T0=nT 在粗插补算出的每一微小直线段的基础上再作“数据点 的密化”工作。 一般将粗插补运算称为插补,由软件完成;精插补可由 软件、硬件实现。 21
21 第二步精插补: 数控装置通过检测装置定时对实际位移采样,根据采 样周期T的大小,采用直线的基准脉冲插补,在轮廓步 长内插入若干点。 插补采样周期T0与位置采样周期T的关系:T0=n T反馈 在粗插补算出的每一微小直线段的基础上再作“数据点 的密化”工作。 一般将粗插补运算称为插补,由软件完成;精插补可由 软件、硬件实现。 3.4 典型数控功能原理及实现

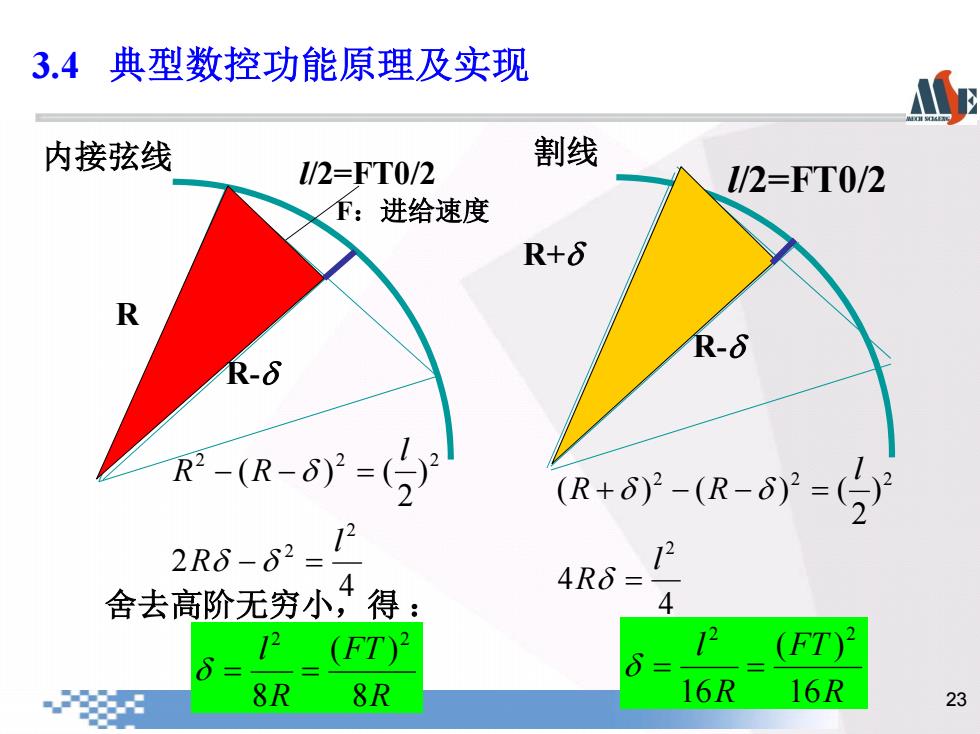
3.4典型数控功能原理及实现 如何计算各坐标轴的增量△x或△y: 前一插补周期末端点坐标值 本次插补周期内坐标增量值 → 计算出本次插补周期末端点位置坐标值。 对直线插补,不会造成轨迹误差。 对圆弧插补,将轮廓步长作为内接弦线或割线来逼近圆 弧,会带来轮廓误差。 22
22 如何计算各坐标轴的增量△x或△y: 前一插补周期末端点坐标值 本次插补周期内坐标增量值 计算出本次插补周期末端点位置坐标值。 对直线插补,不会造成轨迹误差。 对圆弧插补,将轮廓步长作为内接弦线或割线来逼近圆 弧,会带来轮廓误差。 3.4 典型数控功能原理及实现
3.4典型数控功能原理及实现 内接弦线 L/2=FT0/2 割线 L/2=FT0/2 了:进给速度 R+8 R f-6 f-6 R2-(R-2=(5 (R+2-(R-6=( 2R6-d2=1 舍去高阶无穷小,4 得: 4R=12 4 12 (FT)2 12 (FT)2 8R 8R 16R 16R 23
23 4 2 ) 2 ( ) ( 2 2 2 2 2 l R l R R 舍去高阶无穷小,得 : R FT R l 8 ( ) 8 2 2 4 4 ) 2 ( ) ( ) ( 2 2 2 2 l R l R R R FT R l 16 ( ) 16 2 2 内接弦线 R l/2=FT0/2 R- R- R+ l/2=FT0/2 割线 F:进给速度 3.4 典型数控功能原理及实现

3.4典型数控功能原理及实现 割线逼近时计算复杂,应用较少。 δ<1个脉冲当量,所以:F、R一定时,T0越短,6越小。 插补周期应尽量选得小一些。 当6、T0确定后,根据R选择F,保证6不超过允许值。 24
24 割线逼近时计算复杂,应用较少。 <1个脉冲当量,所以:F、R一定时,T0越短, 越小。 插补周期应尽量选得小一些。 当 、T0确定后,根据R选择F,保证 不超过允许值。 3.4 典型数控功能原理及实现

3.4典型数控功能原理及实现 闭环、半闭环系统采用数据采样插补方法: 粗插补:每一T0内计算出指令位置增量; 精插补:每一T反馈实际位置增量值及指令位置增量值;算出 跟随误差,再算出相应坐标轴进给速度,输出给驱动装置。 数据采样插补方法很多:直线函数法、扩展数字积分法、二阶 递归扩展数字积分法、双数字积分插补法等。 25
25 闭环、半闭环系统采用数据采样插补方法: 粗插补:每一T0内计算出指令位置增量; 精插补:每一T反馈实际位置增量值及指令位置增量值;算出 跟随误差,再算出相应坐标轴进给速度,输出给驱动装置。 数据采样插补方法很多:直线函数法、扩展数字积分法、二阶 递归扩展数字积分法、双数字积分插补法等。 3.4 典型数控功能原理及实现