
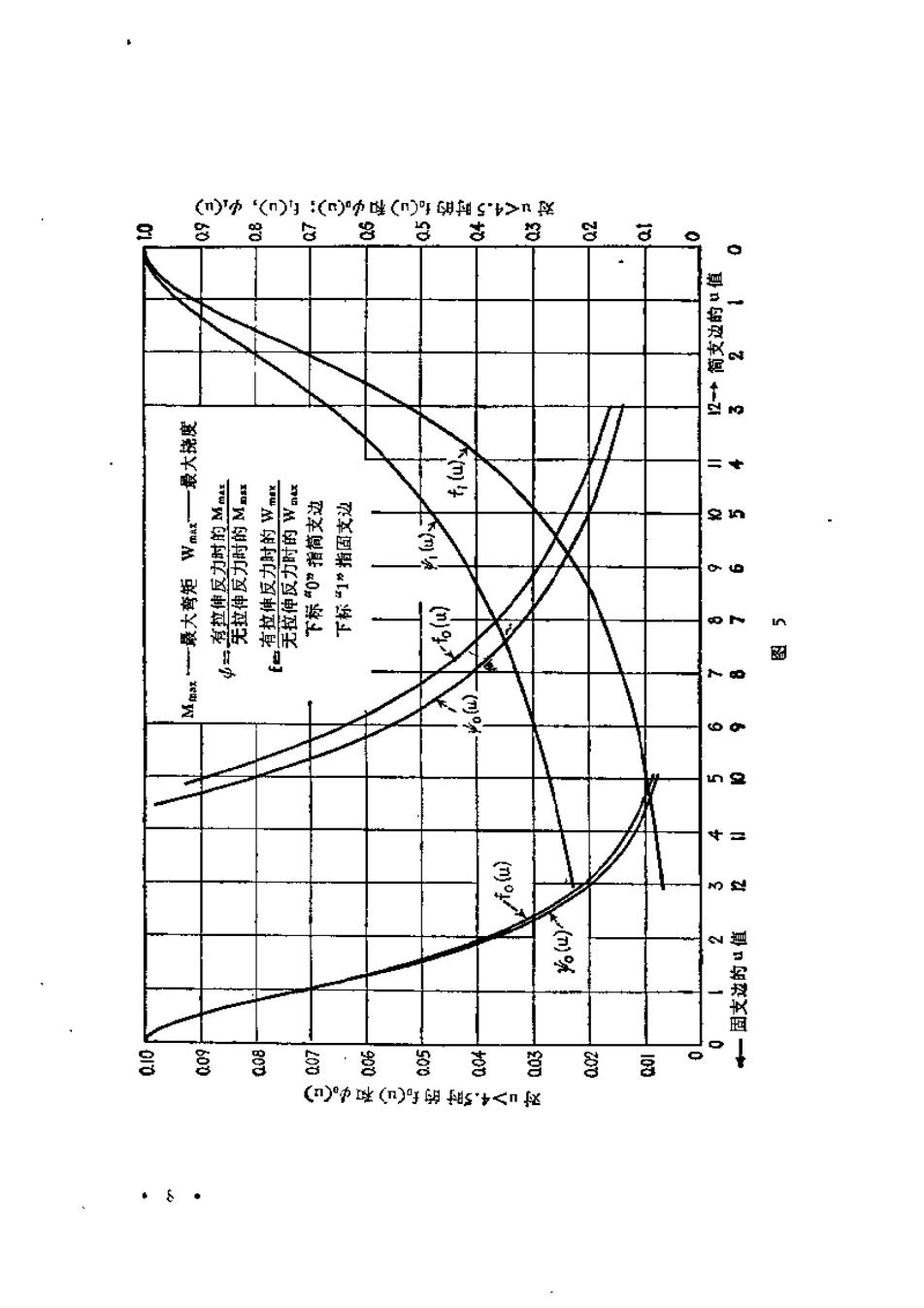
多 引入因子10*是为了使对数值为正:.在每一个别情况下,先计算 方程(8)左端的平方根,也即F/(1一y)g,它给出√U。.数 值log(1GV√U。)给出图4的纵坐标,从而由曲线容易地得出柑 应的4值.已知4值,轴向力S即可由式(5)求得. 在计算应力时,我们]注意到在单元条的任何横截面上,它的总 应力由弯曲应力和拉应力组成.此弯曲应力与弯矩成正比,而拉 应力的值S/h沿条长为常数最大应力发生在单元条的中间,因为 间的弯矩最大。由微分方程(4)得最大弯矩为 Mmix =-D 代人(6)式的w值,则得 Mn=h,(), (9) 8 式中 中。✉1-sch (e) 2 中的数值由图5的由线给出。显然,当俏增加时,这些数值很 快地减小,并且当为大值时,最大弯比单元条二端没有拉仲反 力时的弯矩g严/8小了好儿倍. 现在,拉伸应力,和最大弯曲应力5:可以容易用,g和板 的常数表示为 (10) (11) 而板中的最大应力为 0max=01十02. 为了说明如何运用图4和图5的曲线来计算最大应力,可举一个 数字例子;即取-一长矩形板,宽为130里米厚为13毫米,并设有匀 匀载荷9=1.4公了/厘米2(E=2.1×10公斤/厘米).今先计 ·7
(中(n)y:()°中唑(n)ysb>ng 8 3 吉 8 8 言 象1n 留 是 三 罩 含·堂 g 莒 曾 莒 哥 ()中唑(n)呼明sb<n这

算√U,: atess. 由对数表可知 1ogo(10*VU0)=2.217. 由图4的曲线A得到t=3.795,并由图5得到中o=0329. 现在用式(10)和(11)计算应力,即得 ,=2.1×10×37951=1108公斤/厘米, 3(1-0.32) 104 ·2-3×1.4×101×0.1329=1395公斤/厘米2, 0max=0,+2=2503公斤/厘米2. 在计算最大挠度时,可将x一/2代入挠度曲线方程(6),这样便 得到 m), (12) 384D 式中 sech u-1+ fo(u)= 2 5u 24 为了简化计算,用图5的曲线表示f(w)的数值.假在单元条 的二端无拉伸反力,则最大挠度就会是5g/384D.此拉伸反力 的影响可用因子()表示。当“增加时,这因子的数值即迅速 减小, 如把图5用到前所讨论的数字例子中,则知当#=3.795时, f(4)的值为0.145.将此值代入式(12),即得 wmax=I2X0.145≈1.74厘米」 由方程(8)可1,当板的材料给定时,表示拉伸的参数“决定 于载荷4的强度和板宽与板厚之比1/h.由式(10)和(11)则知应 力σ,与o2也是,4和/h的函数.所以板中的最大应力仅决定

于载可?利比俏1h.这说明作出-一簇用载荷?表示最大应力 为曲线.每一曲线对应着一个值.这样的曲线给在图6中. 由于拉力S的出现,并月它随裁荷的增面增加,可知最大应力不 与裁荷9成正比.当9为大俏,最大应力在板草变化时变化不大 取标明/一100的曲线,并设9=1.4公斤/厘米2,则由曲线可 得上述数宁例子第出的omx行. 4000 简支钢板的应力 h=220 3000 =200 8 名品 2000 1000 1一咒与厚之比 0.5 1.0 1.5 2.0 2.3 2.8 载蔺(公行/厘米) 图6 3.承受均匀载荷的固支矩形板的柱形弯曲 假设板的长边 被固定使它不能旋转.仍如以前图1的作法,取一单位完的单元 条.用M表示板的长边每单位长度上所受的弯矩,作用在这 条上的力如图7所示.在单元条的任一横戴面上的弯矩为: M9x-9x-Sw Mos 3 2 将此式代入方程(4)则财得: dxi (a) D 2D 2D D 。0
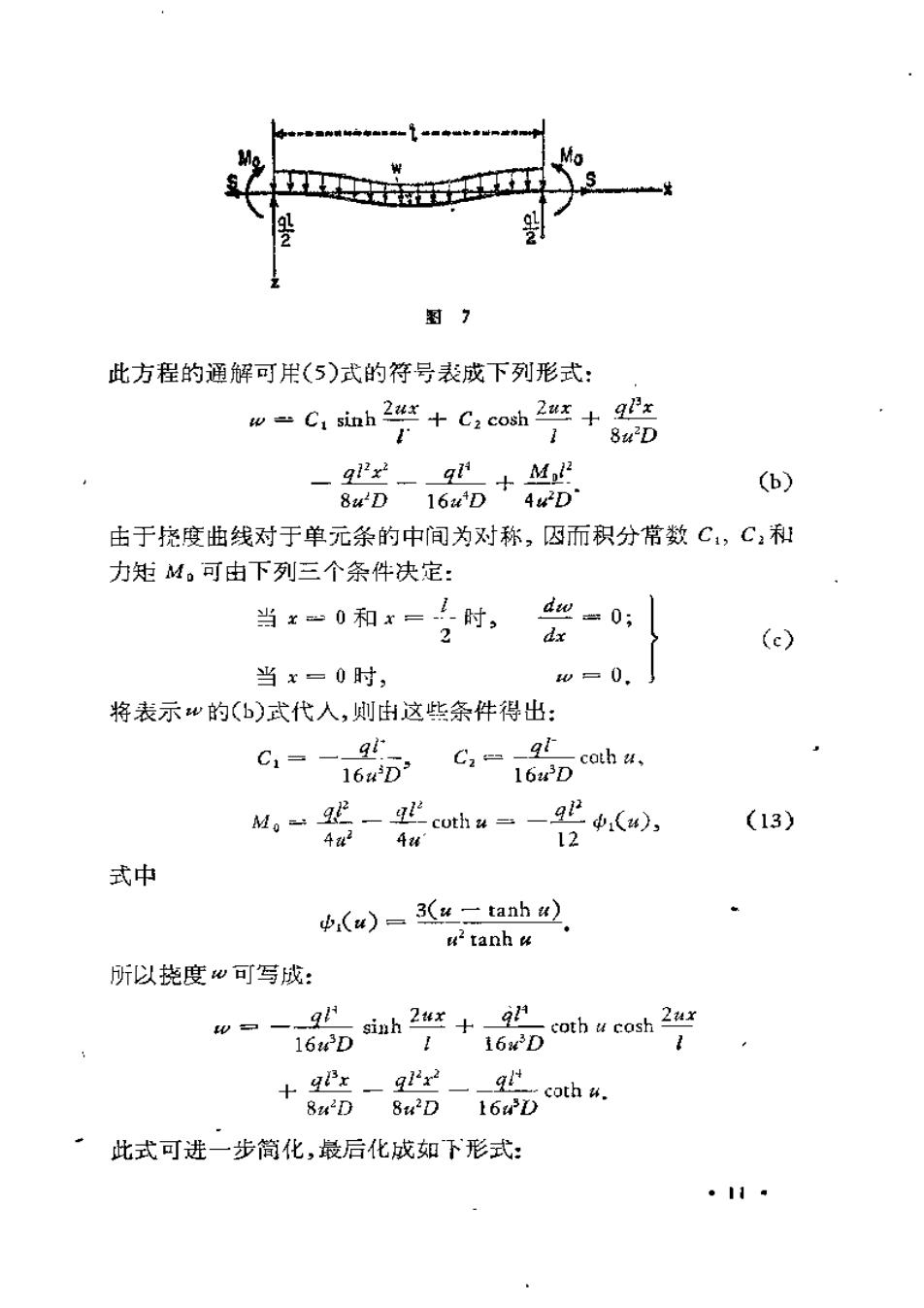
Mo 图7 此方程的通解可用(5)式的符号表成下列形式: wCI sinh +C:coshux 8uD 9x2914 +42 16uD 4uD (6) 8u'D 由于挠度曲线对于单元条的中间为对称,囚而积分常数C1,C,和 力矩M。可由下列三个条件决定: 当x一0和x=时, d=0 2 dx (c) 当x=0时, w=0. 将表示w的(b)式代人,则由这些条件得出: C1=一9 C2=-9 coth # 164D1 16x3D M。一一gcoh4=-9 中(4), (13) 4424w 12 式中 中,(w)=3(一tanh) 4tanh 所以挠度w可写成: w一一 9 simhu coth u cosh 2u 16uD 116e3D +4-9-9coh4. 8uD 8u2D16w3 ·此式可进一步简化,最后化成如下形式: