
例 图示电路,i1=10A,i=5c0s(10t),L=2H,L2=3H, M=1H,求两耦合线圈的端电压41和42。 乎,=L,+Mi2 dt 1 dΨ2, Ψ2=L2i2+Mi1 dt M dt d2=-50sin(10t) dt 2 =M d di2=-150sin(10)
1 2 1 1 1 2 2 2 5 0 s in (1 0 ) 1 5 0 s in (1 0 ) d i d i u L M t d t d t d i d i u M L t d t d t i1 * * L1 L2 + _u1 + _u2 i M 2 图示电路,i1=10A,i2=5cos(10t),L1=2H,L2=3H, M=1H,求两耦合线圈的端电压u1 和u2 。 1 1 1 1 1 2 2 2 2 2 2 1 , , d Ψ u Ψ L i M i d t d Ψ u Ψ L i M i d t 例

4=L, M d12 dt 2=M di, dt 在正弦交流电路中,其相量形式的方程为 U-joLIi+j@MI2 U2 joMI+joL I2 3j@L2 还可以用电流控制电压源 来表示互感电压的作用。 joMI
i1 * * L1 L2 + _u1 + _u2 i M 2 在正弦交流电路中,其相量形式的方程为 1 1 2 1 2 1 2 2 j j j j U L I M I U M I L I j L1 I 1 I 2 j L2 + – –+ jω M I 2 jω M I 1 + – U 2 + – U 1 还可以用电流控制电压源 来表示互感电压的作用。 1 2 1 1 1 2 2 2 di di u L M dt dt di di u M L dt dt

由同名端及、参考方向确定互感线圈的特性方程 有了同名端,以后表示两个线圈相互作用,就不再 考虑实际绕向,而只画出同名端及参考方向即可。 21=M 21- W21 1=-M
由同名端及u、i参考方向确定互感线圈的特性方程 有了同名端,以后表示两个线圈相互作用,就不再 考虑实际绕向,而只画出同名端及参考方向即可。 t i u M d d 1 21 t i u M d d 1 21 i1 * * + – u21 M i1 * * – + u21 M
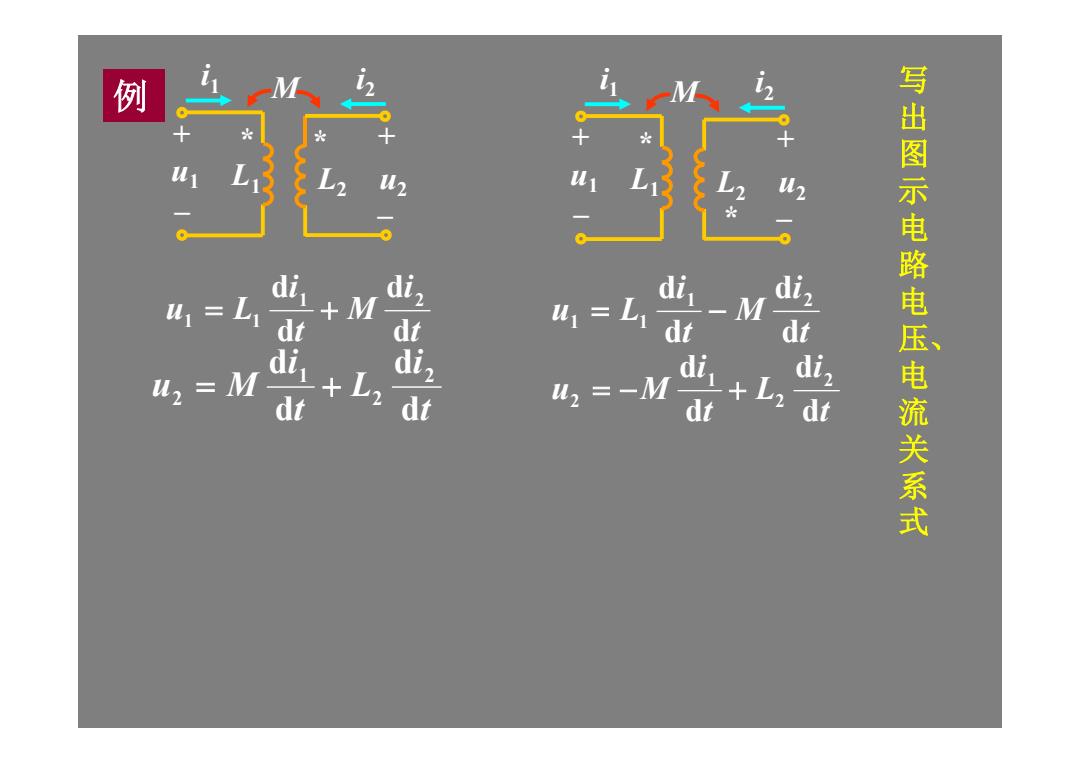
例 M M u, M =-M dt 写出图示电路电压电流关系式
ti M ti u L dd dd 1 2 1 1 ti L ti u M dd dd 2 2 1 2 i1 * * L1 L2 +_u1 +_u2 i M 2 ti M ti u L dd dd 1 2 1 1 ti L ti u M dd dd 2 2 1 2 i1 * * L1 L2 +_u1 +_u2 i 例 M 2 写出图示电路电 压、电流关系式

3.耦合系数(coupling coefficient)k: 工程上为了定量描述两个耦合线圈的耦合程度,把两线 圈的互感磁通链与自感磁通链的比值的几何平均值定义为耦 合因数,用表示。k表示两个线圈磁耦合的紧密程度。 def 12×Ψ21 M n k Ψ11×Ψ22 √L,L2rI(n-r) k≤1。 全耦合:④1①1yD2=①2 L 21 ∴.M2M21=L,L2 M2=LL. .k=1
工程上为了定量描述两个耦合线圈的耦合程度,把两线 圈的互感磁通链与自感磁通链的比值的几何平均值定义为耦 合因数,用k表示。k 表示两个线圈磁耦合的紧密程度。 全耦合: 11= 21,22 =12 d e f 1 2 2 1 1 1 2 2 1 2 ! ! ! M n k L L r n r 1 11 2 22 1 2 1 2 2 21 1 12 12 12 1 2 2 12 21 1 2 1 2 , , , 1 N Φ N Φ L L i i N Φ N Φ M M i i M M L L M L L k k1。 3. 耦合系数 (coupling coefficient) k: