第3次课2学时 教师教案 .3离散时间信号的傅里叶变换和z变换 授课章节 .4离散时间系统 授课方式 ■理论课口讨论课口实验课口习题课 口其他 、熟悉Z变换的意义及与DIFT(离散时间傅里叶变换)的关系: 课堂教学业、 掌握Z正变换和其反变换的计算方法: 目的及要郎、掌握典型序列Z变换的收敛域(双边,因果,左、右序列): 求 4、 熟悉Z变换的主要性质与定理; 5、 掌握离散时间系统线性、时不变性、因果稳定性的判定; 课堂教学 重点:Z正变换和其反变换性质与定理;LSI系统因果稳定性的判定 重点及难 难点:典型序列Z变换的收敛域 点 教学过程 教学方法及 手段 (一)Z变换 举例讲解、 1、序列的傅里叶变换(DTT)的定义 多媒体讲解 xe)=2xmem 2、序列的z变换与Z逆变换 正:X()= 2xm2”, R-<<R 反:x(n)= ()ce(RR C为环形解析域(收敛域)内环绕原点的一条逆时 教学过程 针闭合单围线 3、 Z变换和DT℉T的关系:Z变换是单位圆上的傅里叶变换 Xe以=立xm=Xe) 4、典型序列的收敛域 有限序列全z面,零和无穷要察看: im=] 个jmz] Re[=] Re[=]
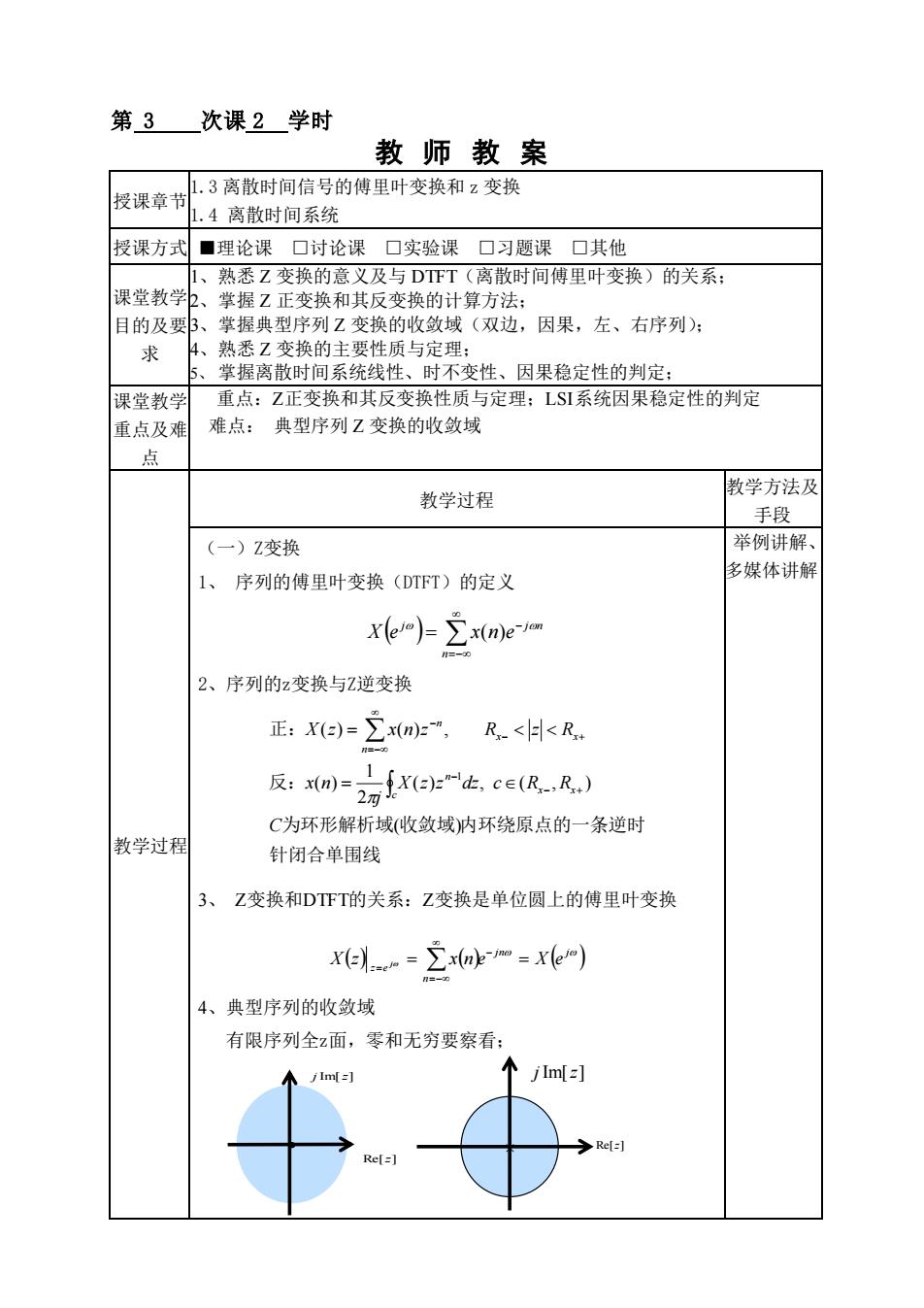
第 3 次课 2 学时 教 师 教 案 授课章节1.3 离散时间信号的傅里叶变换和 z 变换 1.4 离散时间系统 授课方式 ■理论课 □讨论课 □实验课 □习题课 □其他 课堂教学 目的及要 求 1、熟悉 Z 变换的意义及与 DTFT(离散时间傅里叶变换)的关系; 2、掌握 Z 正变换和其反变换的计算方法; 3、掌握典型序列 Z 变换的收敛域(双边,因果,左、右序列); 4、熟悉 Z 变换的主要性质与定理; 5、 掌握离散时间系统线性、时不变性、因果稳定性的判定; 课堂教学 重点及难 点 重点:Z正变换和其反变换性质与定理;LSI系统因果稳定性的判定 难点: 典型序列 Z 变换的收敛域 教学过程 教学过程 教学方法及 手段 (一)Z变换 1、 序列的傅里叶变换(DTFT)的定义 ( ) =− − = n j j n X e x n e ( ) 2、序列的z变换与Z逆变换 针闭合单围线 为环形解析域 收敛域 内环绕原点的一条逆时 反: 正: ( ) ( ) , ( , ) 2 1 ( ) ( ) ( ) , 1 C X z z dz c R R j x n X z x n z R z R x x c n x x n n − + − − + =− − = = 3、 Z变换和DTFT的关系:Z变换是单位圆上的傅里叶变换 ( ) ( ) ( ) jn j n z e X z j = x n e = X e − =− = 4、典型序列的收敛域 有限序列全z面,零和无穷要察看; 举例讲解、 多媒体讲解 Re[z] j Im[z] Re[z] j Im[z]
右边序列圆外面,因果敛至无穷远: iIm[z] 收敛域 左边序列圆里面,逆向因果含零点: 个jm] 个m] R 5=2 =2 双边序列是圆环,边界考虑零极点。 jIm[z] Re[z] 5、Z变换的基本性质和定理 1)线性 2)序列的移位 3)初值定理 4)终值定理 5)序列的卷积和(时域卷积定理) (二)离散时间系统 1、系统模型 x(n) y(n 时域离散系统 TT·1 2、线性:线性系统具有均匀性和迭加性 举例说明
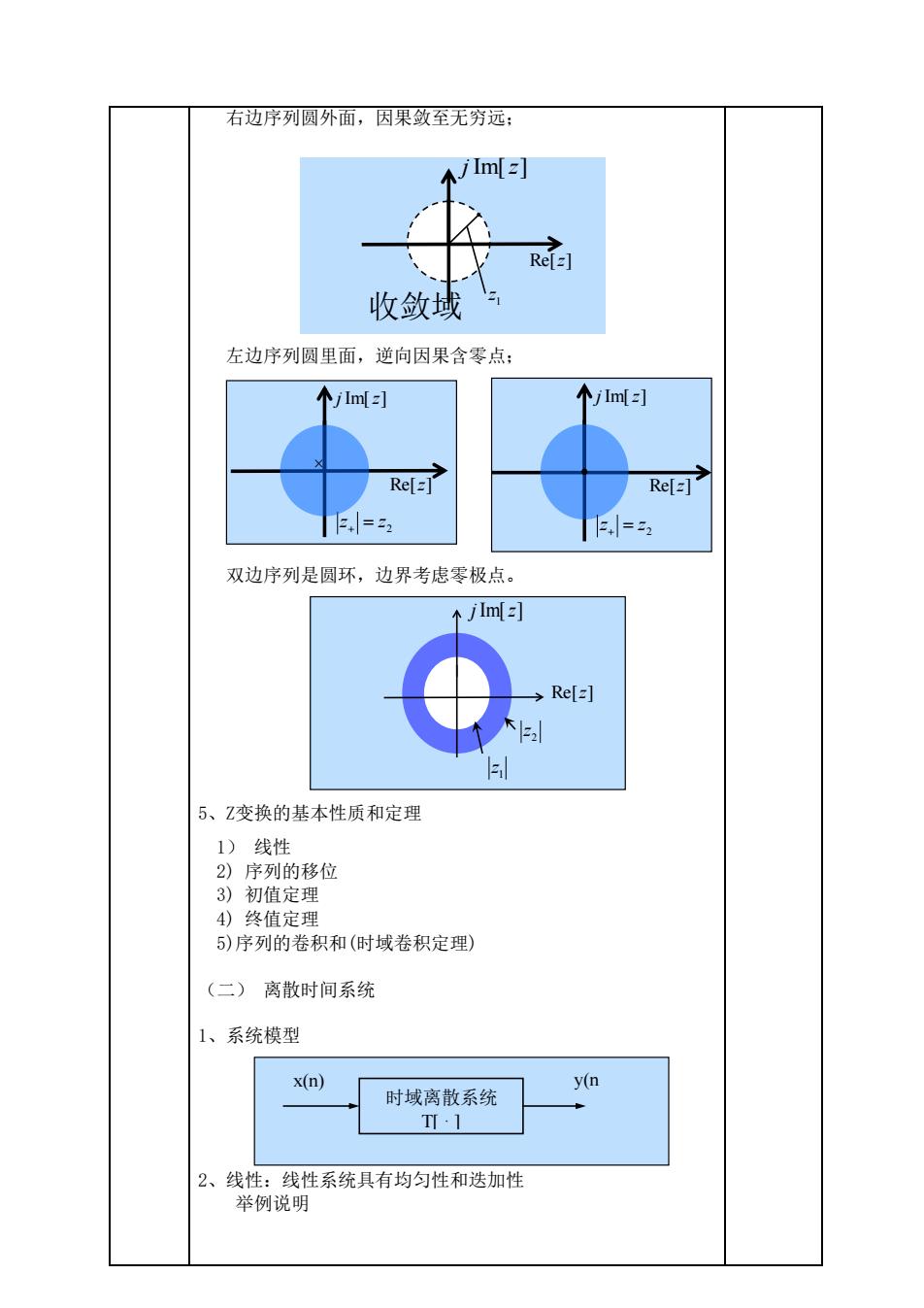
右边序列圆外面,因果敛至无穷远; 左边序列圆里面,逆向因果含零点; 双边序列是圆环,边界考虑零极点。 5、Z变换的基本性质和定理 1) 线性 2) 序列的移位 3) 初值定理 4) 终值定理 5)序列的卷积和(时域卷积定理) (二) 离散时间系统 1、系统模型 2、线性:线性系统具有均匀性和迭加性 举例说明 1 z Re[z] j Im[z] 收敛域 Re[z] j Im[z] 2 z = z + Re[z] j Im[z] 2 z = z + 1 z Re[z] j Im[z] 2 z 时域离散系统 T[ · ] x(n) y(n )

3、时不变性:系统参数不随时间变化的系统,亦即系统对于输 入信号的响应与信号加于系统的时间无关。 举例说明 4、线性时不变系统:一个LSI系统可以用单位脉冲响应h(n)来表 征,任意输入的系统输出等于输入序列和该单位脉冲响应h(n)的 卷积和。 y(n)=x(n)*h(n) 5、因果系统:若系统n时刻的输出,只取决于n时刻以及n时刻 以前的输入序列,而与时刻以后的输入无关,则称该系统为因 果系统。LSI系统是因果系统的充要条件: h(n)=0,n<0 6、稳定系统:输入序列有界,输出必有界的系统。LSI系统是 稳定系统的充要条件: 立hl=M<o 思考题:Z变换存在的条件,Z变换域DTFT的联系 课后作业 与思考题 习题:1.7(4),1.13(3) 本章节的部分内容已在信号与系统中学习过,所以尽管本节的内容比较多,但多数同学能 课后 够很快掌握。 小结 授课教师签名:张培珍 2007年3月13日 注:每项页面大小可根据实际情况自行添减
3、时不变性:系统参数不随时间变化的系统,亦即系统对于输 入信号的响应与信号加于系统的时间无关。 举例说明 4、线性时不变系统:一个LSI系统可以用单位脉冲响应h(n)来表 征,任意输入的系统输出等于输入序列和该单位脉冲响应h(n)的 卷积和。 y(n) = x(n) * h(n) 5、因果系统:若系统 n时刻的输出,只取决于n时刻以及n时刻 以前的输入序列,而与n时刻以后的输入无关,则称该系统为因 果系统。 LSI系统是因果系统的充要条件: h(n) = 0,n 0 6、稳定系统:输入序列有界,输出必有界的系统。 LSI系统是 稳定系统的充要条件: = + =− h n M n ( ) 课后作业 与思考题 思考题:Z 变换存在的条件,Z 变换域 DTFT 的联系 习题:1.7(4),1.13(3) 课后 小结 本章节的部分内容已在信号与系统中学习过,所以尽管本节的内容比较多,但多数同学能 够很快掌握。 授课教师签名:张培珍 2007 年 3 月 13 日 注:每项页面大小可根据实际情况自行添减

第4次课2学时 教师教案 授课章节 .5系统的频率响应与系统函数 授课方式 ■理论课口讨论课 口实验课 口习题课 口其他 课堂教学 掌握系统的频率响应与系统函数 目的及要求 掌握系统函数的零极点特性 课堂教学 重点:什么是频率响应和系统函数 重点及难点 难点:如何利用系统函数的零极点来判断系统的稳定性与因果性 教学过程 教学方法及手 段 1.系统函数:线性时不变系统h()为单位脉冲响应,单位脉 举例讲解、多 冲响应的Z变换称为系统函数。 媒体讲解 Y(=)=X(=).H().H()= Y(=) X(2) 2、频率响应:H(z)称作线性移不变系统的系统函数,而在单 位圆 上的系统函数就是系统的频率响应。即 H(e)hnem t) x(e) 教学过程 3、用系统函数的极点分布分析系统的因果性和稳定性 1)因果:其单位脉冲响应h(n)=0,n<0:那么系统的收敛域 一定包括无穷点,收敛域在某一圆外 R-<☑<o 2)稳定:h(n)的z变换的收敛域: hm 说明:稳定系统的系统函数(z)的收敛域须包含单位圆 3)因果稳定:H(z)须从单位圆到c的整个z域内收敛即系 统函数H(2)的全部极点必须在单位圆内 r<≤o,0<r<1 4、利用系统函数的零极点分布分析系统的频率特性
第 4 次课 2 学时 教 师 教 案 授课章节 1.5 系统的频率响应与系统函数 授课方式 ■理论课 □讨论课 □实验课 □习题课 □其他 课堂教学 目的及要求 掌握系统的频率响应与系统函数 掌握系统函数的零极点特性 课堂教学 重点及难点 重点:什么是频率响应和系统函数 难点:如何利用系统函数的零极点来判断系统的稳定性与因果性 教学过程 教学过程 教学方法及手 段 1.系统函数:线性时不变系统h(n)为单位脉冲响应,单位脉 冲响应的Z变换称为系统函数。 ( ) ( ) ( ) ( ) ( ), ( ) X z Y z Y z = X z • H z H z = 2、频率响应:H(z)称作线性移不变系统的系统函数,而在单 位圆 上的系统函数就是系统的频率响应。即 j n n j H e h n e − =− ( ) = ( ) ( ) ( ) ( ) j j j X e Y e H e = 3、用系统函数的极点分布分析系统的因果性和稳定性 1)因果:其单位脉冲响应h(n)=0,n<0;那么系统的收敛域 一定包括无穷点,收敛域在某一圆外 R − Z X 2)稳定:h(n)的z变换的收敛域: =− − n n h(n)z 说明:稳定系统的系统函数H(z)的收敛域须包含单位圆 3)因果稳定:H(z)须从单位圆到 的整个z域内收敛即系 统函数H(z)的全部极点必须在单位圆内 r z ,0 r 1 4、利用系统函数的零极点分布分析系统的频率特性 举例讲解、多 媒体讲解
Y() - H(z)= m=0 X() 对上式进行因式分解: M Y(=K -ce) H(z)= X() Π1-d,) 式中c,是H(亿)在Z平面的零点,d,是H(亿)在Z平面的极点, 除了K以外,整个系统函数可以用它的全部零、极点来 唯一确定。 频率响应的几何确定 即用极点和零点来表示系统函数: M M 1-cz) (e-c) H()=K Π-d,-) Πe-d) 系统的频率响应为: e"-e) H(ejo)=Kei(N-M)o H(e) Π(e-d) 个jIm[z] Φk Tk Relz] Cm om Cm 思考题: LSI系统的Z域描述 系统函数H)=只与系统频响 课后作业 Y(e) X(E) H(e")= 的物理意义: 与思考题 X(em) 习题:1.22 本章己经结束,可以看出本课程逻辑性很强,先难后易,前三章有一定的难度,鉴于此,建 课后 议的学习方法是:预习,课堂上认真听讲,必须记笔记,但要注意以听为主。 小结 授课教师签名:张培珍 2007年3月15日 注:每项页面大小可根据实际情况自行添减
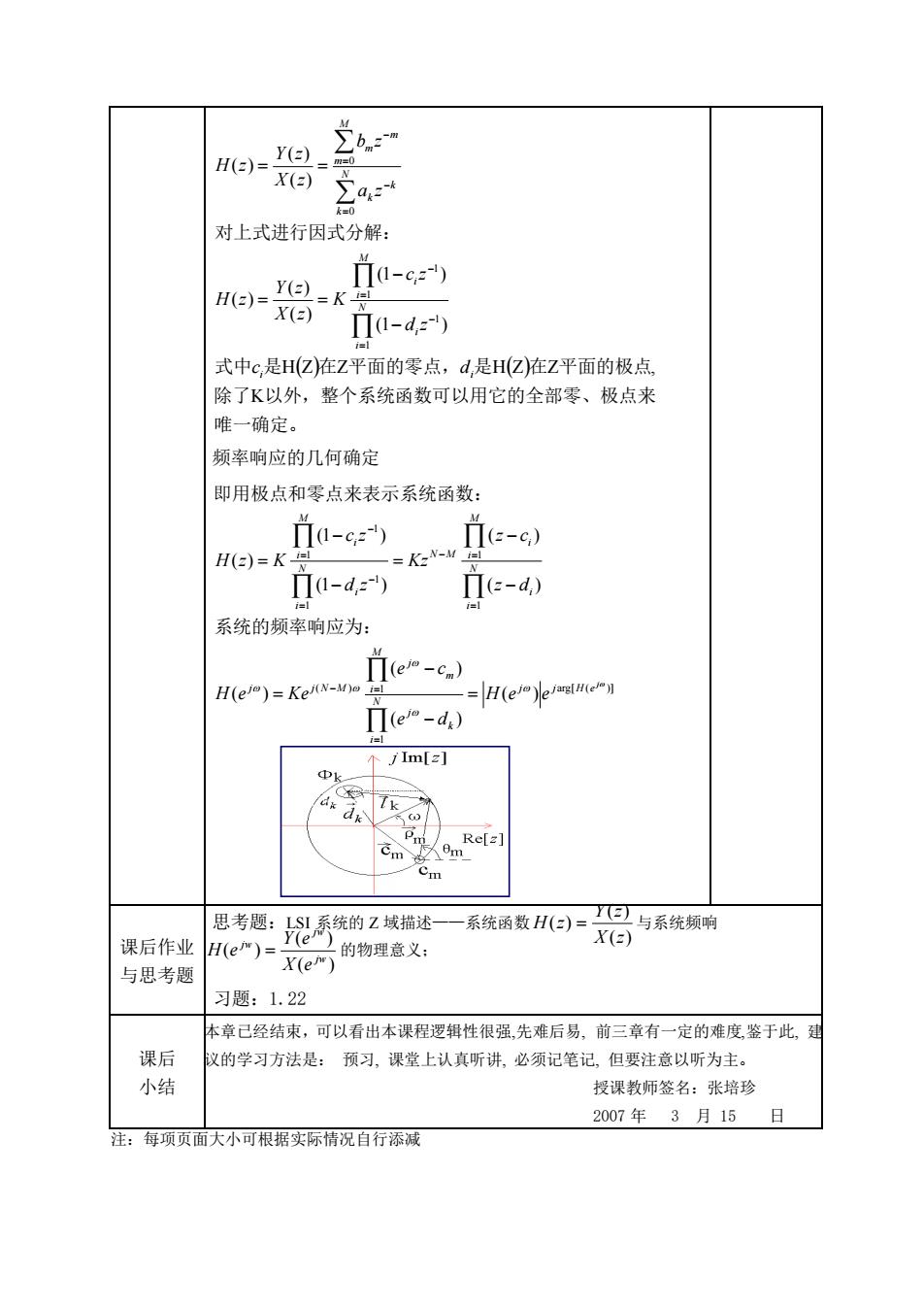
( ) ( ) 唯一确定。 除了 以外,整个系统函数可以用它的全部零、极点来 式中 是 在 平面的零点, 是 在 平面的极点 对上式进行因式分解: K H Z Z H Z Z , (1 ) (1 ) ( ) ( ) ( ) ( ) ( ) ( ) 1 1 1 1 0 0 i i N i i M i i N k k k M m m m c d d z c z K X z Y z H z a z b z X z Y z H z = − = − = − = − − − = = = = 频率响应的几何确定 arg[ ( )] 1 ( ) 1 1 1 1 1 1 1 ( ) ( ) ( ) ( ) ( ) ( ) (1 ) (1 ) ( ) j j j H e N i k j M i m j j j N M N i i M i i N M N i i M i i H e e e d e c H e Ke z d z c Kz d z c z H z K = − − = − − = − − = = − = = − = = − = − 系统的频率响应为: 即用极点和零点来表示系统函数: 课后作业 与思考题 思考题:LSI 系统的 Z 域描述——系统函数 ( ) ( ) ( ) X z Y z H z = 与系统频响 ( ) ( ) ( ) jw jw jw X e Y e H e = 的物理意义; 习题:1.22 课后 小结 本章已经结束,可以看出本课程逻辑性很强,先难后易, 前三章有一定的难度,鉴于此, 建 议的学习方法是: 预习, 课堂上认真听讲, 必须记笔记, 但要注意以听为主。 授课教师签名:张培珍 2007 年 3 月 15 日 注:每项页面大小可根据实际情况自行添减