also an important tool of automaticcon,management scn,and soon The purpose of teaching is to improve the students'ability of abstract thinking and logical reasoning and learn the description tools and necessary theoretical basis for the application in computer,and follow-up courses to lay a good foundation (二)课程目标 课程目标1:理解离散数学中命题逻辑、谓词逻辑、二元关系、集合论、图论等知识的 基本概念、理论和知识,初步掌握计算机复杂工程问题中离散结构的描述、提炼和表达方法 能力,提升严谨镇密的数学思维。 课程目标2:运用现代数学的观点和方法,理解并掌握处理离散结构的实用模型与算法 初步具备对计算机工程问题的建模、分析和优化能力,培养离散数学在实际工程问题中的应 用能力。 课程目标3:通过最短路径、者色问题、哈夫曼算法等内容的学习,注重离散化的数学 素养培养和思维方式锻炼,进一步应用在解决计算机复杂工程问题中,提高面向计算机复杂 工程问题中的抽象思维、概括分析、逻辑推理的能力。 课程目标4(思政目标):了解数理逻辑的发展历史、集合论中经典的“理发师”悖论、 图论对计算机各个方向的科学意义等内容,能演绎数学曲折上升的发展历程,树立坚定的科 学信念,形成科学的世界观、人生观和价值观,并不断地提高自身的科学素养。 (三)课程目标和毕业婴求的对应关系 课程日标 毕业要求指标点 毕业要求 .工程知识 2-2 2.问题分析 41 4.研究 12-1 12.终身学习 三、教学内容、要求与学时分配 教学内容 重点、难点 学散学方式( 支撑词 预期学习成果 授、实验、上 时 程目标 机、讨论) 第一章命题逻辑 能够区分不同链结词重点:联结词在自然语 (1)命题及命题联结词,命题公式及类型的食义,能姚对命腰言中的含义,命假符号 (2)等值演算,联结词全功修集:荒式, 符号化。能够证明一化:范式的写法及应 3 (3)推理理论 个公式是永真式 ”用 思政融入点:通过数理逻辑的发展历史 够格命题公式转化为难点:永真式、永真道 展示数学曲折上升的发展历程,正确认识范式 含式,等价公式的证明 自主及终身学习的必要性 方法
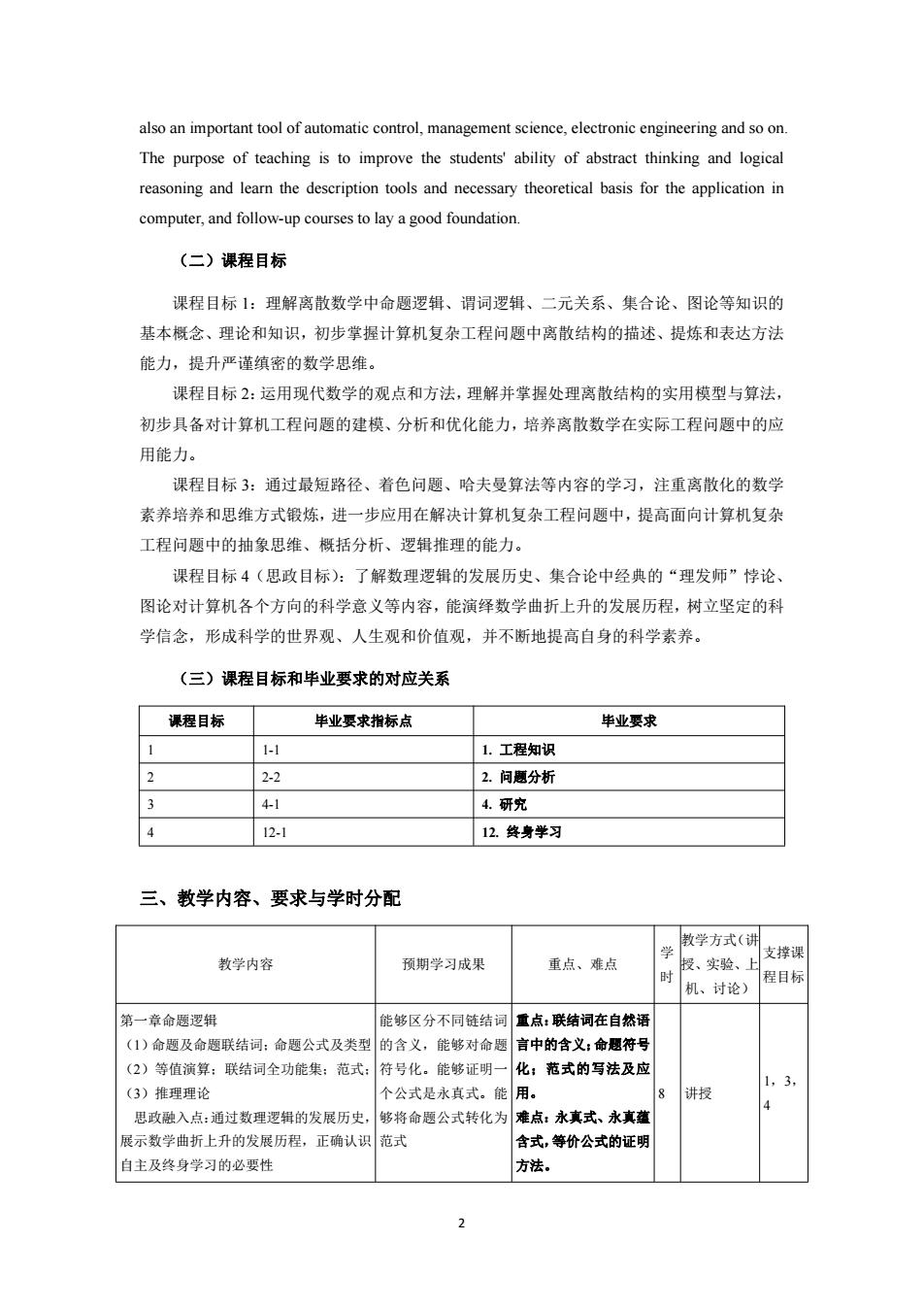
2 also an important tool of automatic control, management science, electronic engineering and so on. The purpose of teaching is to improve the students' ability of abstract thinking and logical reasoning and learn the description tools and necessary theoretical basis for the application in computer, and follow-up courses to lay a good foundation. (二)课程目标 课程目标 1:理解离散数学中命题逻辑、谓词逻辑、二元关系、集合论、图论等知识的 基本概念、理论和知识,初步掌握计算机复杂工程问题中离散结构的描述、提炼和表达方法 能力,提升严谨缜密的数学思维。 课程目标 2:运用现代数学的观点和方法,理解并掌握处理离散结构的实用模型与算法, 初步具备对计算机工程问题的建模、分析和优化能力,培养离散数学在实际工程问题中的应 用能力。 课程目标 3:通过最短路径、着色问题、哈夫曼算法等内容的学习,注重离散化的数学 素养培养和思维方式锻炼,进一步应用在解决计算机复杂工程问题中,提高面向计算机复杂 工程问题中的抽象思维、概括分析、逻辑推理的能力。 课程目标 4(思政目标):了解数理逻辑的发展历史、集合论中经典的“理发师”悖论、 图论对计算机各个方向的科学意义等内容,能演绎数学曲折上升的发展历程,树立坚定的科 学信念,形成科学的世界观、人生观和价值观,并不断地提高自身的科学素养。 (三)课程目标和毕业要求的对应关系 课程目标 毕业要求指标点 毕业要求 1 1-1 1. 工程知识 2 2-2 2. 问题分析 3 4-1 4. 研究 4 12-1 12. 终身学习 三、教学内容、要求与学时分配 教学内容 预期学习成果 重点、难点 学 时 教学方式(讲 授、实验、上 机、讨论) 支撑课 程目标 第一章命题逻辑 (1)命题及命题联结词;命题公式及类型 (2)等值演算;联结词全功能集;范式; (3)推理理论 思政融入点:通过数理逻辑的发展历史, 展示数学曲折上升的发展历程,正确认识 自主及终身学习的必要性 能够区分不同链结词 的含义,能够对命题 符号化。能够证明一 个公式是永真式。能 够将命题公式转化为 范式 重点:联结词在自然语 言中的含义;命题符号 化;范式的写法及应 用。 难点:永真式、永真蕴 含式,等价公式的证明 方法。 8 讲授 1,3, 4
教学方式(用 教学内容 预期学习成果 重点、难点 机、讨论 能够对合题符号化,重点:调词公式及命题 第二音一阶罗组 会用等价公式求谓词符号化 (1)一阶罗组概今 (2)一阶逻细合式公式及解 公式的真值。能够将 难点,词算的价 3 (3)等值式,前范式 胃词公式写为前束花 公 试和 真蕴含式的 证明方法 第三章集合的基本概念和运算 (1)生合据今 能够解释集合的三种重点:集合的定义和基 (2)集合基本运算公式 定义方式,会求集合 本运算。 (3)集合中元素计数(包含排斥原理 的基本运算以及系 讲授 1,2 思政融入点:通过集合论中经典的 理》 集。会用排斥原理解难点:集合的幂集,排 师”悖论,展示数学曲折上升的发展历程 决集合的计数问题。 斥原理。 正确认识自主及终身学习的必要性 第四章二元关系和函数 重点:关系的性质,关 (1)笛卡尔积: 二元关系概念和性质 系的复合,求逆,等价 (2)二元关系运算:关系闭包:等价关系 关系,函数的定义 偏序关系: 14讲投 1,3 (3)函数定义和性质:复合函数和反函数 难点:关系的闭包,等 第五章图的基木概念 能够概述图的基本概 (1)无向图:有向图:握手定理: ,判定无向图的连 计算连通分 重点:有向图和无向 (2)通路、回路、图的连通:图的矩阵表 通性。 的概念,图的连通性 判定有向图的可 可达性,图的矩阵表示 3)最短路径和关键路径 讲授 1,2 性,判定强连通和露 思政融入点:通过图论对计算机科学的意 联通,能够给出图的 义,展示数学曲折上升的发展历程,正确矩阵表示, 概述最 难点:图的最短路径 认识自主及终身学习的必要性 路径的计算方法。 第六章特殊的图 重点:二部图、欧拉图 1)一部图 能够概述二部图、欧哈密图的定义 (2)欧拉图 粒图、哈密顿图的 讲按 ,2 (3)哈密倾图 难点:二部图、欧拉图 哈密顿图的判定 第上音射 重点:树的定义,生成 (1)树的念:树的等价定理 树的摄念 (2)无向树的 (3)根树及其应用。 难点:最小生成树的求 法,根树的定义及应用
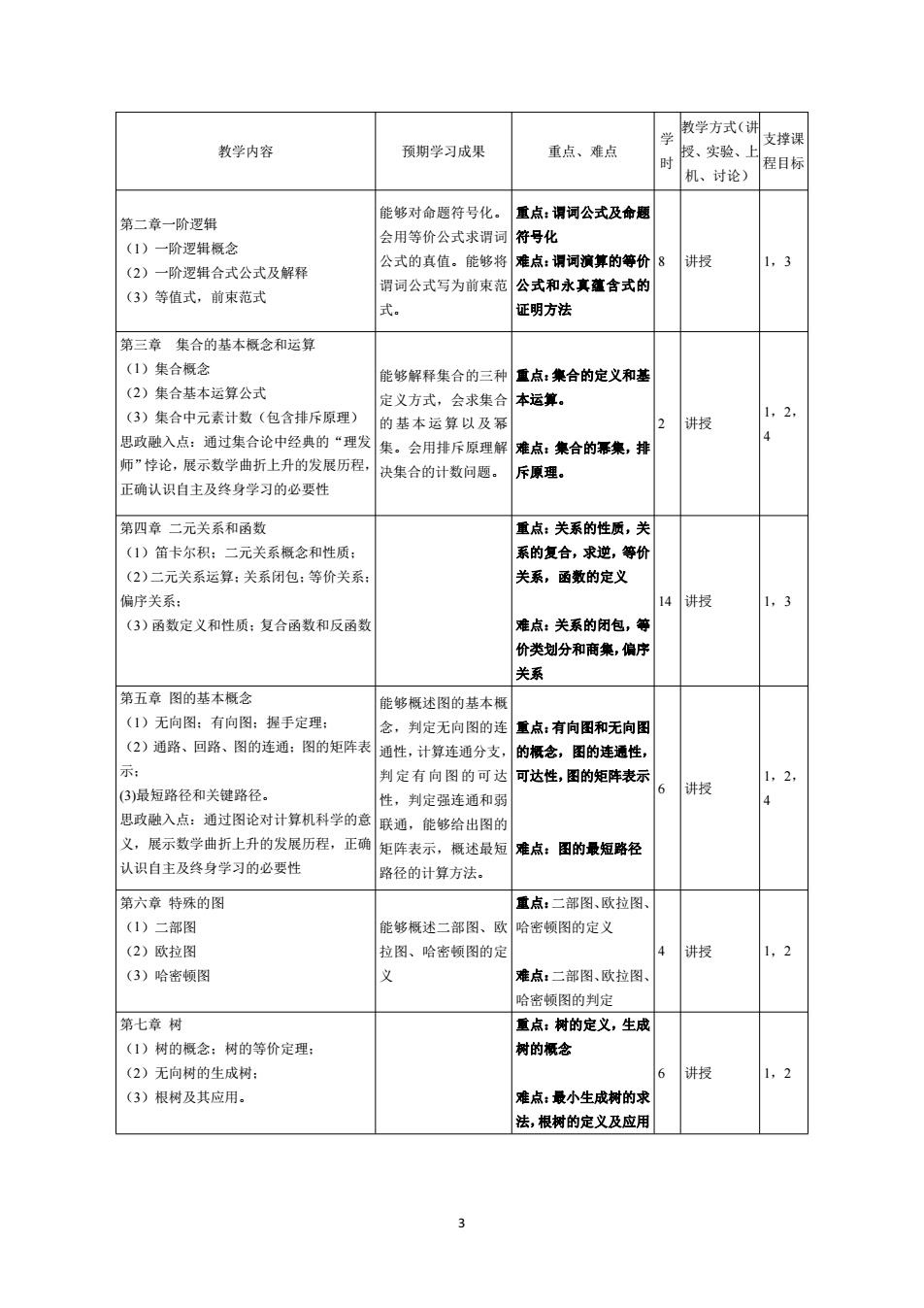
3 教学内容 预期学习成果 重点、难点 学 时 教学方式(讲 授、实验、上 机、讨论) 支撑课 程目标 第二章一阶逻辑 (1)一阶逻辑概念 (2)一阶逻辑合式公式及解释 (3)等值式,前束范式 能够对命题符号化。 会用等价公式求谓词 公式的真值。能够将 谓词公式写为前束范 式。 重点:谓词公式及命题 符号化 难点:谓词演算的等价 公式和永真蕴含式的 证明方法 8 讲授 1,3 第三章 集合的基本概念和运算 (1)集合概念 (2)集合基本运算公式 (3)集合中元素计数(包含排斥原理) 思政融入点:通过集合论中经典的“理发 师”悖论,展示数学曲折上升的发展历程, 正确认识自主及终身学习的必要性 能够解释集合的三种 定义方式,会求集合 的 基本 运 算 以及 幂 集。会用排斥原理解 决集合的计数问题。 重点:集合的定义和基 本运算。 难点:集合的幂集,排 斥原理。 2 讲授 1,2, 4 第四章 二元关系和函数 (1)笛卡尔积;二元关系概念和性质; (2)二元关系运算;关系闭包;等价关系; 偏序关系; (3)函数定义和性质;复合函数和反函数 重点:关系的性质,关 系的复合,求逆,等价 关系,函数的定义 难点:关系的闭包,等 价类划分和商集,偏序 关系 14 讲授 1,3 第五章 图的基本概念 (1)无向图;有向图;握手定理; (2)通路、回路、图的连通;图的矩阵表 示; (3)最短路径和关键路径。 思政融入点:通过图论对计算机科学的意 义,展示数学曲折上升的发展历程,正确 认识自主及终身学习的必要性 能够概述图的基本概 念,判定无向图的连 通性,计算连通分支, 判 定有 向 图 的可 达 性,判定强连通和弱 联通,能够给出图的 矩阵表示,概述最短 路径的计算方法。 重点:有向图和无向图 的概念,图的连通性, 可达性,图的矩阵表示 难点:图的最短路径 6 讲授 1,2, 4 第六章 特殊的图 (1)二部图 (2)欧拉图 (3)哈密顿图 能够概述二部图、欧 拉图、哈密顿图的定 义 重点:二部图、欧拉图、 哈密顿图的定义 难点:二部图、欧拉图、 哈密顿图的判定 4 讲授 1,2 第七章 树 (1)树的概念;树的等价定理; (2)无向树的生成树; (3)根树及其应用。 重点:树的定义,生成 树的概念 难点:最小生成树的求 法,根树的定义及应用 6 讲授 1,2
四、课程考核评价方式 考核以课程目标的达成度为主要目的,以检查学生对各知识点的掌握程度和应用能力为 重要内容。 (一)考核方式 考核方式为闭卷笔试。考试课程成绩由期末成绩(70%)、阶段练习(20%)、作业(10%) 构成。 (二)课程成绩 (1)期末考试:采用闭卷笔试形式。考试范围几乎通盖所有讲授的内容,考试内容应 能客观反映出学生对本门课程主要内容的理解、掌握程度及综合运用能力。 (2)阶段练习:设置3次及以上的阶段练习(数理逻辑、二元关系、图论),阶段练习 用以巩固知识或拓展总结,对于作业中的共性问愿,教师须在课堂讲解,以帮助学生提供和 进步。任一次阶段考不通过不可进入下一个环节的考核。 (3)作业:平时作业量应不少于24学时,在每个小节讲授完之后,要布置一定量的作 业,旨在加深学生对所学知识的理解、运用。作业批改以抽查的方式,通过批改了解学生对 本小节内容的掌握情况,及时解决在作业中集中存在的问题,加深学生对知识的理解。 1,考核环节及说明 成绩构成考核说明 (1)平时成绩满分为100分,占总成绩的30% 平时成绩 (2)针对平时成绩对应的课程目标,由作业、测验、实验、课堂表现等部分构成,各部分 占比及评分标准由教师根据实际情况决定。 (1)考试方式及占比:采用闭卷笔试,考试成绩100分,占课程考核成绩的70%. (2)评宁依据,老试成的评宁相据试卷酸老答室和评分标准讲行。 末考试 (3)考试题型:选择题、填空 、计算题和证明 (4)考试内容:涵盖所有讲授的内容. 2.考核与评价方式 成绩比例(平时成绩309%+期末成70%) 课程目标 平时成绩(30%) 合计 作业(10% 期末成绩(70%) 测验(20% 4 22 28 2 4 10 23 37 3 4 2 21 4 合计成绩构成) 10 20 70 100%
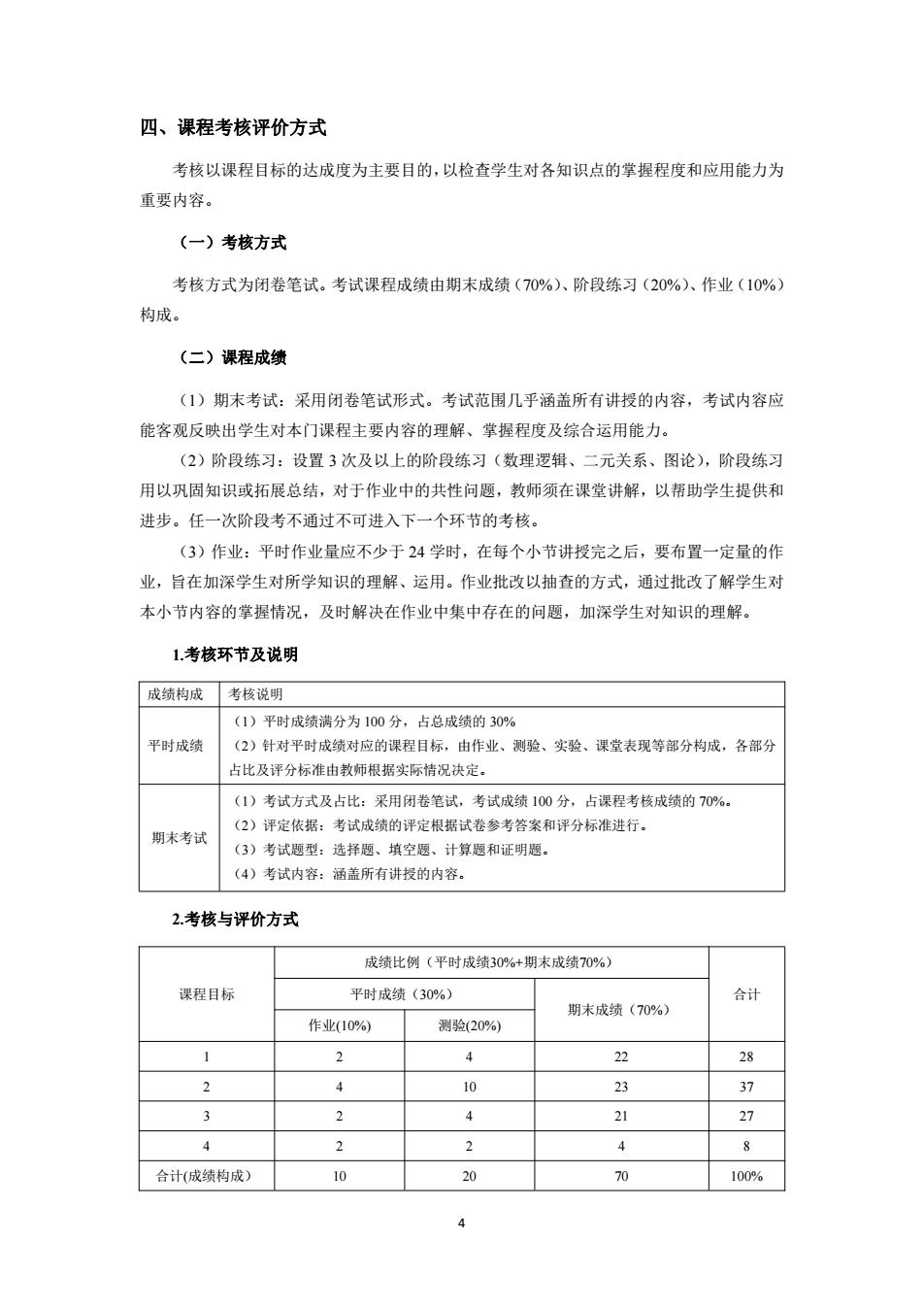
4 四、课程考核评价方式 考核以课程目标的达成度为主要目的,以检查学生对各知识点的掌握程度和应用能力为 重要内容。 (一)考核方式 考核方式为闭卷笔试。考试课程成绩由期末成绩(70%)、阶段练习(20%)、作业(10%) 构成。 (二)课程成绩 (1)期末考试:采用闭卷笔试形式。考试范围几乎涵盖所有讲授的内容,考试内容应 能客观反映出学生对本门课程主要内容的理解、掌握程度及综合运用能力。 (2)阶段练习:设置 3 次及以上的阶段练习(数理逻辑、二元关系、图论),阶段练习 用以巩固知识或拓展总结,对于作业中的共性问题,教师须在课堂讲解,以帮助学生提供和 进步。任一次阶段考不通过不可进入下一个环节的考核。 (3)作业:平时作业量应不少于 24 学时,在每个小节讲授完之后,要布置一定量的作 业,旨在加深学生对所学知识的理解、运用。作业批改以抽查的方式,通过批改了解学生对 本小节内容的掌握情况,及时解决在作业中集中存在的问题,加深学生对知识的理解。 1.考核环节及说明 成绩构成 考核说明 平时成绩 (1)平时成绩满分为 100 分,占总成绩的 30% (2)针对平时成绩对应的课程目标,由作业、测验、实验、课堂表现等部分构成,各部分 占比及评分标准由教师根据实际情况决定。 期末考试 (1)考试方式及占比:采用闭卷笔试,考试成绩 100 分,占课程考核成绩的 70%。 (2)评定依据:考试成绩的评定根据试卷参考答案和评分标准进行。 (3)考试题型:选择题、填空题、计算题和证明题。 (4)考试内容:涵盖所有讲授的内容。 2.考核与评价方式 课程目标 成绩比例(平时成绩30%+期末成绩70%) 平时成绩(30%) 合计 期末成绩(70%) 作业(10%) 测验(20%) 1 2 4 22 28 2 4 10 23 37 3 2 4 21 27 4 2 2 4 8 合计(成绩构成) 10 20 70 100%

五、教学方法 在课堂上应详细讲授每章的重点、难点内容:讲授中应注重通过必要的案例演示,启发、 调动学生的思维,加深学生对有关概念、理论等内容的理解,并应采用多媒体辅助教学,加 大课堂授课的知识含量。教师应及时了解学生学习过程中遇到的问题,给予及时的指导,对 共性问题,在课堂上予以讲解和演示。要注意培养学生的自学能力,在教学中注意引导学生 自己提出问题,分析问题,培养他们独立解决问题的能力。 使用多媒体教学,以PPT显示教学提纲,本课程采用的教学媒体主要有:文字教材、 课件。课件课后提供给学生。对学生的辅导,主要采用当面答疑、集体辅导、E.ML、QQ 微信等形式)。 六、参考材料 教材: 1.耿素云,屈婉玲,张立品.《离散数学》,清华大学出版社,2021年11月,第六版。 参考书目: 1.歌素云,屈婉玲,张立昂.《离散数学题解》,清华大学出版社,2021年12月,第六版 2.傅彦,顾小丰,王庆先,刘启和.《离散数学及共应用》,高等教有出版社,2020年7月, 第三版 3.Kenneth Rosen著.徐六通,杨娟,吴斌译.《离散数学及其应用》.机械工业出版社 2020年1月,本科教学版. 4.董晓蕾,曹珍富.《离散数学》.机械工业出版社,2009年1月,第一版, 主撰人:张文博 审核人:卢鹏、王文娟 英文校对:王文娟 教学副院长:袁红春 日期:2022年9月5日 5
5 五、教学方法 在课堂上应详细讲授每章的重点、难点内容;讲授中应注重通过必要的案例演示,启发、 调动学生的思维,加深学生对有关概念、理论等内容的理解,并应采用多媒体辅助教学,加 大课堂授课的知识含量。教师应及时了解学生学习过程中遇到的问题,给予及时的指导,对 共性问题,在课堂上予以讲解和演示。要注意培养学生的自学能力,在教学中注意引导学生 自己提出问题,分析问题,培养他们独立解决问题的能力。 使用多媒体教学,以 PPT 显示教学提纲,本课程采用的教学媒体主要有:文字教材、 课件。课件课后提供给学生。对学生的辅导,主要采用当面答疑、集体辅导、E-MAIL、QQ、 微信等形式)。 六、参考材料 教材: 1. 耿素云, 屈婉玲, 张立昂. 《离散数学》,清华大学出版社, 2021 年 11 月,第六版。 参考书目: 1. 耿素云, 屈婉玲, 张立昂. 《离散数学题解》. 清华大学出版社, 2021 年 12 月,第六版 2. 傅彦, 顾小丰, 王庆先, 刘启和.《离散数学及其应用》,高等教育出版社, 2020 年 7 月, 第三版 3. Kenneth Rosen 著. 徐六通, 杨娟, 吴斌 译. 《离散数学及其应用》. 机械工业出版社, 2020 年 1 月,本科教学版. 4. 董晓蕾, 曹珍富. 《离散数学》. 机械工业出版社, 2009 年 1 月,第一版. 主撰人:张文博 审核人:卢鹏、王文娟 英文校对:王文娟 教学副院长:袁红春 日 期:2022 年 9 月 5 日

附件:各类考核与评价标准表 考核方式里有几种类型,就写几种评分标准,参考如下: 1.作业评分标准 、成绩 良好 中等 及格 优秀 不及格 (78≤分数 (68≤分数<(60≤分数< 课程目标 (分数290分) 90) (分数<60分) 78) 68) 按时交作业 按时交作业,基基本按时交作基本按时交作 有多次缺勤,不能 本概念表 本概念表述正 业,基本概念 业,基本度 按时交作业 有 深程目标1 正确,论述划 确,论述泛辑而 述正确,论述逐 述基本正确、论 袭现象,或者基本 粗清楚,尽次 楚,层次分明 辑较错楚,语言述基本清楚,语 概念不清楚、论述 分明,语言规 语言规范 较规范 言较规范 不清楚 按时交作业 按时交作业,登太接时交作某太按时交作右多次缺勒。不能 学程离散结 握离散结构的 按时交作业,有 模型 模型与算法, 袭现象,不能掌拉 课程目标2 法,对课程沟 误程涉及的 与算法,对课形 与媒法,对保性 离散结构的模雪 及的工程问题 程问题进行正 洗及的工程问 涉及的工程问 与算法,对课程洗 进行正确表 确表达、分析和 趣进行较好的 趣进行基本的 及的工程间题不 达、分析和建 表达、分析和建表达、分析和建 能进行正确表达 模 分析和建模 按时交作业, 按时交作业,理 基本按时交作 基本按时交作 有多次缺勤,不能 理解离散化的 解离收化的数 北,较好地理射 化,基本理解离 按时交作业,有抄 数学素养和用 学素养和用组 离散化的数学 散化的学素 芳现象,不能理解 课程目标3 维方式,能能 方式,能够调而 素养和思维方 养和思方式 离散化的数学 调研和分析 和分析计算机 式,较好地调研 基本能够调研 养和思维方式, 算机复杂工程 复杂工程问题 和分析计算制 和分析计算 能调研和分析 问翅, 复杂工程问题 复杂工程题 算机复杂工程同 按时交作业 按时交作业,树基本按时交作 基本按时交作 有多次缺勤,不能 树立正确的数 立正确的学 业,较好树立 业,基本树立正 按时交作业,有抄 学学习观和利 学习观和科号 正确的数学学 确的数学学 现象, 不能树 学的世界观 的世养观、入生 习观和科学的 观和科学的世 正确的数学学 程目标4 人生观和价值 观和价值观, 世界观、人生观 界观、人生观和 观和科学的世界 观。正确认知确认即到白 和价估理,正确价伯型.某杰认 型、人生观和价值 到自主及终身 及终身学习的 认识到自主及 识到自主及终 观。不能正确认识 学习的必要 必要性 终身学习的 身学习的必要 到自主及终身等 要性 习的必要性
6 附件:各类考核与评价标准表 考核方式里有几种类型,就写几种评分标准,参考如下: 1.作业评分标准 成绩 课程目标 优秀 (分数≥90 分) 良好 (78≤分数< 90) 中等 (68≤分数< 78) 及格 (60≤分数< 68) 不及格 (分数<60 分) 课程目标 1 按时交作业, 基本概念表述 正确,论述逻 辑清楚,层次 分明,语言规 范。 按时交作业,基 本概念表述正 确,论述逻辑清 楚,层次分明, 语言规范。 基本按时交作 业,基本概念表 述正确,论述逻 辑较清楚,语言 较规范。 基本按时交作 业,基本概念表 述基本正确、论 述基本清楚,语 言较规范 有多次缺勤,不能 按时交作业,有抄 袭现象,或者基本 概念不清楚、论述 不清楚 课程目标 2 按时交作业, 掌握离散结构 的 模 型 与 算 法,对课程涉 及的工程问题 进 行 正 确 表 达、分析和建 模。 按时交作业,掌 握离散结构的 模型与算法,对 课程涉及的工 程问题进行正 确表达、分析和 建模。 基本按时交作 业,较好掌握离 散结构的模型 与算法,对课程 涉及的工程问 题进行较好的 表达、分析和建 模。 基本按时交作 业,基本掌握离 散结构的模型 与算法,对课程 涉及的工程问 题进行基本的 表达、分析和建 模 有多次缺勤,不能 按时交作业,有抄 袭现象,不能掌握 离散结构的模型 与算法,对课程涉 及的工程问题不 能进行正确表达、 分析和建模 课程目标 3 按时交作业, 理解离散化的 数学素养和思 维方式,能够 调研和分析计 算机复杂工程 问题。 按时交作业,理 解离散化的数 学素养和思维 方式,能够调研 和分析计算机 复杂工程问题。 基本按时交作 业,较好地理解 离散化的数学 素养和思维方 式,较好地调研 和分析计算机 复杂工程问题。 基本按时交作 业,基本理解离 散化的数学素 养和思维方式, 基本能够调研 和分析计算机 复杂工程问题 有多次缺勤,不能 按时交作业,有抄 袭现象,不能理解 离散化的数学素 养和思维方式,不 能调研和分析计 算机复杂工程问 题 课程目标 4 按时交作业, 树立正确的数 学学习观和科 学的世界观、 人生观和价值 观,正确认识 到自主及终身 学 习 的 必 要 性。 按时交作业,树 立正确的数学 学习观和科学 的世界观、人生 观和价值观,正 确认识到自主 及终身学习的 必要性。 基本按时交作 业,较好地树立 正确的数学学 习观和科学的 世界观、人生观 和价值观,正确 认识到自主及 终身学习的必 要性。 基本按时交作 业,基本树立正 确的数学学习 观和科学的世 界观、人生观和 价值观,基本认 识到自主及终 身学习的必要 性 有多次缺勤,不能 按时交作业,有抄 袭现象,不能树立 正确的数学学习 观和科学的世界 观、人生观和价值 观,不能正确认识 到自主及终身学 习的必要性