
齐次微分方程的解答具有下面的形式 uc(t)=e-a[K cos(@t)+K,sin(@at)] Ke cos(@t+P) (9-11) 式中 K=K+K2 =-arctan K2 K 由初始条件,(0)和4c(O)确定常数K1,K,后,得到电容 电压的零输入响应,再利用KCL和VCR方程得到电感电流 的零输入响应
齐次微分方程的解答具有下面的形式 e cos( ) (9 11) ( ) e [ cos( ) sin( )] C 1 2 = + − = + − − K t u t K t K t t t d d d 式中 1 2 2 2 2 1 arctan K K K = K + K = − 由初始条件iL (0)和uC (0)确定常数K1,K2后,得到电容 电压的零输入响应,再利用KCL和VCR方程得到电感电流 的零输入响应
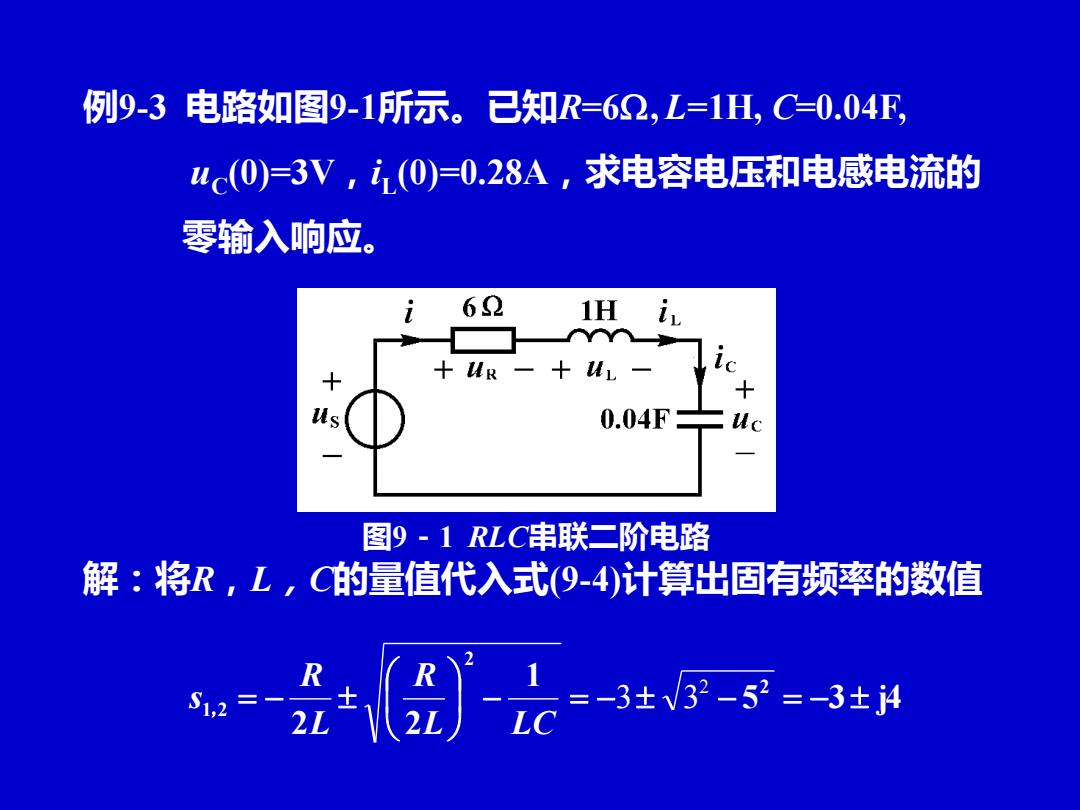
例9-3电路如图9-1所示。己知R=62,L=1H,C-0.04F, 4c(0)=3V,1(0)=0.28A,求电容电压和电感电流的 零输入响应。 62 1H i ic 十 0.04F 图9-1RLC串联二阶电路 解:将R,L,C的量值代入式(9-4)计算出固有频率的数值 S2=- 2
例9-3 电路如图9-1所示。已知R=6, L=1H, C=0.04F, uC (0)=3V,iL (0)=0.28A,求电容电压和电感电流的 零输入响应。 5 3 j4 1 2 2 2 2 1 2 − = − − = − = − 2 3 3 L LC R L R s , 解:将R,L,C的量值代入式(9-4)计算出固有频率的数值 图9-1 RLC串联二阶电路

将两个不相等的固有频率s=-3+j4和S2=-3-j4代入式 (9-11)得到 uc(t)=e[K cos4t+K,sin(4t)] (t≥0) 利用电容电压的初始值4(0)=3V和电感电流的初始值 i(0)=0.28A得到以下两个方程 uc(0)Ki duc(t) dt m=-3K,+4K=0=7 C 求解以上两个方程得到常数K,=3和K,=4,得到电容电 压和电感电流的零输入响应: u (t)=e-[3 cos4t+4sin(4t)]=5e-3/cos(4t-53.1)V (t≥0) =C=0.04eT7cos(4)-24sin(4=e-”cos41+73.74)A
利用电容电压的初始值uC (0)=3V和电感电流的初始值 iL (0)=0.28A得到以下两个方程 7 (0) 3 4 d d ( ) (0) L 0 1 2 C C 1 = − + = = = = C i K K t u t u K t 求解以上两个方程得到常数K1=3和K2=4,得到电容电 压和电感电流的零输入响应: 0.04e [7cos( ) 24sin( )] e cos( 73.74 )A ( 0) d d ( ) ( ) e [3cos 4sin( )] 5e cos( 53.1 )V ( 0) c L c = = − = + = + = − − − − − t t t t t u i t C u t t t t t t t t t 4 4 4 4 4 4 3 3 3 3 将两个不相等的固有频率 s1 =-3+j4 和 s2 =-3-j4 代入式 (9-11)得到 ( ) e [ cos sin( )] ( 0) C = 1 + 2 − u t K t K t t t 4 4 3
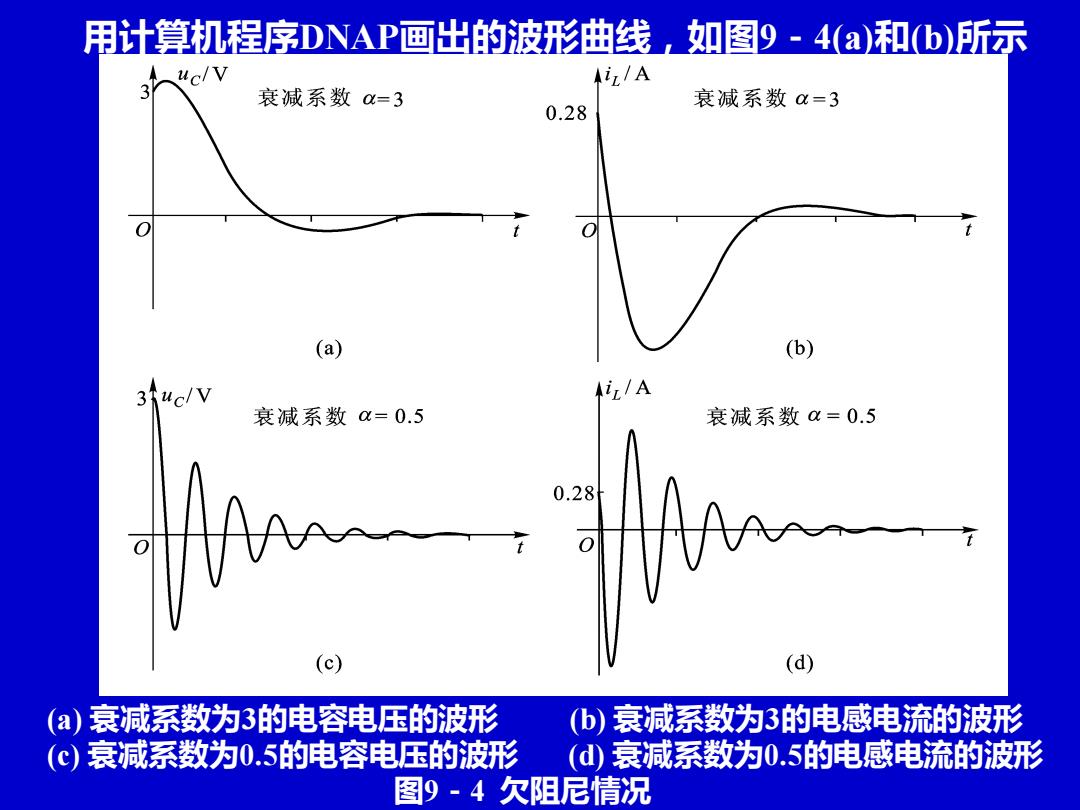
用计算机程序DNAP画出的波形曲线,如图9-4(a)和b)所示 AiL/A 衰减系数=3 衰减系数a=3 0.28 (a) (b) 3 uc/V AiL/A 衰减系数a=0.5 衰减系数a=0.5 .28 (c) (d) (a)衰减系数为3的电容电压的波形 (b)衰减系数为3的电感电流的波形 (c)衰减系数为0.5的电容电压的波形 (d)衰减系数为0.5的电感电流的波形 图9-4欠阻尼情况
用计算机程序DNAP画出的波形曲线,如图9-4(a)和(b)所示 (a) 衰减系数为3的电容电压的波形 (b) 衰减系数为3的电感电流的波形 (c) 衰减系数为0.5的电容电压的波形 (d) 衰减系数为0.5的电感电流的波形 图9-4 欠阻尼情况

从式(9-11)和图9-4波形曲线可以看出,欠阻尼情况的 特点是能量在电容与电感之间交换,形成衰减振荡。电阻 越小,单位时间消耗能量越少,曲线衰减越慢。 当例9-3中电阻由R=62减小到R=12,衰减系数由3变 为0.5时,用计算机程序DNAP得到的电容电压和电感电流 的波形曲线,如图9-4(©)和(d)所示,由此可以看出曲线衰 减明显变慢。 假如电阻等于零,使衰减系数为零时,电容 电压和电感电流将形成无衰减的等幅振荡
从式(9-11)和图9-4波形曲线可以看出,欠阻尼情况的 特点是能量在电容与电感之间交换,形成衰减振荡。电阻 越小,单位时间消耗能量越少,曲线衰减越慢。 当例9-3中电阻由R=6Ω减小到R=1Ω,衰减系数由3变 为0.5时,用计算机程序DNAP得到的电容电压和电感电流 的波形曲线,如图9-4(c)和(d)所示,由此可以看出曲线衰 减明显变慢。假如电阻等于零,使衰减系数为零时,电容 电压和电感电流将形成无衰减的等幅振荡