
回归方程 ·从样本数据出发,建立的样本回归方 程 Y (hat)=bo+bx1+b2 x2 +.+bmXm Y(hat):xi,2.xm的估计值 ·b0,b1rb2,.,bm:参数 Bo,Bp.,B的估计值,即常数项和偏 回归系数
回归方程 • 从样本数据出发,建立的样本回归方 程 Y(hat)=b0+b1x1+b2 x2 +.+bmxm Y(hat): μY|x1, x2.xm的估计值 • b0 ,b1,b2,.,bm:参数 β0 ,β1, . ,βm的估计值,即常数项和偏 回归系数

回归方程的建立 参数估计原理 ·根据最小二乘法原理,通过对微分方程组 求偏导数,解出常数项b。(或待定系数) 和偏回归系数b1,b2.bm ·最小二乘法原理 使得实际观察值Y与回归方程 的估计值Y(hat)之间的残差平方和最小
回归方程的建立 参数估计原理 • 根据最小二乘法原理,通过对微分方程组 求偏导数,解出常数项b0 (或待定系数) 和偏回归系数b1,b2.bm。 • 最小二乘法原理 使得实际观察值Yi与回归方程 的估计值Y(hat)之间的残差平方和最小

正规方程矩阵形式与解的矩阵形式 XXB-XY B=(YXXY B为方程的解
正规方程矩阵形式与解的矩阵形式 B X X X Y X XB X Y = = −1 ( ) B为方程的解
·B=(X'X)1XY中 厂1X11X12.X1m X= 1X21X22.X2m Y= B= b 1 Xn1 Xn2 .Xnm2
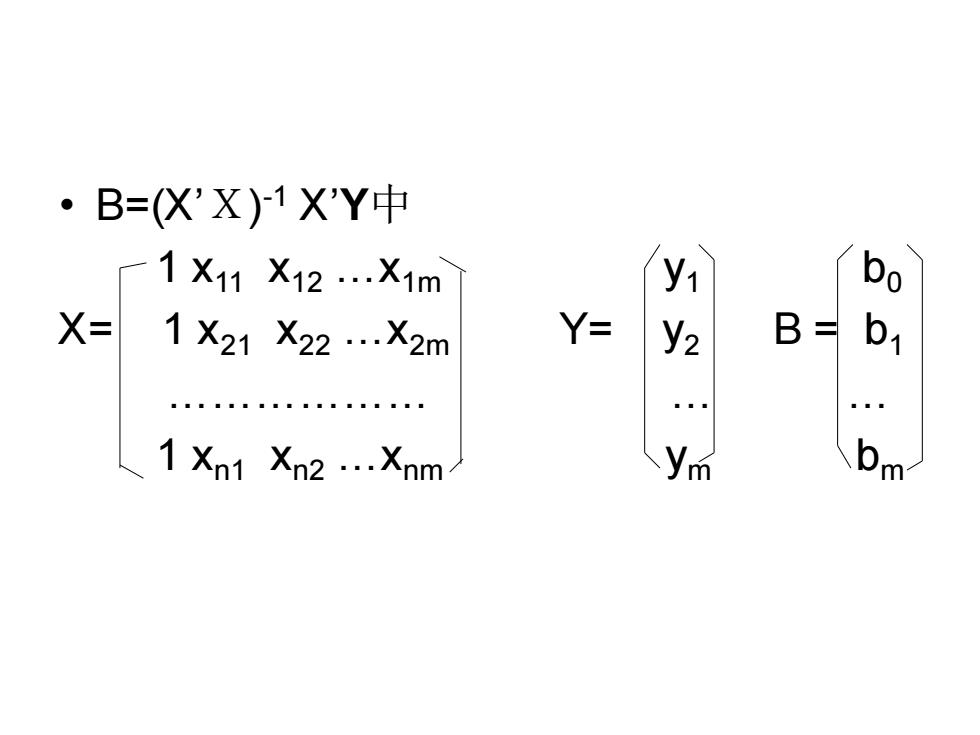
• B=(X’X) -1 X’Y中 1 x11 x12 .x1m y1 b0 X= 1 x21 x22 .x2m Y= y2 B = b1 . . . 1 xn1 xn2 .xnm ym bm

回归效果的检验 ·建立了回归方程后,需要进行假设性检验 整个模型的假设检验 各回归参数的假设检验
回归效果的检验 • 建立了回归方程后,需要进行假设性检验 整个模型的假设检验 各回归参数的假设检验