《医学统计学》课程教学课件（PPT讲稿）第一部份 基本统计（相关与回归）

线性相关 (linear correlation) 主讲教师 钟晓妮副教授

主讲教师 钟晓妮副教授

线性相关分析： 是在(X,Y)服从正态分布（双变量正态分布）的 假定下，用线性相关的统计分析方法研究两变量间 数量变化关系的密切程度和方向，称为线性相关分 析

线性相关分析： 是在（X，Y）服从正态分布（双变量正态分布）的 假定下，用线性相关的统计分析方法研究两变量间 数量变化关系的密切程度和方向，称为线性相关分 析

X~N(4,o),Y~N(4,O,) 标准化变量 U=水-4 V= Y-Hy 0x 0y 则X与Y的相关系数 p==承X1于 -1≤p≤1

~ ( , ) X N  x  x ， ~ ( , ) Y N  y  y 标准化变量 x X x U  −  = ， y Y y V  −  = 则 X 与 Y 的相关系数 X Y X Y Y Y X X X Y E UV E         = − − = ( ) = [( )( )] − 1    1

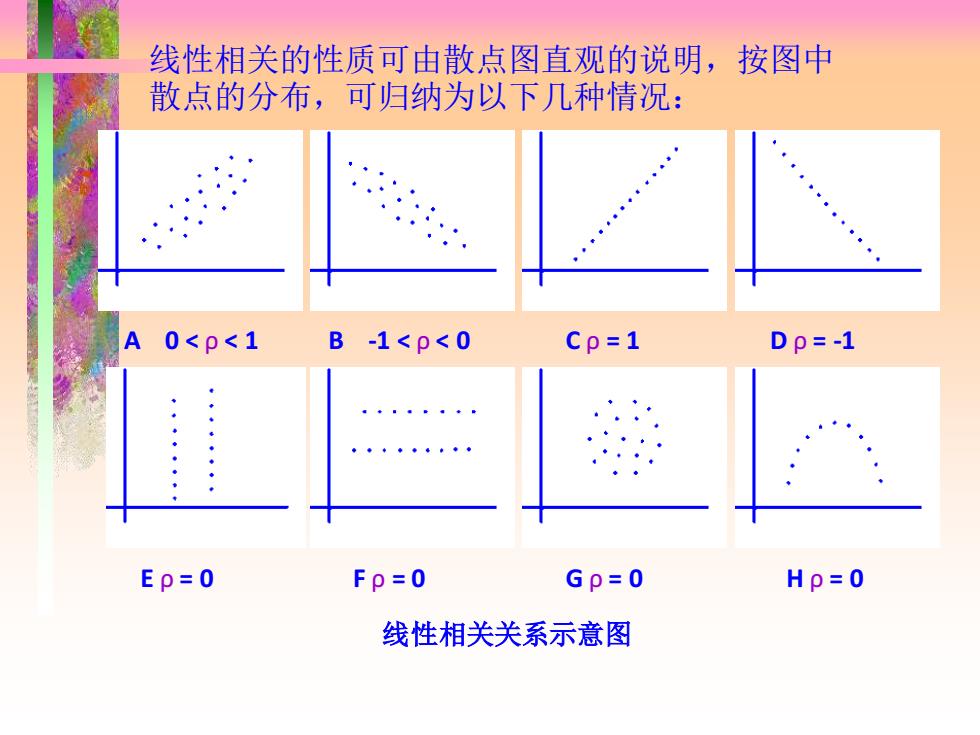
线性相关的性质可由散点图直观的说明，按图中 散点的分布，可归纳为以下几种情况： A 0<p<1 B-1<p<0 Cp=1 Dp=-1 ··. 年0◆◆多·。 Ep=0 Fp=0 Gp=0 Hp=0 线性相关关系示意图

线性相关的性质可由散点图直观的说明，按图中 散点的分布，可归纳为以下几种情况： A 0 < ρ < 1 E ρ = 0 B -1 < ρ < 0 C ρ = 1 D ρ = -1 F ρ = 0 G ρ = 0 H ρ = 0 线性相关关系示意图

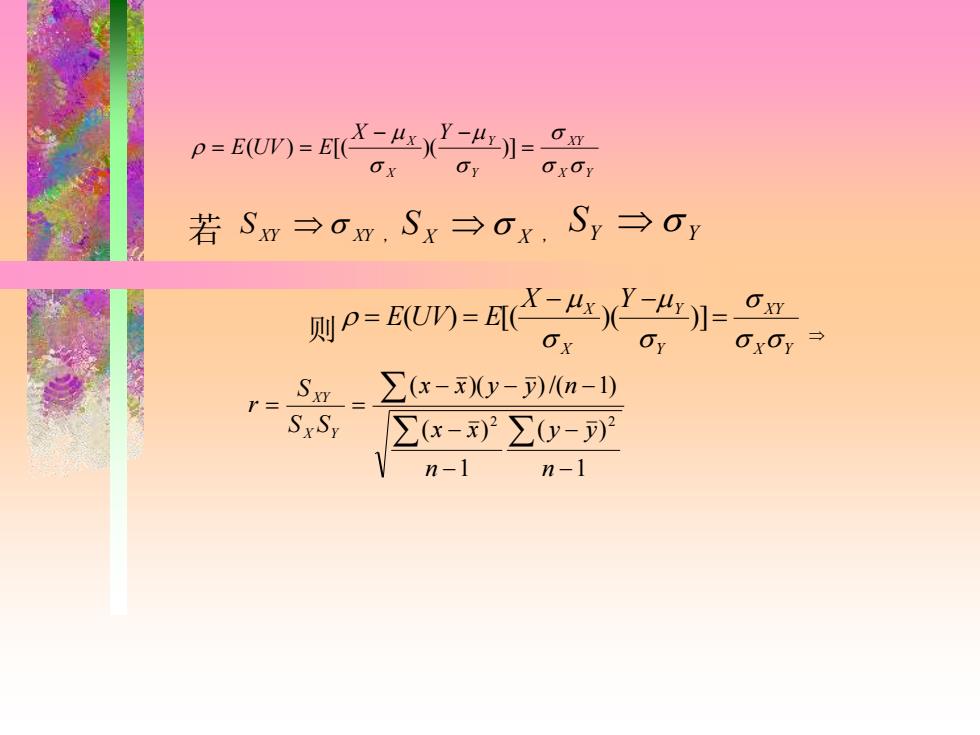
p=EUm=X-LXY-4】=ag OxOY 若Sw→om.Sx→ox.Sy→oy 则P=U=A二4X刀= OX Sm=∑x-x0y-)n-) SxSy ∑x-)2∑0y-列 n-1 n-1

X Y XY Y Y X X X Y E UV E         = − − = ( ) = [ ( )( )] 若 S XY   XY ， X X S   ， SY   Y 则 X Y X Y Y Y X X X Y E UV E         = − − = ( ) = [( )( )]  1 ( ) 1 ( ) ( )( )/( 1) 2 2 − − − − − − − = =    n y y n x x x x y y n S S S r X Y X Y