
正态分布 1、图形 2、特征 3、面积 4、应用
正态分布 1、图形 2、特征 3、面积 4、应用
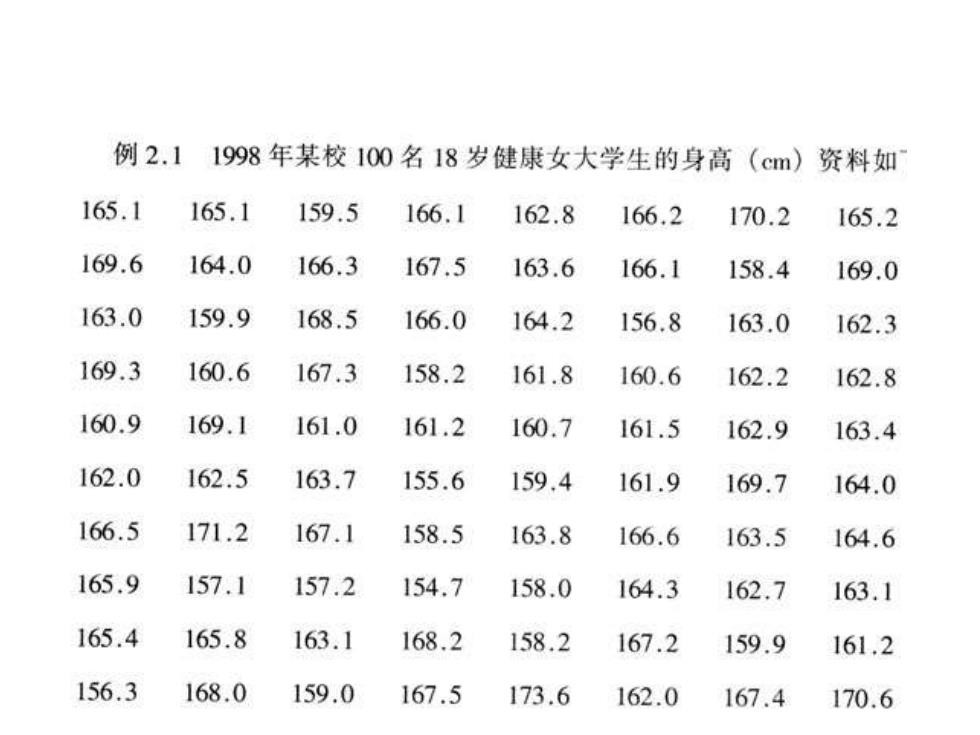
例2.11998年某校100名18岁健康女大学生的身高(cm)资料如 165.1 165.1 159.5 166.1 162.8 166.2 170.2 165.2 169.6 164.0 166.3 167.5 163.6 166.1 158.4 169.0 163.0 159.9 168.5 166.0 164.2 156.8 163.0 162.3 169.3 160.6 167.3 158.2 161.8 160.6 162.2 162.8 160.9 169.1 161.0 161.2 160.7 161.5 162.9 163.4 162.0 162.5 163.7 155.6 159.4 161.9 169.7 164.0 166.5 171.2 167.1 158.5 163.8 166.6 163.5 164.6 165.9 157.1 157.2 154,7 158.0 164.3 162.7 163.1 165.4 165.8 163.1 168.2 158.2 167.2 159.9 161.2 156.3 168.0 159.0 167.5 173.6 162.0 167.4 170.6
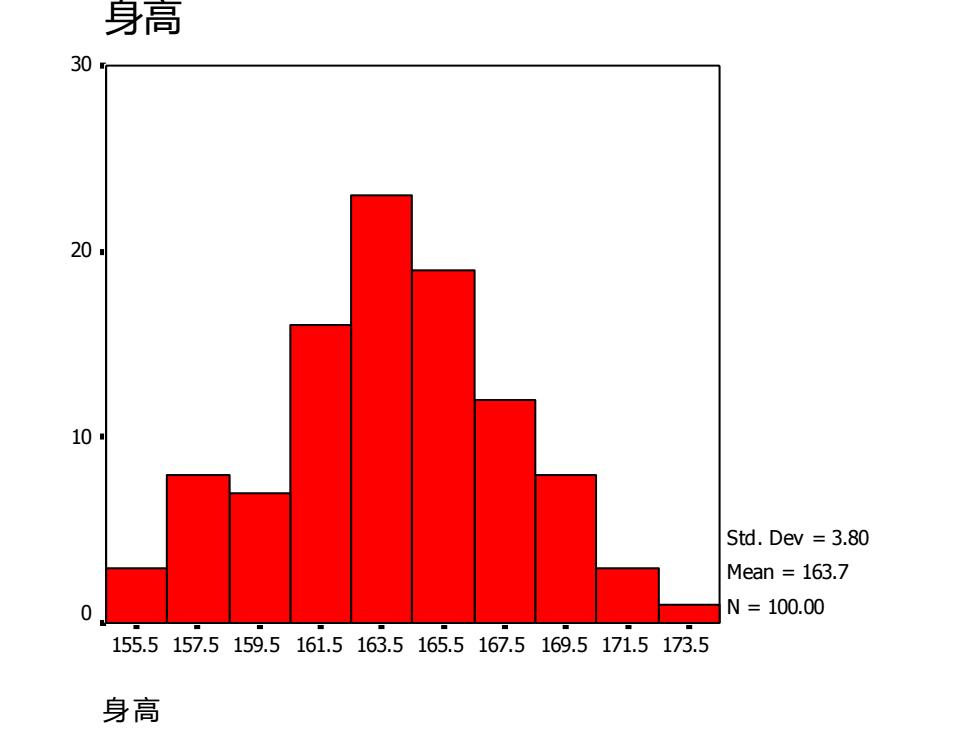
身高 30 20 10: Std.Dev =3.80 Mean=163.7 0 N=100.00 155.5157.5159.5161.5163.5165.5167.5169.5171.5173.5 身高
? ? 155.5 157.5 159.5 161.5 163.5 165.5 167.5 169.5 171.5 173.5 ? ? Frequency 30 20 10 0 Std. Dev = 3.80 Mean = 163.7 N = 100.00 身 高 155.5 157.5 159.5 161.5 163.5 165.5 167.5 169.5 171.5 173.5 身高 Frequency 30 20 10 0 Std. Dev = 3.80 Mean = 163.7 N = 100.00
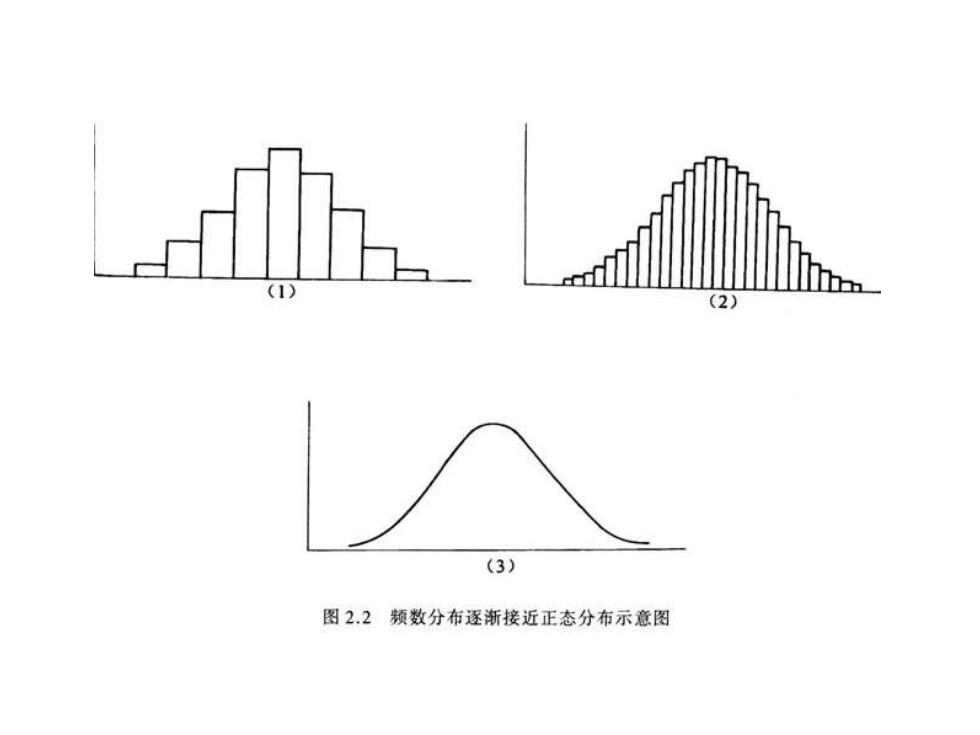
(1) (2) (3) 图2.2颜数分布逐渐接近正态分布示意图

正态分布的特征 均数处最高; 关于x=u对称; 2个参数N(u,o) 标准正态分布N(0,1); 标准正态变换(变换公式) 曲线下的面积有一定规律
正态分布的特征 均数处最高; 关于x=μ对称; 2个参数 N(u ,) 标准正态分布:N(0 ,1); 标准正态变换(变换公式); 曲线下的面积有一定规律