
第八章 单向方差分析 One way analysis of variance 主讲教师 田考聪教授
第八章 单向方差分析 One way analysis of variance 主讲教师 田考聪教授

一、问题的提出 先看一个例子: 某医生为研究一种降糖药的疗效,以统一 的纳入标准和排除标准选择了39名11型糖尿病 患者,随机将其分为两组进行双盲临床试验。 其中试验组19人,对照组20人,对照组服用公 认的降糖药物。治疗4周后测得其餐后2小时血 糖的下降值(mo1/L),结果如表1。问治疗4周 后餐后2小时血糖下降值的两组总体水平是否 不同?
一、问题的提出 先看一个例子: 某医生为研究一种降糖药的疗效,以统一 的纳入标准和排除标准选择了39名II型糖尿病 患者,随机将其分为两组进行双盲临床试验。 其中试验组19人,对照组20人,对照组服用公 认的降糖药物。治疗4周后测得其餐后2小时血 糖的下降值(mmol/L),结果如表1。问治疗4周 后餐后2小时血糖下降值的两组总体水平是否 不同?
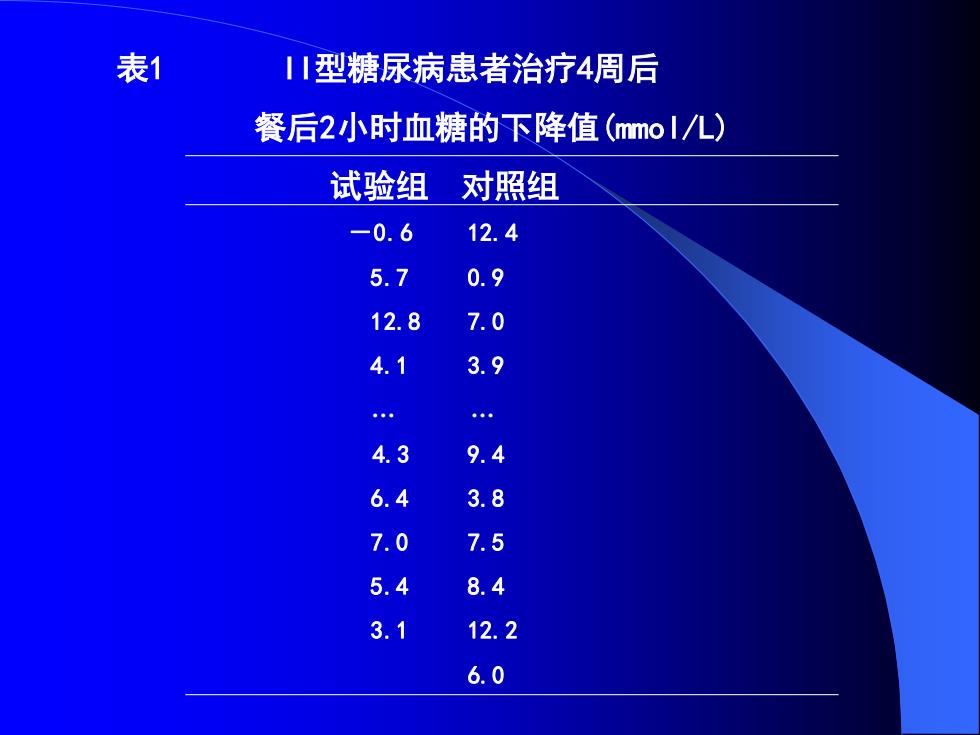
表1 11型糖尿病患者治疗4周后 餐后2小时血糖的下降值(mol/L) 试验组对照组 一0.6 12.4 5.7 0.9 12.8 7.0 4.1 3.9 4.3 9.4 6.4 3.8 7.0 7.5 5.4 8.4 3.1 12.2 6.0
表1 II型糖尿病患者治疗4周后 餐后2小时血糖的下降值(mmol/L) 试验组 对照组 -0.6 12.4 5.7 0.9 12.8 7.0 4.1 3.9 . . 4.3 9.4 6.4 3.8 7.0 7.5 5.4 8.4 3.1 12.2 6.0

显然,当两个样本来自正态总体,且两个 总体方差相等时,我们可用两样本均数比较的 t一检验来解决这个问题。其检验假设:为 H4=4 H4≠ 其检验统计量为: x1-X2 其中: Sx-X (n-1)S2+(h2-1)S n1+n2-2
显然,当两个样本来自正态总体,且两个 总体方差相等时,我们可用两样本均数比较的 t-检验来解决这个问题。其检验假设:为 0 1 2 1 1 2 H H : : = 1 2 1 2 X X X X t S − − = 1 2 2 2 2 2 1 1 2 2 1 2 1 2 1 1 ( 1) ( 1) , 2 X X c c n S n S S S S n n n n − − + − = + = + − 其检验统计量为: 其中:

但在实际工作中,常常会遇到两个 以上的样本均数的比较,如将上述问题 改为: 某医生为研究一种降糖药的疗效, 以统一的纳入标准和排除标准选择了60 名11型糖尿病患者,随机将其分为三组 进行双盲临床试验。其中高剂量组21人, 低剂量组19人,对照组20人,对照组服 用公认的降糖药物。治疗4周后测得其餐 后2小时血糖的下降值(mol/儿),结果如 表2。问治疗4周后餐后2小时血糖下降值 的三组总体水平是否不同?
但在实际工作中,常常会遇到两个 以上的样本均数的比较,如将上述问题 改为: 某医生为研究一种降糖药的疗效, 以统一的纳入标准和排除标准选择了60 名II型糖尿病患者,随机将其分为三组 进行双盲临床试验。其中高剂量组21人, 低剂量组19人,对照组20人,对照组服 用公认的降糖药物。治疗4周后测得其餐 后2小时血糖的下降值(mmol/L),结果如 表2。问治疗4周后餐后2小时血糖下降值 的三组总体水平是否不同?