西安电子科技大学：《电路分析基础》课程教学资源（PPT课件）第六章 二端口电路

第六章二端口电路 划分通常以子电路的作用而定。例如上面的N1可以是信号 源，而N2可以是负载，N3则是一个连接激励和负载的双口电路。 N3 U2 N N2

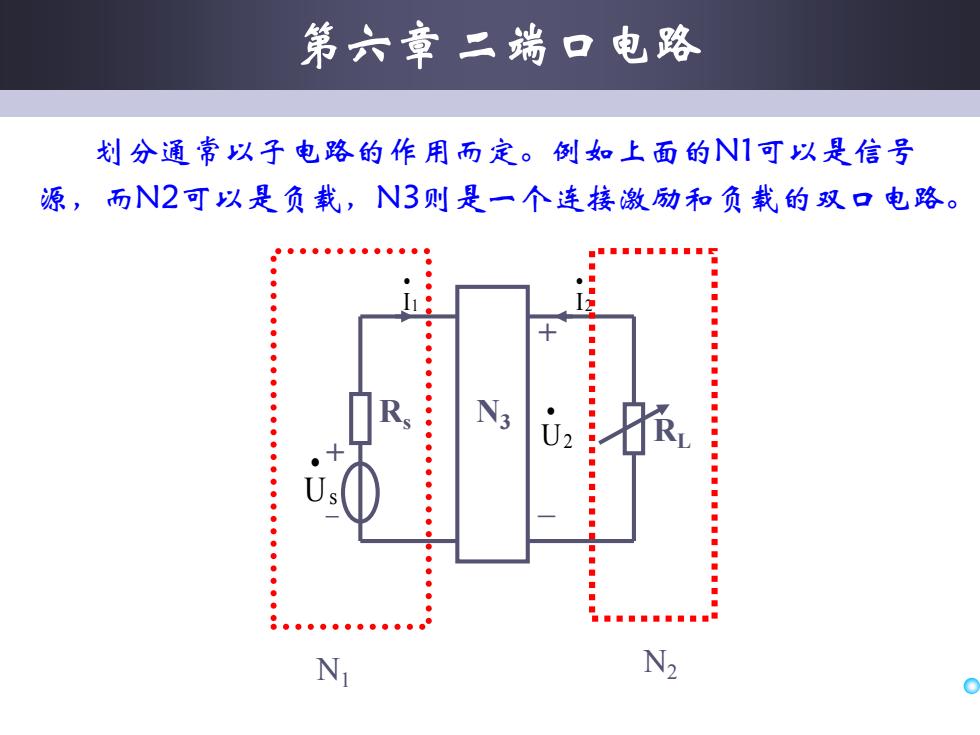
划分通常以子电路的作用而定。例如上面的N1可以是信号 源，而N2可以是负载，N3则是一个连接激励和负载的双口电路。 RL I2 • + _ U2 N • 3 I1 • Rs + _ Us • N1 N2

第六章二端口电路 对整个网络进行划分，可以根据子网络的不同性质（非 线性，动态电路，含源电路等等)分别进行研究分析，并带来 很大方便。 划分后我们感兴趣的往往是双口电路端口的电压、电流关 系而不再对道路、内部的压流分配感兴趣了，因此实际上解决 的是双口网络的VCR问题。（单口网络的VCR可以用戴维南定 理来表述)

对整个网络进行划分，可以根据子网络的不同性质（非 线性，动态电路，含源电路等等）分 别进行研究分析，并带来 很大方便。 划分后我们感兴趣的往往是双口电路端口的电压、电流关 系而不再对道路、内部的压流分配感兴趣了，因此实际上解决 的是双口网络的VCR问题。（单口网络的VCR可以用戴维南定 理来表述）

第六章二端口电路 i R N 白R 9 该双口电路N就起连接负载和信号源的作用，其对外端的作 用体现在： ● U1,I1和U2,I2 因此这四个量是我们研究的重点对象

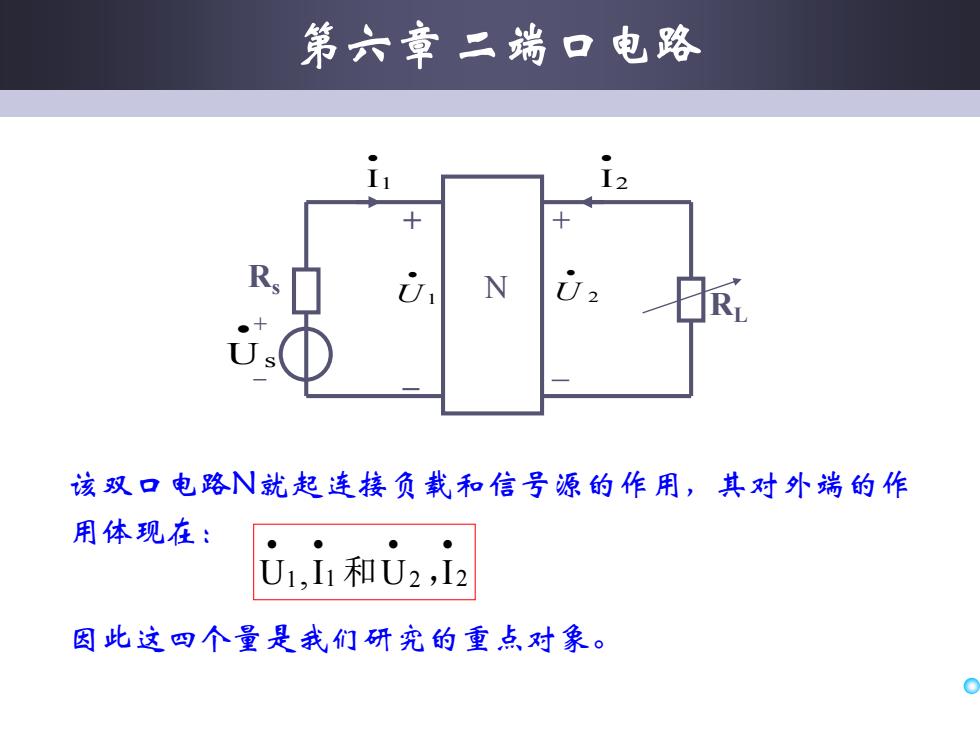
该双口电路N就起连接负载和信号源的作用，其对外端的作 用体现在： U1,I1 U2 I2 • • • • 和 ， 因此这四个量是我们研究的重点对象。 RL I2 • + _ 2 • N U I1 • Rs + _ Us • + _ 1 • U

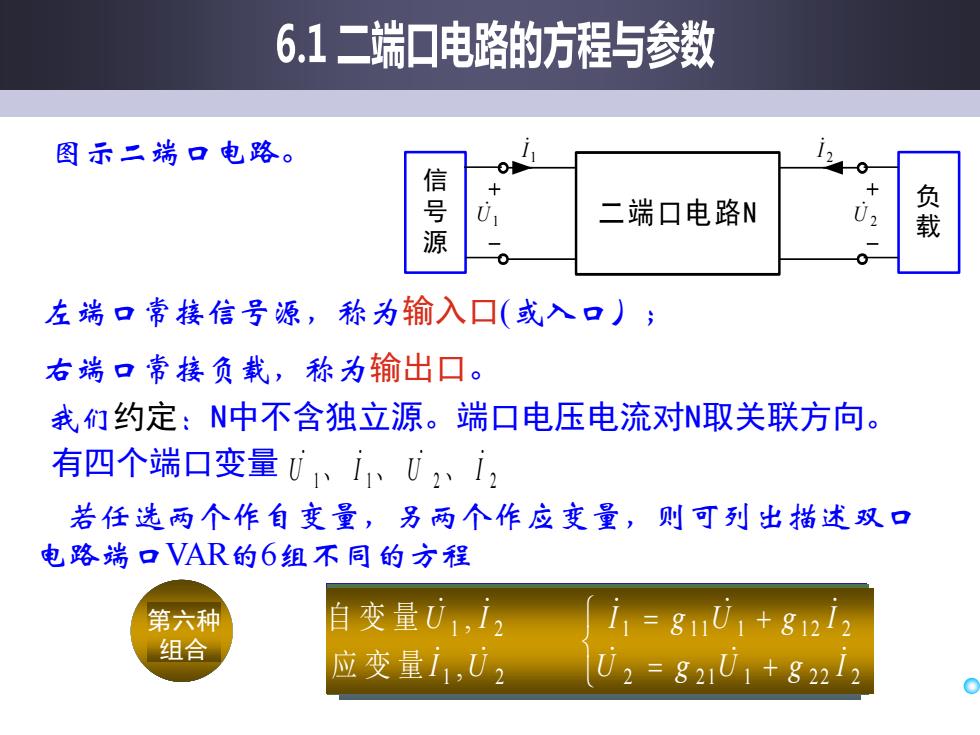
6.1二端口电路的方程与参数 图示二端口电路。 20 信号源 + 二端口电路N 02 载 左端口常接信号源，称为输入口（或入口）； 右端口常接负载，称为输出口。 我们约定：N中不含独立源。端口电压电流对N取关联方向。 有四个端口变量U、i、U,、i, 若任选两个作自变量，另两个作应变量，则可列出描述双口 电路端口VAR的6组不同的方程 第六种 自变量01,12 11=g1U1+8122 组合 应变量i1,0) U2=821U1+g2212

   = + = + 2 2 1 1 2 2 2 1 1 1 1 1 2 2 1 2 1 2 , , U z I z I U z I z I U U I I           应变量 自变量    = + = + 2 2 1 1 2 2 2 1 1 1 1 1 2 2 1 2 1 2 , , I y U y U I y U y U I I U U           应变量 自变量    = + − = + − ( ) ( ) , , 1 2 1 2 2 2 2 1 1 1 2 1 2 2 1 1 2 2 I a U a I U a U a I U I U I           应 变 量 自 变 量    = + − = + − ( ) ( ) , , 2 2 1 1 2 2 1 2 1 1 1 1 2 1 2 2 1 1 I b U b I U b U b I U I U I           应变量 自变量    = + = + 2 2 1 1 2 2 2 1 1 1 1 1 2 2 1 2 1 2 , , I h I h U U h I h U U I I U           应变量 自变量    = + = + 2 2 1 1 2 2 2 1 1 1 1 1 2 2 1 2 1 2 , , U g U g I I g U g I I U U I           应变量 自变量 U1 二端口电路N  U 2  1 I  2 I  信 号 源 负 载 左端口常接信号源，称为输入口(或入口）； 右端口常接负载，称为输出口。 我们约定：N中不含独立源。端口电压电流对N取关联方向。 有四个端口变量 1 1 2 2 U I U I  、  、  、  若任选两个作自变量，另两个作应变量，则可列出描述双口 电路端口VAR的6组不同的方程 第一种 组合 第二种三四五六 图示二端口电路

6.1二端口电路的方程与参数 一、开路参数和短路参数 1、开路参数 (1)Z方程 选和1为自变量，以U 和U,为应变量描述端口 二端口电路N VAR,为此，端口外加 电流源。 由叠加原理有 01=11i1+12i2 称二端口电路N的 Z方程 02=z21i1+z2i2 Z11、Z12、 Z21、Z22称Z参数。乙方程写成矩阵形式 矩阵Z= 211 212 称为Z矩阵。 z21 22

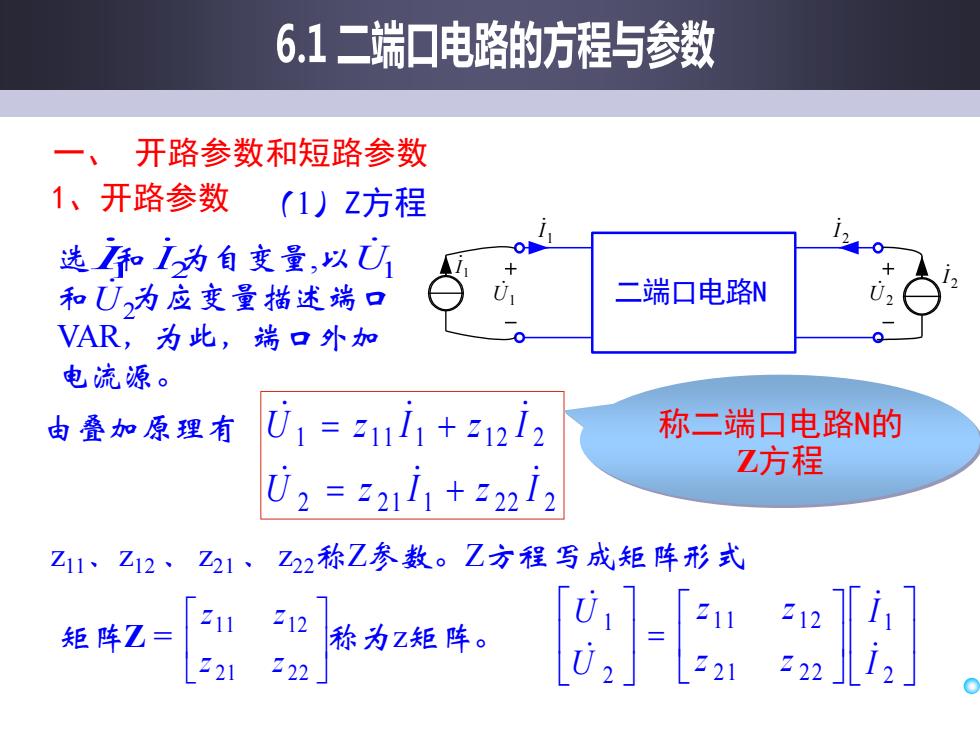
一、 开路参数和短路参数 1、开路参数 U1 二端口电路N  U2  1 I  2 I  1 I  2 I 选 和 为自变量  ,以 和 为应变量描述端口 VAR，为此，端口外加 电流源。 I 1  2 I  U1  U2  由叠加原理有 2 2 1 1 2 2 2 1 1 1 1 1 2 2 U z I z I U z I z I       = + = + 称二端口电路N的 Z方程 z11、z12 、z21 、z22称Z参数。Z方程写成矩阵形式              =      2 1 2 1 2 2 1 1 1 2 2 1 I I z z z z U U     矩阵Z =  称为z矩阵。      21 22 11 12 z z z z （1）Z方程