
一、抽样误差基本概念 中样误并只抽样推断中的一个承要概今,它是指山干销机抽样的偶然因素伸样本各单品 结构不足以代表总体各单位结构,从而引起样本指标与总体指标之间的绝对离差,用数学符 号可表示为斥-或p-P川 在抽样调查过程中,用抽样指标来代表总体指标进行必要的推算,必然会产生误差问题。 因为抽样指标山于种种原因,不会与总体指标完全一样,它们两者之间往往不会完全相等, 抽样半均数或抽样成数与总体平均数或总体成数之侧仕往会产生一定的误差。抽样误差越 小,表示样本的代表性越高:反之,抽样误差越大,样本的代表性越低。 1、抽样误差的种类 在抽样调查过程中会产生两类误差,即登记性误差与代表性误差,代表性误差又可分为 系统性误第和偶然性误差 登记性误差是指在统计调查、整理或计算过程中,山于主客观原因影响而产生的误差 这种误差 “切统登中有可论 产生,但登记性误差可以通过提高调查人员的思想素质 和业务水平,改进调查方法和组织工作,建立严格的工作责任制训以避免,属于可避免的误 差。 代表性误差是山于调查过程中以部分来代表总体时,山于代表性不是或不完全而产生的 误差,根据其成因可分为两种,即系统性误差和随机误差。系统性误差是山于没有严格遵守 站机原则而产生的误差 ,如在抽样调查抽取调查单位 调查者没有 亚格遵 守随机原则,而 是有意识地挑选较好或较坏的单位进行调查,山此导致样本的代表性降低,据此计算的抽样 指标数值必然比总体指标数值偏高或偏低,从而产生的误差。系统误差也属于可避免的误差。 随机误差则是指在抽选样本过程中,虽然严格遵守随机原则,但山于样本的非均匀性,可能 油到各种不同的样本,只要样本的结物与总体比有出入,就会出现误。随机误是样 查本身所固有的 是不可避免的 种偶然性的代表性误差。抽样调查中能够计算并加以 控制的就是这种随机误 。以下课程介绍与处理的均指随机误差 2、影响抽样误差的因素 影响抽样误差的主要因素有以下几方面: (1)抽样单位数目的多少 ,在其他条件不变的情况下,抽样单位数越少,抽样误差越大:反之,抽样单位数越多, 如果样本单位数 等于总体单位数N,即样本等于总体时,抽样调查也就等 于全面调查,也就不存在抽样误差 (2)总体各单位标志变异程度 在其他条件不变的情况下,总体单位标志变异程度越小,抽样误差也就越小:反之,总 体单位标志变异程度越大,抽样误差就越大。如果总体各单位标志值相等,则抽样误差为零 面将会通过公式了解到, 抽样误差的变动与总体各单位标志变异程度的大小成正比例关 系 (3)抽样调查的组织形式 抽样调查按组织方式,可分为简单随机抽样、等距抽样、类型抽样和整群抽样。每一种 抽样调查的抽样误差都是不相同的。一般而言,类型抽样的样本代表性较高,等距抽样次之, 而简单随机抽样和整群抽样误差较大。本章第四节将分析各种抽样调查组织方式的误差 (4)抽样方法 抽样的方法不同,抽样误差也不同,一般而言,重复抽样的抽样误差比不重复抽样的抽 样误差要大些。 二、抽样的平均误差
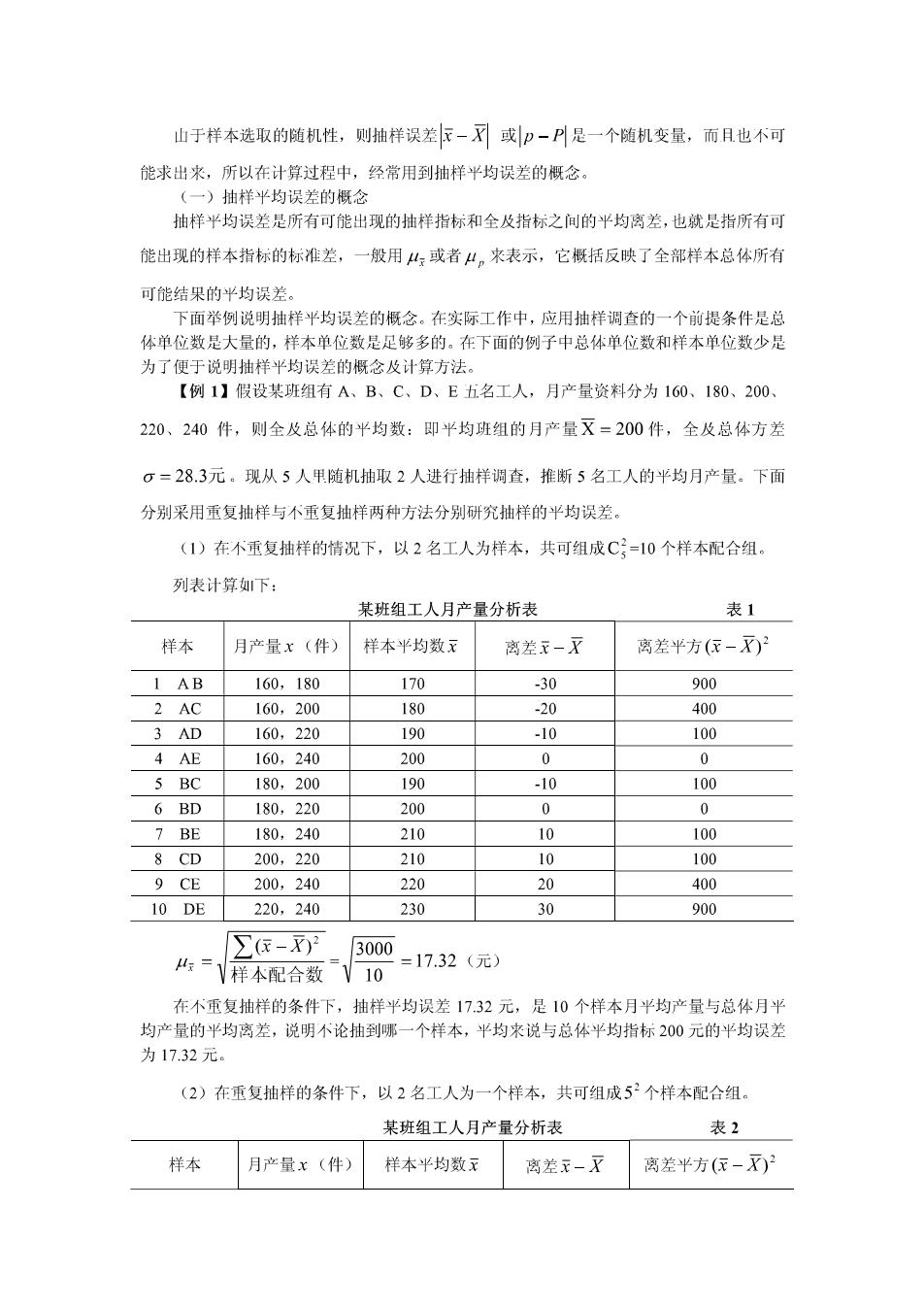
山于样本选取的随机性,则抽样误差下-或p一P是一个随机变量,而日也不可 能求出来,所以在计算过程中,经常用到抽样平均误差的概念 )抽样平均误差的概念 抽样平均误差是所有可能出现的抽样指标和全及指标之间的平均离差,也就是指所有可 能出现的样本指标的标准差,一般用4:或者4。米表示,它概括反映了全部样本总体所有 可能结果的平均误差。 面举例说明抽样平均误差的概念。在实际工作中,应用抽样调查的一个前提条件是总 体单位数是大量的,样本单位数足足够多的。在下面的例子中总体单位数和样本单位数少是 为了便于说明挂样平均误差的慨念及计算方法。 【例1】假设某班组有A、B、C、D、E五名工人,月产量资料分为160、180、200、 220、240件,则全及总体的平均数:即Ψ均班组的月产量=200件,全及总体方若 。=28.3元,现从5人甲随机抽取2人进行抽样调查,推断5名工人的半均月产量。下面 分别采用玉复抽样与不重复抽样两种方法分别研究抽样的平均误差。 (1)在不重复抽样的情况下,以2名工人为样本,共可组成C:=10个样本配合组。 列表计算如下: 某班组工人月产量分析表 表1 样本 月产量x(件) 样本平均数元 离差元- 离差Ψ方(依-)2 1 AB 160,180 170 -30 900 2 AC 160,200 180 -20 400 3 AD 160.220 190 -10 100 4 AE 160.240 200 0 0 5 BC 180,200 190 -10 100 6 BD 180,220 200 0 0 7 BE 180,240 210 10 100 8 CD 200.220 210 10 100 9 CE 200,240 229 400 10 DE 220,240 2530 30 900 ∑(-) 3000 4=样本配合数10 =17.32(元》 在不重复抽样的条件下,抽样平均误差17.32元,是10个样本月平均产量与总体月半 均产量的平均离差,说明不论抽到啸一个样本,平均来说与总体平均指标200元的平均误差 为17.32元。 (2)在重复抽样的条件下,以2名工人为一个样本,共可组成52个样本配合组。 某班组工人月产量分析表 表2 样本 月产量x(件) 样本平均数 离若元一X 离差平方(低-月
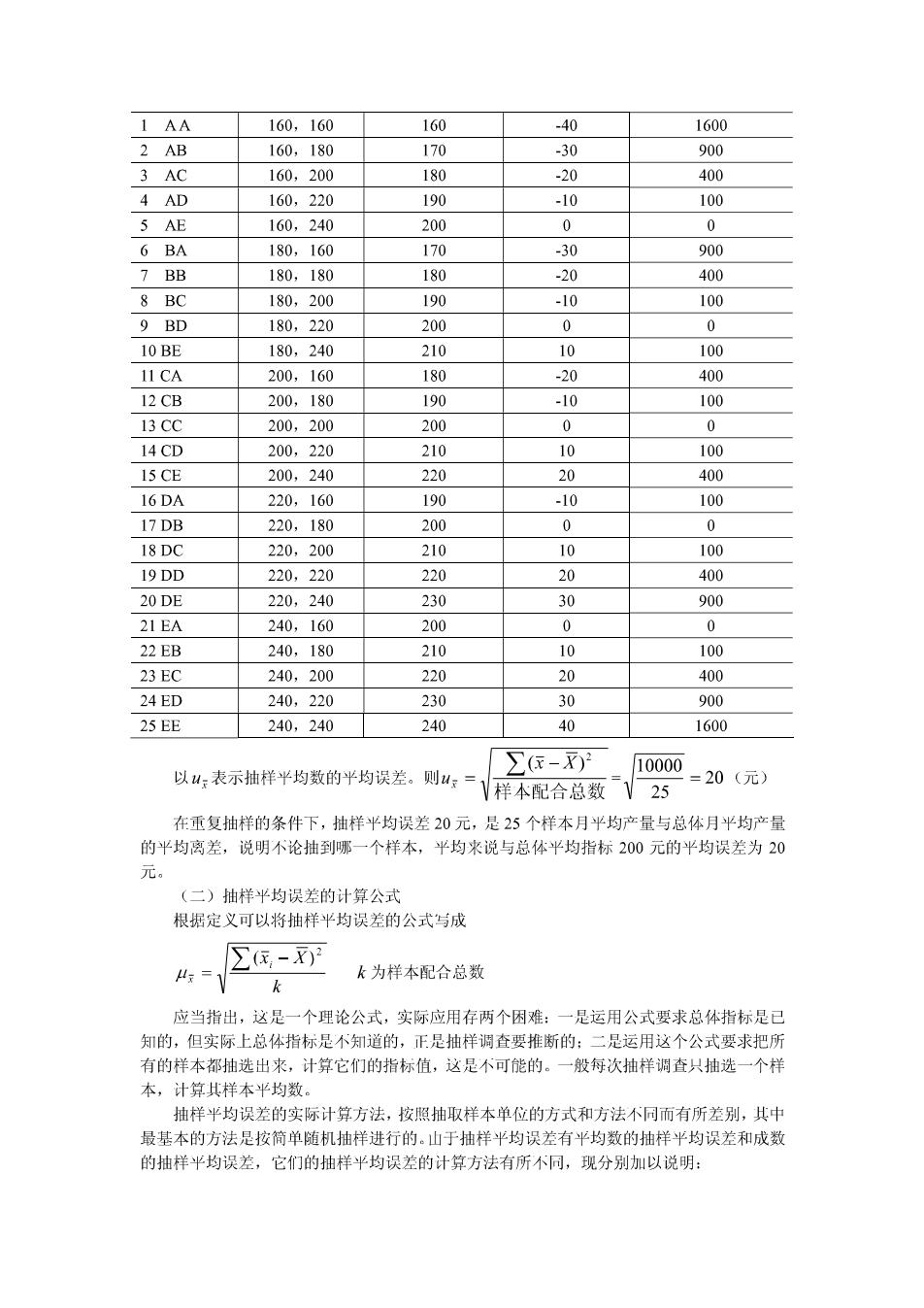
1 AA 160.160 160 .40 1600 2 AB 160,180 170 900 3A0 160,200 180 -20 400 4 AD 160.220 190 -10 100 5 AE 160.240 200 6 BA 180,160 170 900 7 BB 180,180 180 -20 400 8 BC 180.200 190 -10 100 9 BD 180.220 200 0 10B 180,240 210 11CA 200,160 180 -20 400 12CB 200.180 190 -10 100 200.200 200 0 0 200,220 210 10 100 15 CE 200,240 220 20 400 16DA 220.160 190 .10 100 17DB 220.180 200 0 220,200 210 0 100 19DD 220,220 220 20 400 20DE 220.240 230 30 900 21EA 240.160 200 0 240,180 210 100 23 EC 240,200 220 20 400 245D 240.220 230 30 900 25 EE 240,240 240 40 1600 ∑(- 以山,表示抽样平均数的平均误差.则“:=样本配合总数25 10000 =20(元) 在重复抽样的条件下,抽样Ψ均误差20元,是25个样本月Ψ均产量与总体月Ψ均产量 的平均离差,说明不论抽到哪一个样本,平均来说与总体平均指标200元的平均误差为20 (二)抽样平均误差的计算公式 根据定义可以将抽样平均误差的公式写成 ∑保,- := k为样本配合总数 应当指出,这是一个理论公式,实际应用存两个困难:一是运用公式要求总体指标是已 知的,但实际上总体指标是不道的,正是抽样调查要推断的:二是运用这个公式要求把所 有的样本都抽选出来,计算它们的指标值,这是不可能的。一般每次抽样训查只抽选一个样 本,计算此样本毕均数。 抽样平均误差的实际计算方法,按照抽取样本单位的方式和方法不同而有所差别,其中 最基本的方法是按简单随机抽样进行的。山于抽样平均误差有平均数的抽样平均误差和成数 的抽样平均误差,它们的抽样半均误差的计算方法有所不同,现分别加以说明:

1、抽样平均数的抽样平均误差 以以,表示抽样半均数的平均误差,。表示总体的标准差。根据定义得: 4:'=E元-E(x=E(依-) -西+名+x+A+x-F+双+F+A+天 =-万+(-万+化-+Λ+.-X (1)玉复抽样抽样平均数的抽样平均误差。在重复抽样的情况下,这时样本变量 x,x,x,人,x是相互独立的,样本变量x与总体变量X同分布,展开上式得 4=B-+E,-万+AE.-+∑E-X-X列 -Ex-+Ex-+A+Ex-X为 ( 上式表阴样Y约的Y约误坐仪为全收总秋福差的石·例如当样太华位数为 ,则半均误差仪为总体标准差的合这说明。,一个总体的某一标志的安动度可能很大 但抽到若干单位加以平均之后,抽样平均数的标准差比总体的标准差大大地箱小了。所以, 抽样平均数作为估计量是史有效的。从上式还可以看出,抽样平均误差和总体标志变动度的 大小成正比,而和样本单位的平方根成反比。例,抽样平均误差要减少,则样本单位 数必须增大到4信:抽样半均误差要减少为原来的},则样本数要扩大到原来的9倍等。 (2)不重复抽样的抽样误差 在不重复抽样的情况下,这时样本变量,x,xAx,不是相互独立。展开上式得 4=E-+E-+AE,-X+∑E-Xe-X列 示之(-形+王-,一刀(你过程路

果司 在总体单位数N很大的情况下,可以近似的表示为: 从上述过程可以看出,不重复抽样平均方差等于重复抽样平均方差乘以校正因子 小-号·式足大于0面于1的流云系上这个小杆1的正数。多然小于来的威。 所以,不重复抽样半均误差的数值一定小于重复抽样的抽样平均误差。也就是说,抽样的方 法对挂件的联差是有影的:在一复指视下,总体单位数限大,曲样北制丹很小,则小-只 接近于1,因此, -月与云运,核季工中,极有送水8验 情况下或者总体单位数N很大时,一般均用重复抽样半均误差公式来计算个重复抽样的半 均误差。 2、抽样成数的抽样平均误差 在掌握抽样平均数的平均误差公式的基础上,再来求抽样成数的平均误差公式是比较简 单的。只须将全及成数的标准差平方代替公式中的全及平均数的标准差的平方,就可以得到 抽样成数的平均误差公式。山第一节可知,对于交替标志: X=p on=pq 根据抽样平均误差与总体标准差平方之间的关系,抽样成数的半均误差计算公式为: 重复抽样抽样数的半均误差4,,P0卫 个复指样地传成的约装法,P1一习 在上面计算抽样平均误差的公式中,无论是平均数的标准差。,还是交替标志的方差 P1一P),都是指全及总体而言。但是在抽样调查的实践中,这两个指标一般都是未知的, 因此,通常采用以下四种方法米解决。 ()用过去调查所得到的资料。可以用全面调查的资料,也可以用抽样调查的资料。 如果有几个不同的总体方差的资料,则应该用数值较大的。 (2)用样本方差的资料代替总体方差。概率论的研究从理论上作了证明,样本方差可以 相当接近于总体方差。这是实际工作中经常使用的一种方法,但它只能在调查之后才能计算 (3)用小规模调查资料。如果既没有过去的材料,又需要在调查之前就估计出抽样误差, 实在不得已时,可以在大规模调查之前,组织一次小规模的试验性训查。 (4)用估计的材料。例,在农产量抽样调查中用农产量预计估产的资料,根据预计