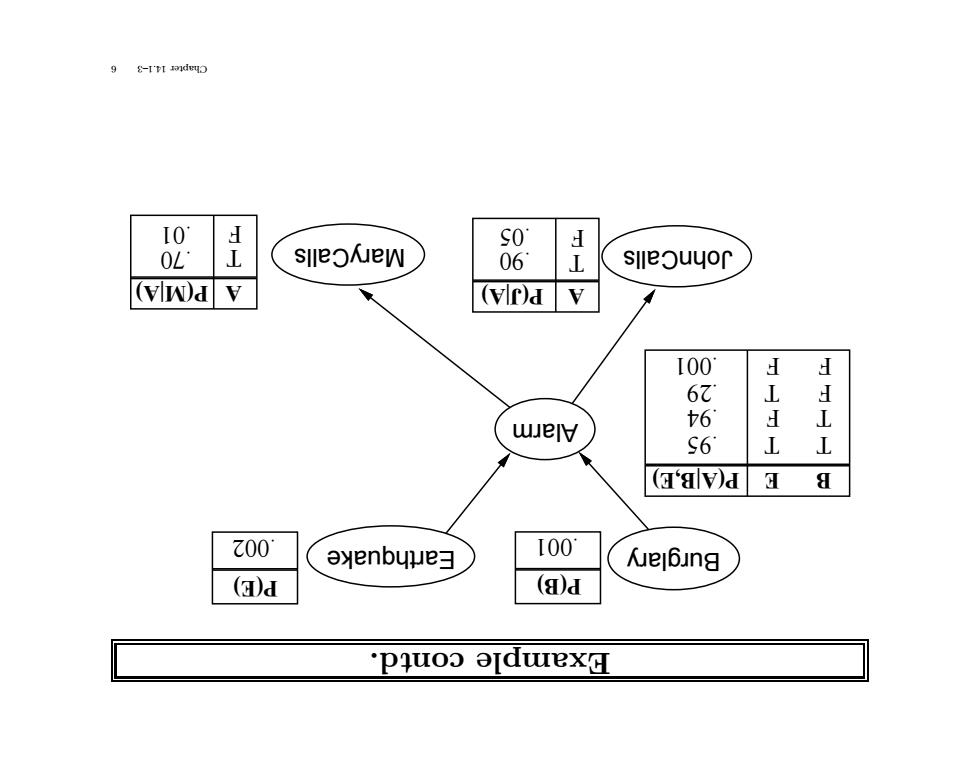
9 $-I'I anduD IO SO OL slleoeW 06 L slleouyor (vw)dv (vIr)av [00 d d 67 L d 6 wely L s6 L L (alvda a Z00 ayenbμe] I00 人ue6na (3a (aJ pquoo aldwexH
td. con Example .001 P(B) .002 P(E) Alarm Earthquake MaryCalls JohnCalls Burglary B T T F F E T F T F .95 .29 .001 .94 P(A|B,E) A T F .90 .05 A P(J|A) T F .70 .01 P(M|A) 6 14.1–3 Chapter
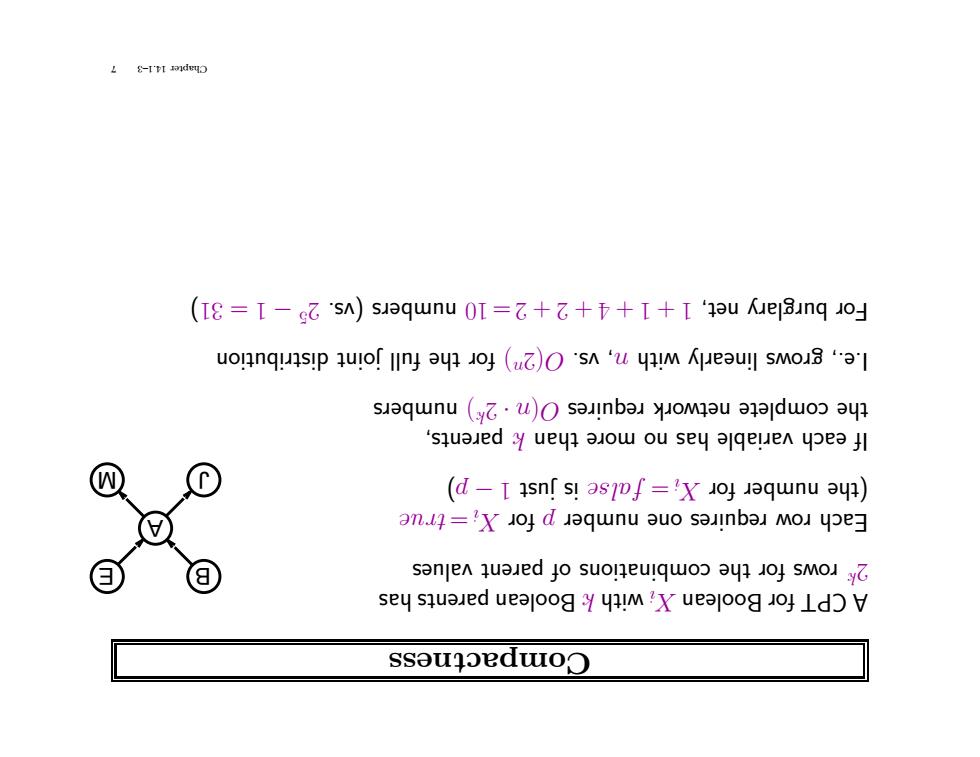
上8-I'PI d3 (I8=I-gZsA)sjeqwnu0I=乙+乙+币+I+I'au Ke]3unq Jo」 uonnquas!p quof lIng ayn oj 'sA 'u yim Kjeau!l sMo3 "l s3qunu(y乙·u)Os31nb31Ho4au341duoa44 'squaued y ueyn ajow ou sey ajqeuen yoea Jl (d-I isnf s!as of='x joj jaqwnu ay) an.l='x oj d jaqwnu auo sauinba mou ype S3 njen qualed0suoI4 eulqwo)∂y1 o]SMO1.y乙 sey squaed ueajoog y ylm'X ueajoog oj Ld)y ssouyoedwoD
Compactness has rents pa olean Bo k with i X olean Bo r fo CPT A E B J A M 2k values rent pa of combinations the r fo ws ro ue tr =i Xr fo p er numb one requires wro Each ) p −1 just is se al f =i Xr fo er numb (the rents, pa k than re mo no has riable va each If 2· n( O requires rk ow net complete the k ers numb ) (2 O vs. , n with rly linea ws gro I.e., n distribution joint full the r fo ) 2 (vs. ers numb 10 =2 +2 +4 +1 +1 net, ry burgla r oF −5 ) 31 =1 7 14.1–3 Chapter
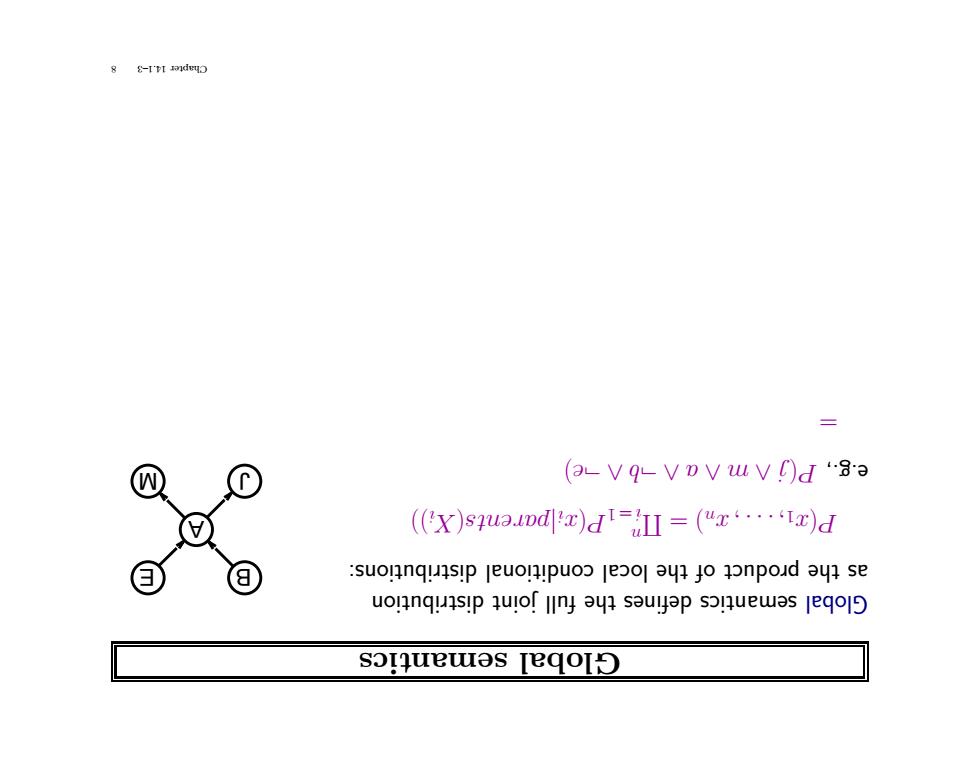
8 $-I'I anduyD = (aVq-vovwvr)da ((x)squaud)d=(ux)d :suolinq!sip jeuon!puoo jeool ay1 jo aonpod ayn se uolnqunsip quiof lIny ayn sauyap soluewas leqo]5 sorquewas jeqol
tics seman Global distribution joint full the defines semantics Global E B J A M distributions: conditional cal lo the of duct ro p the as Π =)n x, . . . , 1 x( P n P1 =i )) i X( ents par |i x( )e ¬ ∧b ¬ ∧a ∧ m∧j( P e.g., = 8 14.1–3 Chapter
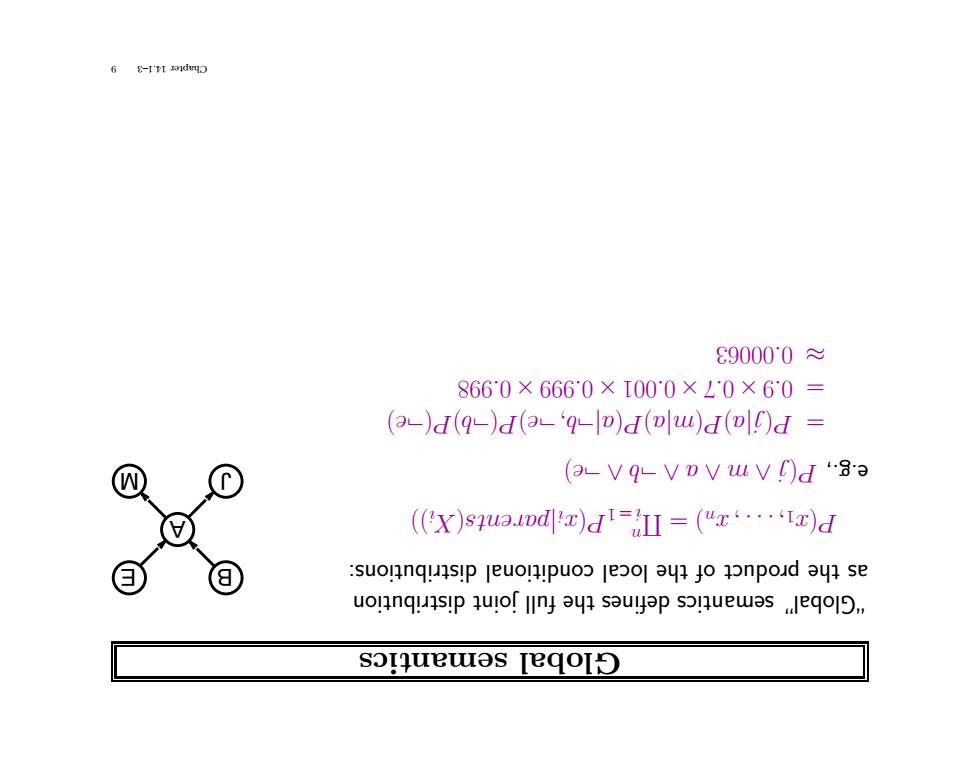
6 8-1'VI 890000≈ 8660×6660×I000×ㄥ0×60= (3)d(q-)d(aq-)d(w)d(!)d (a-Vq-vovwv)d "83 ((x)squaud)d==(")d :suolnq!sip leuon!puoo jeool ay]yo aonpoud ayl se uolnqunsip quiof lny ay sauyap sonuewas eqo]9, somquewas [eqol
tics seman Global distribution joint full the defines semantics “Global” E B J A M distributions: conditional cal lo the of duct ro p the as Π =)n x, . . . , 1 x( P n P1 =i )) i X( ents par |i x( )e ¬ ∧b ¬ ∧a ∧ m∧j( P e.g., )e ¬( P)b ¬( P)e ¬ b, |¬a( P) a| m( P) a| j( P = 998 . 0 × 999 . 0 × 001 . 0 ×7. 0 ×9. 0 = 00063 . 0 ≈ 9 14.1–3 Chapter
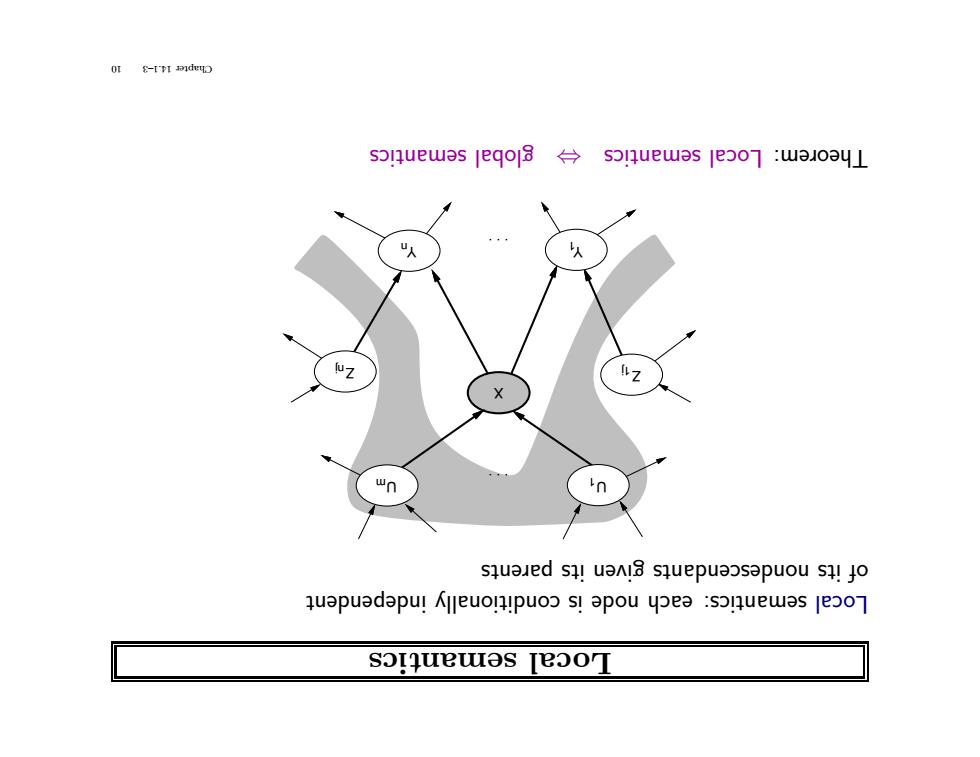
0I名-I'PI deD sonuewas eqo3 sonuewas jeo]:wajoay squaed sil uanlg squepuaosapuou si!jo quapuadapul Kjleuonlpuoo sl apou yoea soIuewas e5o] sorquewas jeoor
tics seman cal Lo endent indep conditionally is de no each semantics: cal Lo rents pa its given nondescendants its of . . . . . . 1 U X mU nY nj Z 1Y 1j Z semantics global ⇔ semantics cal Lo rem: Theo 10 14.1–3 Chapter