
心号与事我 m4.13 §4.12拉普拉斯变换与傅里叶变 换的关系 米 新疆大学信息科学与工程学院电子系 2011.1 退出 开始
新疆大学信息科学与工程学院电子系 2011.1 §4.12 拉普拉斯变换与傅里叶变 换的关系 4.13

引言 我们在引出拉氏变换时,是针对f()不满足绝对 可积条件,对其乘以一个衰减因玉,作傅氏变换 演变为拉氏变换 [fl=Fy0e'小=Fs)n 由此可以得到傅氏变换与拉氏变换的关系 当o。>0时,收敛边界落右半平面 当σ。<0时,收敛边界落于玉左半平面 当σ。=0时,收敛边界位于虚轴
X 第 2 页 ( ) 演变为拉氏变换 可积条件 对其乘以一个衰减因子 作傅氏变换 我们在引出拉氏变换时 是针对 不满足绝对 , e , , , t f t − ( ) ( ) e ( ) ( ) s σ jω σ t L f t F f t u t F s = + − = = 由此可以得到傅氏变换与拉氏变换的关系 当σ0 0时,收敛边界落于s 右半平面 当σ0 0时,收敛边界落于s左半平面 当σ0 = 0时,收敛边界位于虚轴 引言
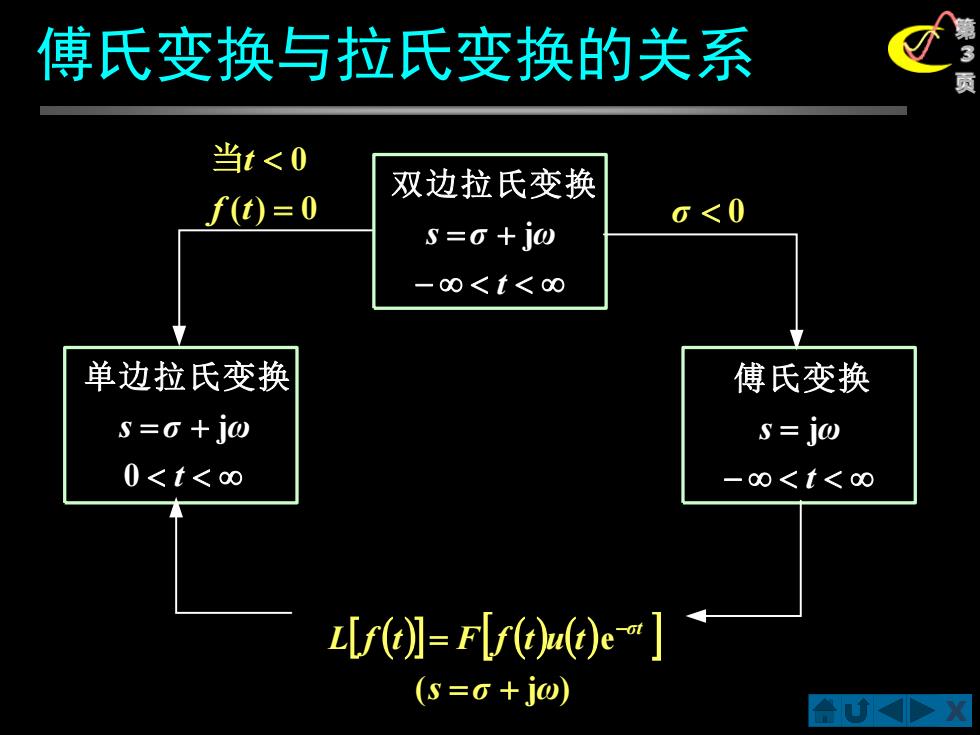
傅氏变换与拉氏变换的关系 当t<0 双边拉氏变换 f(t)=0 0<0 S=o+jω -0<t<0 单边拉氏变换 傅氏变换 S=0+jω S=jω 0<t<o -0<t<0 L[r】=Frt)d)e"] (s=0+j@)
X 第 3 傅氏变换与拉氏变换的关系 页 − = + t s σ jω 双边拉氏变换 − = t s jω 傅氏变换 = + t s σ ω 0 j 单边拉氏变换( ) 0 0 = f t 当t σ 0 ( ) ( ) ( ) ( j ) e s σ ω L f t F f t u t σt = + = −
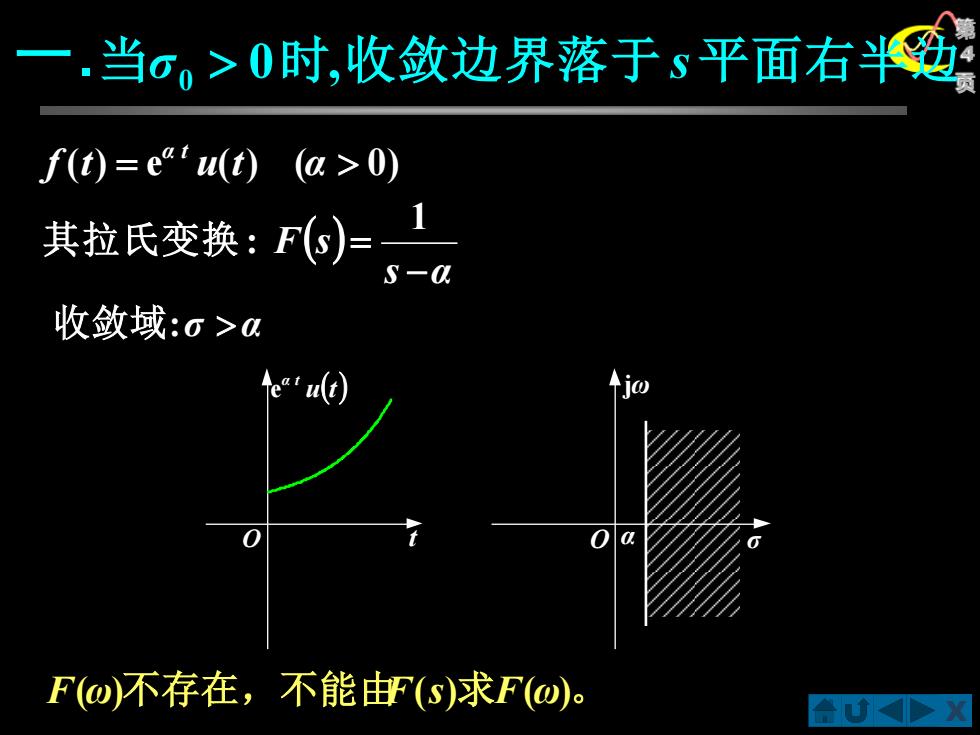
一.当σ。>0时,收敛边界落于s平面右半劲 f(t)=e&'(t)(a>0) 其拉氏变换:F(S)= S- 收敛域:o>a e"'ult 0 F(@不存在,不能由(s)求F@)
X第4 一. 页 O σ jωα 当 σ 0 0 时,收敛边界落于 s平面右半边 f ( t ) = e u ( t ) (α 0 ) α t ( ) s α F s − = 1 其拉氏变换 : F(ω)不存在,不能由F ( s ) 求F (ω ) 。 收敛域 : σ α O t u (t ) α t e
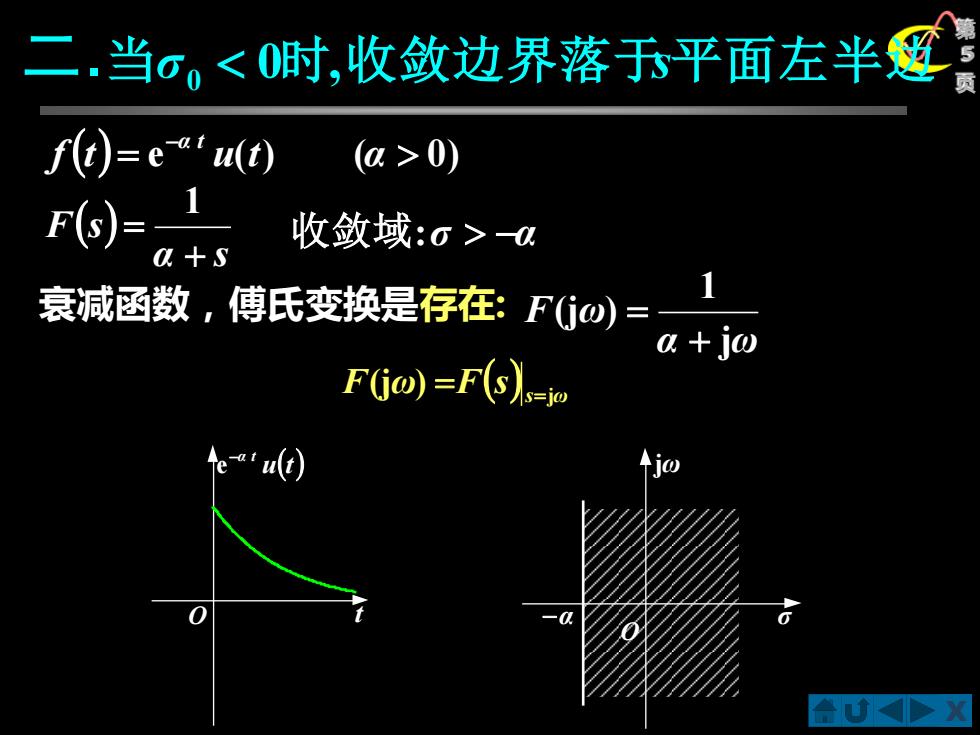
二.当σ。<0时,收敛边界落玉平面左半班 f(t)=e"u(t) (a>0) 收敛域:σ>a 衰减函数,傅氏变换是存在:Fo)= a +jo F(jo)=F(s)
X 第 5 二. 页 O σ jω O t −α u(t) −α t e 当σ0 0时,收敛边界落于s平面左半边 ( ) = e ( ) ( 0) − f t u t α α t 衰减函数,傅氏变换是存在: ( ) 1 α s F s + = j 1 (j ) α ω F ω + = 收敛域:σ −α ( )s ω F ω F s j (j ) = =