
飞号与事型 §4.7由系统蓝数零、极点分布决 定时域特性 言 Hs零极点与h①波形特征 Hs)、Es的极点分布与自由响 应、强迫响应特性的对应 新疆大学信息科学与工程学院电子米 2011.1 退出 开始
新疆大学信息科学与工程学院电子系 2011.1 §4.7 由系统函数零、极点分布决 定时域特性 • 序言 • H(s)零、极点与h(t)波形特征 • H(s) 、E(s)的极点分布与自由响 应、强迫响应特性的对应

序言 冲激响应(①与系统函数H(s)从时域和变换域两方 面表征了同一系统的本性。 在域分析中,借助系统函数在s平面零点与极点 分布的研究,可以简明、直观地给出系统响应的许多 规律。系统的时域、频域特性集中地以其系统函数的 零、极点分布表现出来。 主要优点: 1.可以预言系统的时域特性; 2.便于划分系统的各个分量 (自由/强迫,瞬态/稳态); 3.可以用来说明系统的正弦稳态特性。 合UD
X 第 2 一.序言 页 冲激响应h(t)与系统函数H(s) 从时域和变换域两方 面表征了同一系统的本性。 在s域分析中,借助系统函数在s平面零点与极点 分布的研究,可以简明、直观地给出系统响应的许多 规律。系统的时域、频域特性集中地以其系统函数的 零、极点分布表现出来。 主要优点: 1.可以预言系统的时域特性; 2.便于划分系统的各个分量 (自由/强迫,瞬态/稳态); 3.可以用来说明系统的正弦稳态特性

二. H(S)零、极点与h()波形特征的袋 1.系统函数的零、极点 H=4)=K-名s-).6-2).s-n) B(s) (S-p(S-p2).(S-Pk).(S-pn) 乙1,32.乙n =I i=1 系统函数的零点 Πs-p) D1,p2··pn k 系统函数的极点 在s平面上,画出H(s的零极点图: 极点:用×表示,零点:用表示 刨题 合U>风
X 第 3 二.H(s)零、极点与h(t)波形特征的对应页 ( )( ) ( ) ( ) ( )( ) ( ) ( ) ( ) ( ) ( ) 1 2 1 2 k n j m s p s p s p s p s z s z s z s z K B s A s H s − − − − − − − − = = = K 系统函数的零点 , 1 2 n z z z 系统函数的极点 , p1 p2 pn 在s平面上,画出H(s)的零极点图: 极点:用×表示,零点:用○表示 = − m j j s z 1 ( ) = − n k k s p 1 ( ) 1.系统函数的零、极点
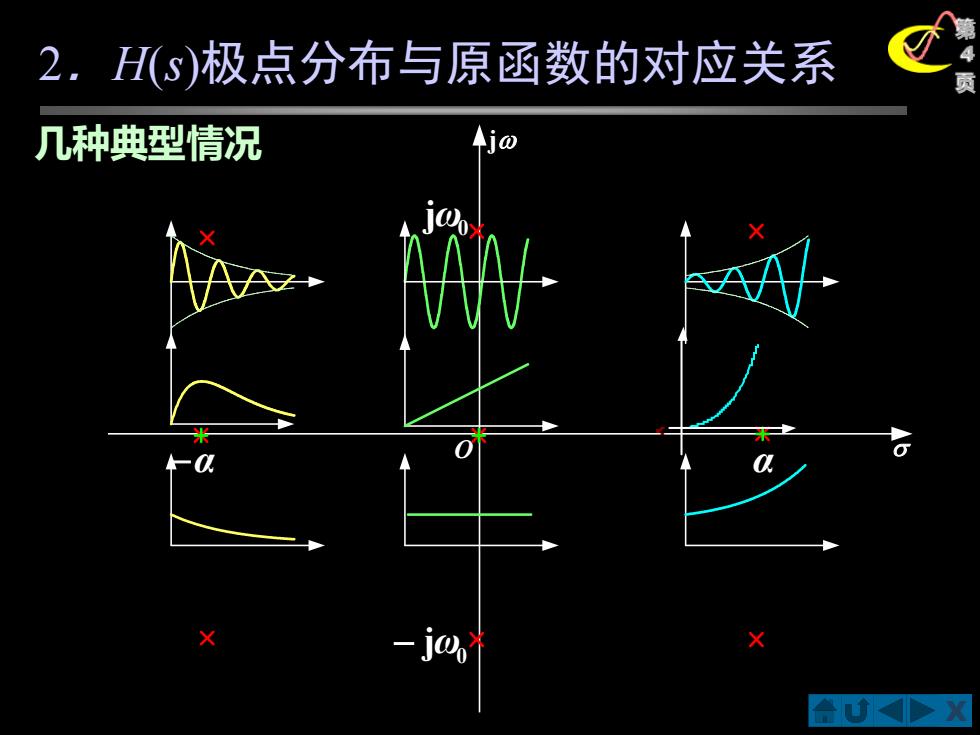
2.H(s)极点分布与原函数的对应关系 几种典型情况 -j0 合UD
X 第 4 2.H 页 (s)极点分布与原函数的对应关系 j O −α α 0 jω 0 − jω 几种典型情况

阶极点 1 H(S)=-, P1=0在原点,h(t)=H(s川=u() H(s)=s+a' P1=-0 a>0,在左实轴上,h(t)=eu(t),指数衰减 a<0,在右实轴上,h(t)=e(t),-a>0,指数增加 0 Hs)=g+0) 卫=jo,在虚轴上 h(t)=sinotu(t),等幅振荡 H(S)= ω s+a)2+o2’B=a+jm,pP,=a-jo,共轭根 当α>0,极点在左半平面,衰减振荡 当α<0,极点在右半平面,增幅振荡
X 第 5 一阶极点 页 , 0在原点, 1 ( ) = p1 = s H s ( ) [ ( )] ( ) 1 h t = L H s = u t − p a s a H s = − + = 1 , 1 ( ) 0, , ( ) e ( ), 0, 0, , ( ) e ( ), 在右实轴上 指数增加 在左实轴上 指数衰减 = − = − − a h t u t a a h t u t a t a t ( ) 2 2 , p1 jω,在虚轴上 s ω ω H s = + = h(t) = sinωtu(t),等幅振荡 , ( ) ( ) 2 2 s α ω ω H s + + = p1 = −α + jω, p2 = −α − j,共轭根 当 ,极点在左半平面,衰减振荡 当 ,极点在右半平面,增幅振荡 α 0 α 0