
心号与事我 §5,9从抽样信号恢复 连续时间信号 由抽样信号恢复原信号 零阶抽样保持 头 新疆大学信息科学与工程学院电子系 2003.1 退出 开始
新疆大学信息科学与工程学院电子系 2003.1 § 5.9 从抽样信号恢复 连续时间信号 •由抽样信号恢复原信号 •零阶抽样保持

由抽样信号恢复原信号 理想低通滤波器 个Fs(o) 0s>20 H0)- w>o. O0m F(@)=F(@)H(o)fd)=fd)*t) 滤除高频成分,即可恢复原信号 -0c00c F@ 从时域运算解释 -000m 0 合U
X 第 2 页 理想低通滤波器 滤除高频成分,即可恢复原信号 ( ) = c s c 0 T H F( ) = F ( ) H( ) f (t) = f (t)h(t) s s 一.由抽样信号恢复原信号 o H() − C C TS o F() − m m 1 o () FS S 1 T −S m S S − m S 2 m 从时域运算解释

时域运算 以理想抽样为例 时域:f)=f)6,(0)=∑f(nT)5t-nT) 1=-c0 缬域:Fo)=2 F)-P(w=)2ro-na) 理想低通滤波器 o>0 时球:h0=r2so,动 0=a-28-:gs®,) =T9∑fnI)sa@.i-nr)】 元
X 第 3 时域运算 页 以理想抽样为例 =− = = − n f (t) f (t) (t) f (nT ) (t nT ) 时域: s T s s ( ) ( ) ( ) ( ) =− = = − n F n T F F P s S s 1 2π 1 频域: 理想低通滤波器: ( ) = c s c 0 T 频域:H h(t) T ( t) c c s Sa π 时域: = ( ) ( ) ( ) = = − =− f t f t h t f nT t nT T t n c c s s s s Sa π ( ) ( ) ( ) ( ) s c s c s ( )Sa π T f nT t nT n = − =−

说明 r()=nruT)salo.(-nT)] =-00 连续信号f)可以展开成Sa函数的无穷级数,级数的系 数等于抽样值fnTs)。 ·也可以说在抽样信号f①)的每个抽样值上画一个峰值 为fnT)的Sa函数波形,由此合成的信号就是)。 当0,=20m’则有0.=0m,T、= 2π 元 此时r0)=ΣfnI)sa[o.k-mI)] 演示
X 第 4 页 • 连续信号f(t)可以展开成Sa函数的无穷级数,级数的系 数等于抽样值f(nTs )。 • 也可以说在抽样信号fs (t)的每个抽样值上画一个峰值 为f(nTs ) 的Sa函数波形,由此合成的信号就是fs (t) 。 s c m c m s 2π π 2 , 当s = ,则有 = T = = ( ) ( ) s Sa c s f t f (nT ) t nT n = − =− 此 时 ( ) ( ) s c s c s ( )Sa π f t T f nT t nT n = − =− 说明
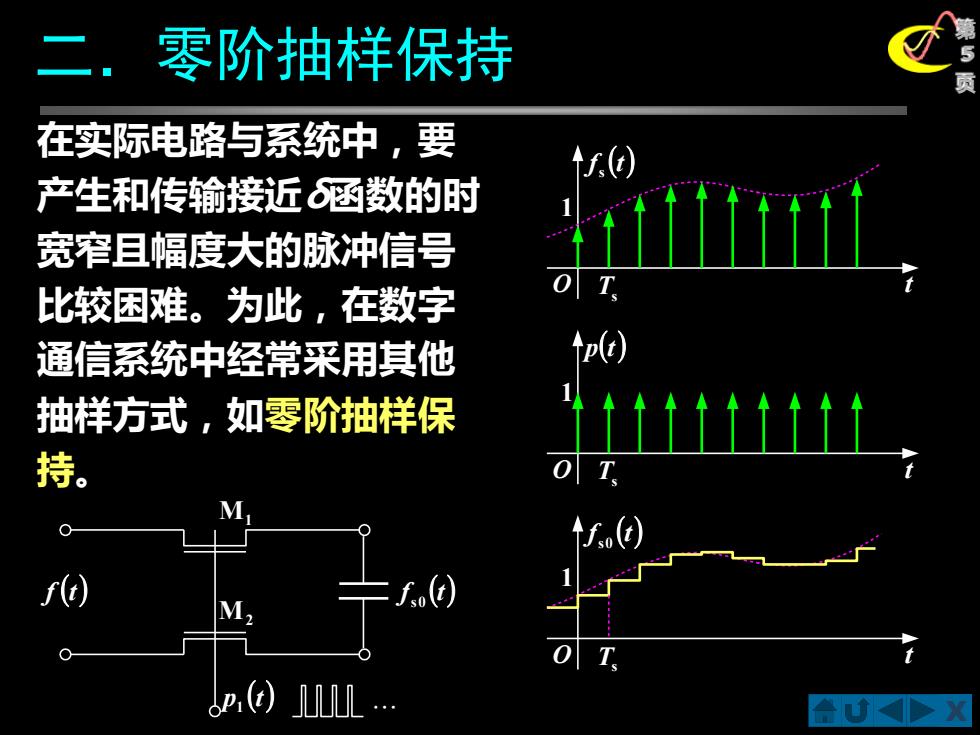
二.零阶抽样保持 在实际电路与系统中,要 产生和传输接近6涵数的时 宽窄且幅度大的脉冲信号 比较困难。为此,在数字 通信系统中经常采用其他 ↑pd 抽样方式,如零阶抽样保 tttttttt 持。 r(t M
X 第 5 二.零阶抽样保持 页 M1 M2 f (t) f (t) s0 p (t) 1 在实际电路与系统中,要 产生和传输接近δ函数的时 宽窄且幅度大的脉冲信号 比较困难。为此,在数字 通信系统中经常采用其他 抽样方式,如零阶抽样保 持。 O f (t) s t 1 O f (t) s0 t 1 Ts Ts O p(t) t 1 Ts